Магнитное поле, создаваемое токами проводимости (макротоками) в среде, отличается от магнитного поля в вакууме. Это изменение связано с взаимодействием магнитного поля с веществом, в результате которого вещество намагничивается и приобретает магнитный момент. Причиной намагничивания является существование молекулярных токов. Еще в 1820 г. Ампер высказал гипотезу о существовании элементарных круговых токов в веществе. Природа элементарных токов стала понятна и гипотеза подтвердилась, когда было установлено, что атом состоит из ядра и движущихся вокруг электронов по модели атома Резерфорда.1
В классической физике электрон е, обращающийся вокруг ядра по орбите радиусом r, с частотой n, эквивалентен круговому току I и обладает орбитальным магнитным моментом

где  – сила тока;
– сила тока; 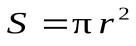 – площадь орбиты;
– площадь орбиты;  – единичная нормаль к плоскости орбиты.
– единичная нормаль к плоскости орбиты.
Также движущийся по орбите электрон обладает механическим моментом импульса 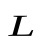 , называемым орбитальным, величина которого равна
, называемым орбитальным, величина которого равна
 .
.
Векторы 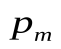 и
и 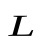 направлены противоположно, и их отношение
направлены противоположно, и их отношение

называется гиромагнитным отношением.
В 1915 г. Эйнштейн1 и де Гааз2 установили, что экспериментальное значение гиромагнитного отношения в два раза больше и равно:
 .
.
Для объяснения полученного результата они предположили, что, помимо орбитальных моментов, электрон обладает собственным механическим моментом импульса  , названным спином, и собственным спиновым магнитным моментом
, названным спином, и собственным спиновым магнитным моментом  . Именно их отношение и равно
. Именно их отношение и равно  . Это предположение впоследствии подтвердилось.
. Это предположение впоследствии подтвердилось.
Таким образом, электрон в атоме обладает орбитальным магнитным моментом 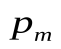 и спиновым магнитным моментом
и спиновым магнитным моментом  . Зная число электронов в атоме, их расположение и взаимодействие, можно определить магнитный момент
. Зная число электронов в атоме, их расположение и взаимодействие, можно определить магнитный момент  атома.
атома.
В простейшем случае  вычисляют в виде векторной суммы орбитальных и спиновых магнитных моментов электронов атома:
вычисляют в виде векторной суммы орбитальных и спиновых магнитных моментов электронов атома:
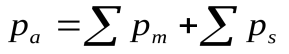 .
.
Магнитным моментом ядра атома пренебрегают, ввиду его малости.
Благодаря магнитным моментам атомов любое вещество обладает магнитными свойствами и является магнетиком. Под действием магнитного поля магнетик намагничивается. Намагничивание вещества характеризует вектор  , называемый намагниченностью вещества и равный магнитному моменту единицы объема магнетика:
, называемый намагниченностью вещества и равный магнитному моменту единицы объема магнетика:
 ,
,
где V – физически малый объем.
Намагниченность характеризует магнитное состояние вещества. В системе СИ намагниченность измеряется в [ I ] = 1 А/м.
Поле в магнетике. Всякое вещество является магнетиком, т.е. способно намагничиваться -приобретать магнитный момент. Если внести магнетик в магнитное поле с индукцией  , то результирующее поле
, то результирующее поле  будет векторной суммой вектора
будет векторной суммой вектора  и собственного поля магнетика
и собственного поля магнетика  :
:
 =
=  +
+  . (83)
. (83)
Вектор  не имеет специальных источников, поэтому для поля
не имеет специальных источников, поэтому для поля  в магнетике справедлива
в магнетике справедлива
теорема Гаусса: Поток вектора  сквозь любую замкнутую поверхность равен нулю:
сквозь любую замкнутую поверхность равен нулю:
 . (84)
. (84)
Это значит, что линии вектора  и при наличии вещества остаются непрерывными. Природа магнитных свойств вещества может быть полностью обоснована методами квантовой механики, а в электродинамике можно ограничиться следующими модельными представлениями. Молекулы многих веществ обладают магнитными моментами, обусловленными движением заряженных частиц внутри молекул. В отсутствие внешнего магнитного поля магнитные моменты молекул ориентированы беспорядочно, поэтому результирующее поле внутри магнетика равно нулю. Если при отсутствии внешнего поля молекулы не обладают магнитными моментами, то внесении поле в молекулах возникают индуцированные круговые токи, в результате чего сами молекулы и вместе с ними и все вещество приобретает магнитный момент и соответствующее собственное поле магнетика
и при наличии вещества остаются непрерывными. Природа магнитных свойств вещества может быть полностью обоснована методами квантовой механики, а в электродинамике можно ограничиться следующими модельными представлениями. Молекулы многих веществ обладают магнитными моментами, обусловленными движением заряженных частиц внутри молекул. В отсутствие внешнего магнитного поля магнитные моменты молекул ориентированы беспорядочно, поэтому результирующее поле внутри магнетика равно нулю. Если при отсутствии внешнего поля молекулы не обладают магнитными моментами, то внесении поле в молекулах возникают индуцированные круговые токи, в результате чего сами молекулы и вместе с ними и все вещество приобретает магнитный момент и соответствующее собственное поле магнетика  . Большинство магнетиков намагничиваются слабо. Сильными магнитными свойствами обладают только железо, никель, кобальт и многие их сплавы.
. Большинство магнетиков намагничиваются слабо. Сильными магнитными свойствами обладают только железо, никель, кобальт и многие их сплавы.
Установим связь между основной ( ) и вспомогательной (
) и вспомогательной ( ) характеристиками магнитного поля.
) характеристиками магнитного поля.
Как показывает опыт, в неслишком сильных магнитных полях для однородного изотропного магнетика вектор намагниченности пропорционален напряженности поля, т.е.
 (13.11)
(13.11)
где  («хи») – магнитная восприимчивость магнетика (безразмерная величина, характеризующая способность вещества к намагничиванию). Для однородных изотропных магнетоков
(«хи») – магнитная восприимчивость магнетика (безразмерная величина, характеризующая способность вещества к намагничиванию). Для однородных изотропных магнетоков  не зависит от
не зависит от  .
.
Подставив (13.11) в (13.8), получим

откуда
 (13.12)
(13.12)
Безразмерная величина, стоящая в (13.12) в скобках, то есть
 (13.13)
(13.13)
называется магнитной проницаемостью  вещества.
вещества.
Таким образом, напряженность и индукция магнитного поля связаны соотношениями:
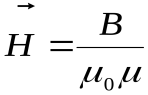 или
или  . (13.14)
. (13.14)
Для вакуума  =1, поэтому снова приходим к соотношению (13.9).
=1, поэтому снова приходим к соотношению (13.9).
Выясним физический смысл магнитной проницаемости вещества. Для этого умножим равенство (13.10) на  :
:
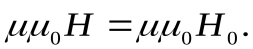
Преобразовав это соотношение с учетом (13.14) и (13.9), получим
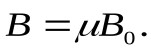 (13.15)
(13.15)
Следовательно, магнитная проницаемость  показывает, во сколько раз внешнее магнитное поле
показывает, во сколько раз внешнее магнитное поле 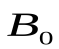 изменяется за счет магнетика.
изменяется за счет магнетика.