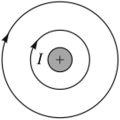
Рис. 22.4
Построим картину линий напряженности магнитного ноля вокруг бесконечного прямолинейного проводника с током (рис. 22.4). По аналогии с циркуляцией вектора напряженности электростатического поля (17.7) введем понятие циркуляции вектора напряженности магнитного
ПОЛЯ'.
Для простоты сначала в качестве контура выберем окружность, совпадающую с одной из линий напряженности магнитного поля. В соответствии с формулой (22.12) напряженность на этой окружности является константой. А в соответствии с рис. 22.4 вектор напряженности направлен но касательной к окружности. Эти соображения позволяют вычислить циркуляцию:
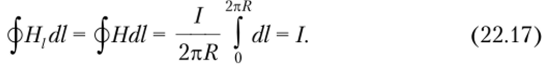Принцип суперпозиции магнитных полей и рассуждения, аналогичные предпринятым в разделе о циркуляции вектора напряженности электростатического поля, позволяют обобщить полученное выражение на несколько токов и произвольный контур:
Это и есть теорема о циркуляции вектора напряженности магнитного поля: циркуляция вектора напряженности магнитного поля по произвольному контуру равна алгебраической сумме токов, охватываемых контуром.
Теперь домножением обеих частей уравнения (22.18) на р0ц получим теорему о циркуляции вектора магнитной индукции:
Искусство применения теоремы о циркуляции состоит в выборе удобного для расчета контура.
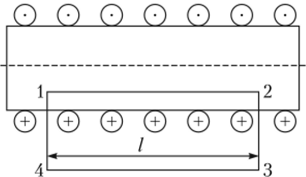Рис. 22.5
Применим теорему о циркуляции для вычисления напряженности магнитного поля длинного соленоида с током I. Соленоид — это провод, равномерно навитый на цилиндрический каркас (рис. 22.5). Будем считать, что диаметр каркаса много меньше его длины, а шаг плотной намотки (расстояние между витками) много меньше диаметра. При этих условиях поле внутри соленоида, как будет очевидно из результата, много больше поля вне соленоида и достаточно однородно (заметим, что поле вне соленоида можно определить по формуле для магнитного поля прямого тока (22.12)). Из соображений симметрии поле внутри соленоида направлено вдоль оси соленоида. Пусть плотность намотки витков (количество витков на единицу длины каркаса) равна п витков на метр.
В соответствии с рис 22.5 выберем прямоугольный контур, у которого малые (по сравнению с большими сторонами длиной /) стороны 2—3 и 4—1 в точке протыкания каркаса перпендикулярны каркасу, большая сторона 1—2 находится внутри каркаса, большая сторона 3—4 находится вне каркаса. В такой ситуации в циркуляции, состоящей из четырех интегралов по отрезкам, доминирует составляющая по отрезку 1—2. Составляющими по отрезкам 2—3 и 4—1 можно пренебречь вследствие малости отрезков. Составляющей по отрезку 3—4 можно пренебречь вследствие перпендикулярности (приблизительно) поля отрезку и малости этого поля. Внутрь контура попадает п! витков с током. Таким образом, циркуляция сводится к отрезку 1—2, но в соответствии с формулой (22.19) определяется полным током nil внутри контура:
 
Отметим, что это поле достаточно однородно по диаметру каркаса, ведь стороны 2—3 и 4— 1 малы лишь по сравнению с длиной каркаса, но могут быть сравнимы с диаметром каркаса и углубляться внутрь каркаса на любое расстояние.
Соответственно, магнитная индукция внутри длинного соленоида равна
 
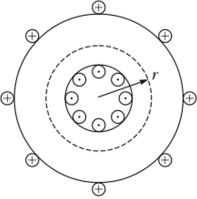Рис. 22.6
19. Поток вектора напряженности магнитного поля (магнитной индукции). Теорема Гаусса для магнитного поля.
|
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна 
(1) где Bn=Вcosα - проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), d S =dS n — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции ФB через произвольную заданную поверхность S равен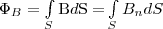 
(2) Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В, Bn=B=const и 
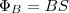Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м2, который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м2). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: 
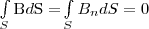(3) Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Следовательно, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы. В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна 
Магнитный поток сквозь один виток соленоида площадью S равен 
а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением, 