Пьезоэлектрический эффект

Изучение свойств твердых диэлектриков показало, что некоторые из них поляризуются не только с помощью электрического поля, но и в процессе деформации при механических воздействиях на них.

Поляризация диэлектрика при механическом воздействии на него называется прямым пьезоэлектрическим эффектом. Этот эффект присущ кристаллам кварца и всем сегментоэлектрикам. Чтобы его наблюдать, из кристалла вырезают прямоугольный параллелепипед, грани которого должны быть ориентированы строго определенным образом относительно кристалла. При сдавливании параллелепипеда одна его грань заряжается положительно, а другая - отрицательно. Оказывается, что в этом случае плотность поляризационного заряда грани прямо пропорциональна давлению и не зависит от величины параллелепипеда. Если сжатие заменить растяжением параллелепипеда, то заряды на его гранях изменят знаки на обратные.

У пьезокристаллов наблюдается и обратное явление. Если пластинку, вырезанную из пьезокристалла, поместить в электрическое поле, зарядив металлические обкладки, то она поляризуется и деформируется, например сжимается. При перемене направления внешнего электрического поля сжатие пластинки сменяется ее растяжением (расширением). Такое явление называется обратным пьезоэлектрическим эффектом.

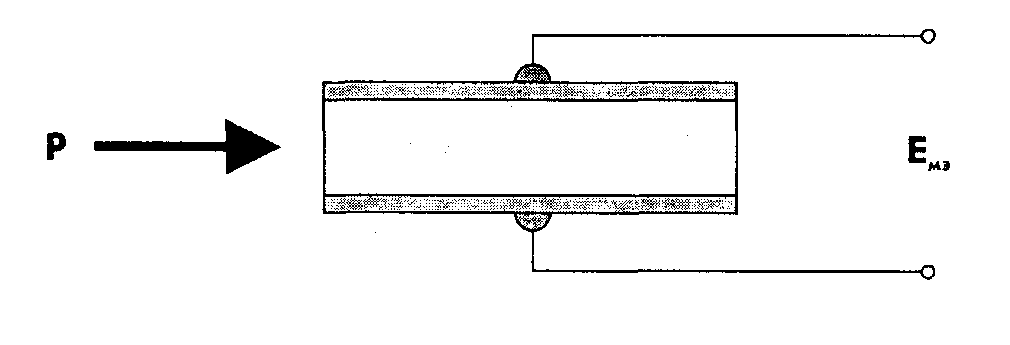
Рис. 31. Пьезоэлектрический преобразователь

Чтобы воспринять изменение заряда или напряжения, к пьезоэлектрическому материалу подсоединяют две металлические пластины, фактически образующие пластины конденсатора, емкость которого определяется соотношение

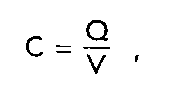
мгде Q - заряд,

V - напряжение.

На рис. 31 приведено устройство пьезоэлектрического преобразователя.

На практике в качестве пьезоэлектрического материала применяются кристаллы кварца, рочелиевая соль, синтетические кристаллы (сульфат лития) и поляризованная керамика (титана бария).

Кварцевые пластины широко используются в пьезоэлектрических микрофонах, охранных датчиках, стабилизаторах генераторов незатухающих колебаний.

На рис. 32 показано устройство пьезоэлектрического микрофона

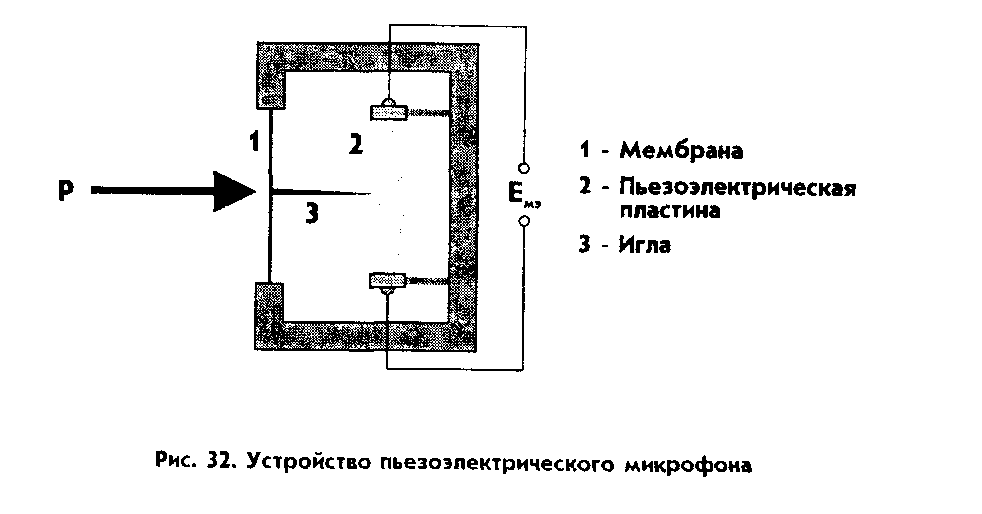
. Когда звуковое давление отклоняет диафрагму, ее движение вызывает деформацию пьезоэлектрической пластины, которая в свою очередь вырабатывает электрический сигнал на выходных контактах.

Проводники в электростатическом поле. Электроемкость уединенного проводника. Конденсаторы. Электроемкость конденсатора. Энергия проводника и конденсатора. Энергия электростатического поля.

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действо­вать электростатическое поле, в результа­те чего они начнут перемещаться. Переме­щение зарядов (ток) продолжается до тех пор, пока не установится равновесное рас­пределение зарядов, при котором электро­статическое поле внутри проводника обра­щается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напря­женность поля во всех точках внутри проводника равна нулю:

Е==0.

Отсутствие поля внутри проводника означает, согласно (85.2), что потенциал во всех точках внутри проводника постоя­нен (j=const), т.е. поверхность провод­ника в электростатическом поле является эквипотенциальной (см. §85). Отсюда же

следует, что вектор напряженности поля на внешней поверхности проводника направ­лен по нормали к каждой точке его по­верхности. Если бы это было не так, то под действием касательной составляющей Е заряды начали бы по поверхности про­водника перемещаться, что, в свою оче­редь, противоречило бы равновесному рас­пределению зарядов.

Если проводнику сообщить некоторый заряд Q, то нескомпенсированные заряды располагаются только на поверхности про­водника. Это следует непосредственно из теоремы Гаусса (89.3), согласно которой заряд Q, находящийся внутри проводника в некотором объеме, ограниченном про­извольной замкнутой поверхностью, равен

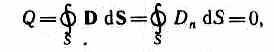
так как во всех точках внутри поверхности D=0.

Найдем взаимосвязь между напряжен­ностью Е поля вблизи поверхности заря­женного проводника и поверхностной плотностью а зарядов на его поверхности. Для этого применим теорему Гаусса к бес­конечно малому цилиндру с основаниями AS, пересекающему границу проводник — диэлектрик. Ось цилиндра ориентирована вдоль вектора Е (рис. 141). Поток вектора электрического смещения через внутрен­нюю часть цилиндрической поверхности равен нулю, так как внутри проводника e ₁ (а следовательно, и d ₁) равен нулю, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяет­ся только потоком сквозь наружное осно­вание цилиндра. Согласно теореме Гаусса (89.3), этот поток (DDS) равен сумме за-

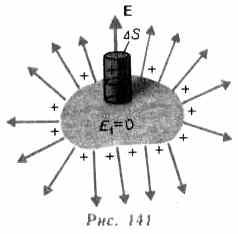
рядов (Q=sDS), охватываемых поверхно­стью: DDS=sDS, т. е.

D=s (92.1)

или

E =s/(e₀e), (92.2)

где e — диэлектрическая проницаемость среды, окружающей проводник.

Таким образом, напряженность элек­тростатического поля у поверхности про­водника определяется поверхностной плотностью зарядов. Можно показать, что соотношение (92.2) задает напряженность электростатического поля вблизи поверх­ности проводника любой формы.

Уединенным называется проводник, вблизи которого нет других заряжен­ных тел, диэлектриков, которые могли бы повлиять на распределение зарядов дан­ного проводника.

Отношение величины заряда к потенциалу для конкретного проводника есть величина постоянная, называемая электроемкостью (емкостью) С, .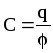

Таким образом, электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потен­циал на единицу. Опыт показал, что электроемкость уединенного проводника зависит от его гео­метрических размеров, формы, диэлектрических свойств окружающей среды и не за­висит от величины заряда проводника.

Электроёмкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между этим проводником и соседним.

Электроёмкость обозначается буквой 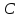, вычисляется по формул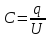е: где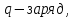

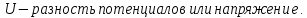
Единица измерения электроёмкости: Фарад (Ф).

Конденсатор представляет собой два проводника, разделённые слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Электроёмкость конденсатора определяется формулой: .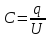

Конденсаторы бывают разных видов: бумажные, слюдяные, воздушные и т.д. по типу используемого диэлектрика.

Также бывают конденсаторы постоянной и переменной электроёмкости.

Электроёмкость конденсатора зависит от вида диэлектрика, расстояния между пластинами и площади пластин: 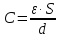, где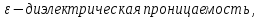

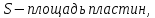
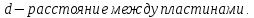
Электрическое поле сосредоточено внутри конденсатора. Энергия заряженного конденсатора вычисляется по формуле: .

Основное применение конденсаторов - в радиотехнике. Также они применяются в лампах-вспышках, в газоразрядных лампах.