Когда зарядов много, при расчётах полей возникают некоторые трудности.
Преодолеть их помогает теорема Гаусса. Суть теоремы Гаусса сводится к следующему: если произвольное количество зарядов мысленно окружить замкнутой поверхностью S, то поток напряжённости электрического поля через элементарную площадку dS можно записать как dФ = Есоsα۰dS где α - угол между нормалью к плоскости и вектором напряжённости 
. (рис.12.7)
Полный же поток через всю поверхность будет равен сумме потоков от всех зарядов, произвольным образом распределённых внутри её и пропорционально величине этого заряда
(12.9)
Определим поток вектора напряжённости сквозь сферическую поверхность радиуса r, в центре которой расположен точечный заряд +q (рис.12.8). Линии напряжённости перпендикулярны поверхности сферы, α =0, следовательно соsα = 1. Тогда
или 
Если поле образовано системой зарядов, то
Теорема Гаусса: поток вектора напряжённости электростатического поля в вакууме сквозь любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, делённой на электрическую постоянную.
(12.10)
Если внутри сферы зарядов нет, то Ф = 0.
Теорема Гаусса позволяет сравнительно просто рассчитать электрические поля при симметрично распределённых зарядов.
Введём понятие о плотности распределенных зарядов.
· Линейная плотность обозначается τ и характеризует заряд q, приходящийся на единицу длины ℓ. В общем виде может быть рассчитана по формуле
(12.11)
При равномерном распределении зарядов линейная плотность равна 
· Поверхностная плотность обозначается σ и характеризует заряд q, приходящийся на единицу площади S. В общем виде определяется по формуле
(12.12)
При равномерном распределении зарядов по поверхности поверхностная плотность равна 
· Объёмная плотность обозначается ρ, характеризует заряд q, приходящийся на единицу объёма V. В общем виде определяется по формуле
(12.13)
При равномерном распределении зарядов она равна 
.
o Н 
апряжённость электростатического поля равномерно заряженной сферы (рис.12.9), имеющей радиус r0. Найдём модуль вектора в какой-либо точке А, находящейся на расстоянии r1 от центра этой сферы.
Так как заряд q располагается на сфере равномерно, то
σ = const. Применим теорему Гаусса. Проведём сферу радиусом через точку А. Поток вектора напряжённости рис.12.9 сквозь сферическую поверхность радиуса равен 
соsα = 1, так как α = 0. По теореме Гаусса, 
.
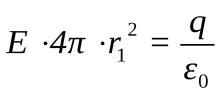или 
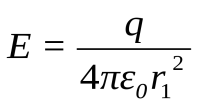(12.14)
Из выражения (12.14) следует, что напряжённость поля вне заряженной сферы такая же, как напряжённость поля точечного заряда, помещённого в центре сферы. На поверхности сферы, т.е. r1 = r0, напряжённость 
.
Внутри сферы r1 < r0 (рис.12.9) напряжённость Е = 0, так как сфера радиусом r2 внутри никаких зарядов не содержит и, по теореме Гаусса, поток вектора сквозь такую сферу равен нулю.
o Н 
апряжённость поля, создаваемого равномерно заряженным бесконечно длинным цилиндром
Цилиндр радиусом r0 равномерно заряжен с поверхностной плотностью σ (рис.12.10). Определим напряжённость поля в произвольно выбранной точке А. Проведём через точку А воображаемую цилиндрическую поверхность радиусом R и длиной ℓ. Вследствие симметрии поток будет выходить только через боковые поверхности цилиндра, так как заряды на цилиндре радиуса r0 распределены по его поверхности равномерно, т.е. линии напряжённости будут радиальными прямыми, перпендикулярными боковым поверхностям обоих цилиндров. Так как поток через основание цилиндров равен нулю (cos α = 0), а боковая поверхность цилиндра перпендикулярна силовым линиям (cos α = 1), то
или
(12.15)
Выразим величину Е через σ - поверхностную плотность. По определению,
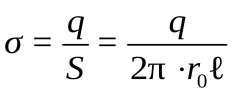следовательно, 
Подставим значение q в формулу (12.15)
(12.16)
По определению линейной плотности,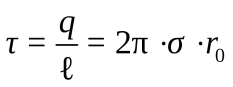 
, откуда 
; подставляем это выражение в формулу (12.16):
(12.17)
т.е. напряжённость поля, создаваемого бесконечно длинным заряженным цилиндром, пропорциональна линейной плотности заряда и обратно пропорциональна расстоянию.
o Напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью
Определим напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью в точке А. Пусть поверхностная плотность заряда плоскости равна σ. В качестве замкнутой поверхности удобно выбрать цилиндр, ось которого перпендикулярна плоскости, а правое основание содержит точку А. Плоскость делит цилиндр пополам. Очевидно, что силовые линии перпендикулярны плоскости и параллельны боковой поверхности цилиндра, поэтому весь поток проходит только через основания цилиндра. На обоих основаниях напряжённость поля одинакова, т.к. точки А и В симметричны относительно плоскости. Тогда поток, через основания цилиндра равен
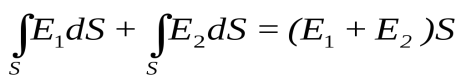
Согласно теореме Гаусса,
Так как 
, то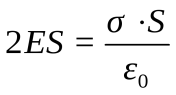 
, откуда
(12.18)
Таким образом, напряжённость поля бесконечной заряженной плоскости пропорциональна поверхностной плотности заряда и не зависит от расстояния до плоскости. Следовательно, поле плоскости является однородным.
o Напряжённость поля, создаваемого двумя разноименно равномерно заряженными параллельными плоскостями
Результирующее поле, создаваемое двумя плоскостями, определяется по принципу суперпозиции полей: 
(рис.12.12). Поле, создаваемое каждой плоскостью, является однородным, напряжённости этих полей равны по модулю, но противоположны по направлению: 
. По принципу суперпозиции напряжённость суммарного поля вне плоскости равна нулю:
Между плоскостями напряжённости полей имеют одинаковые направления, поэтому результирующая напряжённость равна
(12.19)
Таким образом, поле между двумя разноименно равномерно заряженными плоскостями однородно и его напряжённость в два раза больше, чем напряжённость поля, создаваемого одной плоскостью. Слева и справа от плоскостей поле отсутствует. Такой же вид имеет и поле конечных плоскостей, искажение появляется только вблизи их границ. С помощью полученной формулы можно рассчитать поле между обкладками плоского конденсатора.
Работа электростатического поля по перемещению заряда. Потенциал электростатического поля. Потенциал поля точечного заряда, заряженной сферы. Разность потенциалов.
На заряд qпр помещённый в произвольную точку электростатического поля с напряжённостью Е, действует сила F= qпр E. Если заряд не закреплён, то сила заставит его перемещаться и, значит, будет совершаться работа. Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда qпр из точки а электрического поля в точку b на отрезке пути dℓ, по определению, равна
dA = Fdℓcosα
(
α - угол между F и направлением движения) (рис.12.13).
Если работа совершается внешними силами, то dA< 0, если силами поля, то dA > 0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении qпр из точки a в точку b
(12.20)
Рисунок -12.13
(
- кулоновская сила, действующая на пробный зарядqпр в каждой точке поля с напряжённостью E).
Тогда работа
(12.21)
Перемещение совершается перпендикулярно вектору 
, следовательноcosα =1, работа переноса пробного заряда qпр от a к b равна
(12.22)
Работа сил электрического поля при перемещении заряда не зависит от формы пути, а зависит лишь от взаимного расположения начальной и конечной точек траектории.
Следовательно, электростатического поля точечного заряда является потенциальным, а электростатические силы – консервативными.
Это свойство потенциальных полей. Из него следует, что работа совершаемая в электрическом поле по замкнутому контуру, равна нулю:
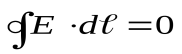(12.23)
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: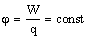 
- энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
| 
|
| Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. | |
- следствие принципа суперпозиции полей (потенциалы складываются алгебраически).
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.
В СИ потенциал измеряется в вольтах: 
| |
| Разность потенциалов | |
| |
| Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! | 
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
| 
|
4. Потенциал поля объемно заряженного шара 
.
Для простоты расчетов примем 
.
Зависимость 
для этого случая представлена на рисунке. Потенциал точек внутри шара 
равен заштрихованной площади, согласно геометрическому смыслу интеграла:
,
т 
ак как потенциал равен работе по перемещению единичного положительного из данной точки в бесконечность, где потенциал принят равным нулю.
Учитывая зависимость:
где 
, получаем для точек внутри шара:
.
Д 
ля точек вне шара 
потенциал убывает с расстоянием как поле точечного заряда:
.
Зависимость 
представлена на рисунке, где
,
.
Связь напряженности и потенциала электростатического поля. Эквипотенциальные поверхности и линии напряженности. Разность потенциалов между точками поля объемно заряженного шара, между двумя точками поля равномерно заряженной бесконечно протяженной плоскости и между двумя равномерно заряженными плоскостями.
Связь между этими величинами аналогична связи между потенциальной энергией и консервативной силой:
(3.1)
где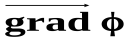 
– градиент потенциала, ВФВ, равная возрастанию потенциала в определенном направлении. Знак минус показывает, что вектор напряжённости поля направлен в сторону убывания потенциала (рис. 29).
Эта формула выражает фундаментальную связь между напряженностью и потенциалом: напряжённость поля равна градиенту потенциала со знаком минус.
Если перемещение происходит только вдоль направления оси ОХ, то можно записать:
.
Связь между напряжённостью и потенциалом позволяет по известной напряжённости поля найти разность потенциалов между двумя произвольными точками:
.
Электростатическое поле можно охарактеризовать совокупностью силовых и эквипотенциальных линий.
Силовая линия – это мысленно проведенная в поле линия, начинающаяся на положительно заряженном теле и заканчивающаяся на отрицательно заряженном теле, проведенная таким образом, что касательная к ней в любой точке поля дает направление напряженности в этой точке.
Силовые линии замыкаются на положительных и отрицательных зарядах и не могут замыкаться сами на себя.
Под эквипотенциальной поверхностью понимают совокупность точек поля, имеющих один и тот же потенциал (
).
Если рассечь электростатическое поле секущей плоскостью, то в сечении будут видны следы пересечения плоскости с эквипотенциальными поверхностями. Эти следы называют эквипотенциальными линиями.
Эквипотенциальные линии являются замкнутыми сами на себя.
Силовые линии и эквипотенциальные линии пересекаются под прямым углом.
Р 
ассмотрим эквипотенциальную поверхность:
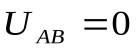(так как точки лежат на эквипотенциальной поверхности).
– скалярное произведение
Поле объемно заряженного шара радиуса R с общим зарядом Q вне шара (r>R) вычисляется по формуле (82.3), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r 1и r 2 от центра шара (r 1 >R, r 2 >R), определяется формулой (86.2). В любой точке, лежащей внутри шара на расстоянии r' от его центра (r'<R), напряженность определяется выражением (82.4): E =(1/4pe0)(Q/R3)r'.Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r '1и r '2 от центра шара (r' 1 <R, r' 2< R), равна
1. Поле равномерно заряженной бесконечной плоскости определяется формулой (82.1): E=s/(2e0), где s — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х 1, и x2от плоскости
(используем формулу (85.1)), равна
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой (82.2): Е=s/e 0, где s— поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно d (см. формулу (85.1)), равна
