С использованием теории графов могут быть решены следующие экономические задачи:
1) о соединении городов (задача о построении минимального остовного дерева);
2) о кратчайшем маршруте;
3) о пропускной способности сети дорог (задача о максимальном потоке);
4) о назначениях;
5) о выборе оптимальной стратегии поведения в условиях неопределенности.
Задача о соединении городов
Постановка задачи. Имеется 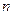 городов
городов  ,
,  , …,
, …,  , которые нужно соединить между собой сетью дорог. Стоимость строительства дороги
, которые нужно соединить между собой сетью дорог. Стоимость строительства дороги  известна и равна
известна и равна  . Какой должна быть сеть дорог, чтобы стоимость ее строительства была минимальной?
. Какой должна быть сеть дорог, чтобы стоимость ее строительства была минимальной?
Замечание. В качестве величин  также может выступать расстояние между городами, время, затрачиваемое на переезд и т.п. Величину
также может выступать расстояние между городами, время, затрачиваемое на переезд и т.п. Величину  называют длиной ребра.
называют длиной ребра.
В терминах теории графов задачу можно сформулировать следующим образом: используя 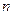 вершин
вершин  ,
,  , …,
, …,  , построить граф, имеющий минимальную суммарную длину ребер.
, построить граф, имеющий минимальную суммарную длину ребер.
Теорема 11. Граф, имеющий минимальную суммарную длину ребер, является минимальным остовным деревом.
Замечание. В силу определения, минимальное остовное дерево не имеет циклов. В противном случае (то есть граф имеет цикл) можно удалить одно ребро графа, стоимость сети уменьшится, а города останутся соединенными. Следовательно, по теореме 10, число ребер графа, имеющего 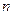 вершин, должно быть
вершин, должно быть  .
.
Алгоритм реализации
1) Составить список всех ребер графа в порядке возрастания их длины (стоимости).
2) Из списка всех ребер графа выбрать ребро с минимальной длиной и исключить его из списка всех ребер.
3) Из списка всех оставшихся ребер выбрать ребро, имеющее минимальную длину. При поиске добавляемого ребра надо перебирать все ребра, имеющие общую вершину с уже построенной сетью. Если при этом имеется несколько ребер одинаковой длины, то выбирают любое из них.
4) Проверить, чтобы выбранное ребро не образовывало цикла ни с одним из ранее выбранных ребер. Если цикл образуется, то исключить данное ребро из общего списка ребер и перейти к следующему ребру. Если цикл не образуется, то включить данное ребро в минимальное остовное дерево и исключить из общего списка ребер.
5) Пункты 3), 4) данного алгоритма повторять до тех пор, пока число ребер в списке, составляющем минимальное остовное дерево, станет равным  .
.
6) Стоимость построенной сети вычислить по формуле  .
.
Пример 36.9. Сетью дорог нужно соединить города А, В, D и F. Стоимость строительства дорог, соединяющих любые два города, известна и в условных денежных единицах приведена в таблице:
| города | А | В | D | F |
| А | – | |||
| В | – | |||
| D | – | |||
| F | – |
Найти самую дешевую сеть соединения городов и ее стоимость.
Решение. Надо соединить четыре города, следовательно, сеть дорог будет состоять из трех ребер.
1) Список ребер и их стоимостей представлен в условии в таблице.
2) Ребро минимальной длины  ,
,  .
.
3) Из оставшихся ребер минимальную длину имеет 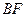 ,
,  .
.
4) При соединении ребер  и ВF цикл не образуется. Соединены города D, В, F. Так как в построенном минимальном остовном дереве только два ребра
и ВF цикл не образуется. Соединены города D, В, F. Так как в построенном минимальном остовном дереве только два ребра  и
и 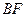 , то продолжим поиск.
, то продолжим поиск.
 5) Ребро минимальной длины из оставшихся ребер
5) Ребро минимальной длины из оставшихся ребер  (
( ) не подходит, так как
) не подходит, так как 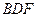 – цикл, а город А не соединен. Исключаем из общего списка ребро
– цикл, а город А не соединен. Исключаем из общего списка ребро  и выбираем ребро
и выбираем ребро 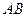 , которое имеет минимальную длину из оставшихся ребер (
, которое имеет минимальную длину из оставшихся ребер (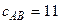 ) и не образует цикла с ребрами, включенными в минимальное остовное дерево.
) и не образует цикла с ребрами, включенными в минимальное остовное дерево.
Таким образом, искомая сеть дорог состоит из звеньев АВ, ВF и ВD (рис. 36.13), ее стоимость  ден. ед.
ден. ед.
Ответ. Сеть дорог состоит из звеньев АВ, ВF и ВD, ее стоимость  ден. ед.
ден. ед.