Задачи, послужившие основой теории графов
Задача о кенигсбергских мостах
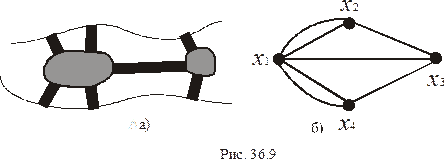
Постановка задачи (Л. Эйлер, 1736 г.). На рис. 36.9, а) схематически изображена карта города Кенигсберга, относящаяся к XVIII в. Город был расположен на берегах и двух островах реки Преголи (Прегель). Острова между собой и берегами были связаны семью мостами. Можно ли, выйдя из дома, вернуться обратно, пройдя по каждому мосту только один раз?
Так как при решении задачи интересны только переходы по мостам, то план города можно представить в виде полностью неориентированного мультиграфа (рис. 36.9, б)). Вершины  и
и 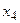 соответствуют правому и левому берегам реки, вершины
соответствуют правому и левому берегам реки, вершины  и
и 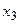 – островам; ребра мультиграфа – мостам. На языке графов задача формулируется следующим образом: существует ли в мультиграфе простой цикл, содержащий все ребра?
– островам; ребра мультиграфа – мостам. На языке графов задача формулируется следующим образом: существует ли в мультиграфе простой цикл, содержащий все ребра?
Определение 42. Простой цикл, содержащий все ребра графа, называют эйлеровым циклом (циклом Эйлера).
Замечание. Другими словами, эйлеров цикл проходит по каждому ребру ровно один раз.
Л. Эйлер сформулировал и доказал необходимое и достаточное условие того, чтобы в произвольном полностью неорентированном связном мультиграфе существовал эйлеров цикл.
Теорема 6. Эйлеров цикл в симметрическом связном мультиграфе существует тогда и только тогда, когда все его вершины являются четными.
Заметим, что в задаче о кенигсбергских мостах все вершины графа являются нечетными. Поэтому данная задача решения не имеет.
Определение 43. Граф, все вершины которого четны, называют эйлеровым графом.
Определение 44. Простой путь, содержащий все ребра графа, называют эйлеровым путем (путем Эйлера).
Теорема 7. У связного графа с двумя единственными нечетными вершинами существует эйлеров путь тогда и только тогда, когда этот путь начинается в одной из нечетных вершин и заканчивается в другой.
Задача о размещении экспозиции. Устроители больших художественных выставок часто вынуждены решать одну и ту же задачу: как организовать осмотр так, чтобы дать возможность в отведенное время ознакомиться с экспозицией наибольшему числу желающих. Для этого нужно расставить указатели таким образом, чтобы, перемещаясь в соответствии с предложенными в них рекомендациями, любой посетитель мог побывать у каждой картины ровно по одному разу. Возникает вопрос: можно ли найти общую методику организации осмотра выставки?
Если рассматривать стены и стенды, на которых размещены картины, как ребра, а точки поворотов как вершины, то помещение, в котором проводится выставка, будет представлять собой некоторый граф. Тогда задача об оптимальном размещении экспозиции сводится к построению на этом графе эйлерова цикла, если вход на экспозицию совпадает с выходом, и эйлерова пути, если вход и выход различны.
Алгоритм построения эйлерова цикла
1) Убедиться, что граф эйлеров.
2) Построить любой цикл. После построения возникают 2 возможности:
а) в цикл входят все ребра, и тогда задача решена;
б) на графе остались не пройденные ребра.
3) В построенном цикле найти вершину, из которой выходит еще не пройденное ребро (таких ребер должно быть четное число, если граф эйлеров).
4) Построить цикл из не пройденных ребер.
Алгоритм продолжать до тех пор, пока не будут пройдены все ребра.
Задача о коммивояжере
Постановка задачи (У.Р. Гамильтон). Район, который должен посетить бродячий торговец (коммивояжер), содержит некоторое количество городов, расстояния между которыми известны. Требуется найти маршрут, проходящий через все пункты по одному разу и возвращающийся в исходную точку. Если таких маршрутов несколько, то выбрать наиболее короткий из них.
Определение 45. Цепь, проходящую через каждую вершину полностью неориентированного графа 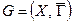 ровно по одному разу, называют гамильтоновой цепью.
ровно по одному разу, называют гамильтоновой цепью.
Определение 46. Цикл, проходящий через все вершины полностью неориентированного графа 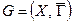 ровно одному разу через каждую (за исключением исходной, совпадающей с последней), называют гамильтоновым циклом.
ровно одному разу через каждую (за исключением исходной, совпадающей с последней), называют гамильтоновым циклом.
Определение 47. Путь, проходящий через все вершины графа 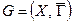 ровно по одному через каждую, называют гамильтоновым путем.
ровно по одному через каждую, называют гамильтоновым путем.
В терминах теории графов задача о коммивояжере равносильна задаче поиска на некотором полностью неориентированном графе элементарного гамильтонова цикла.
Задача поиска гамильтонова цикла является более сложной по сравнению с задачей поиска эйлерова цикла, так как, во-первых, пока не найдено достаточно общих теорем существования гамильтоновых циклов; во-вторых, пока не получено достаточно эффективных алгоритмов, позволяющих находить кратчайший путь, отличающихся по объему вычислений от простого перебора вариантов. Однако, доказано несколько утверждений, позволяющих определять наличие гамильтонова цикла у графа.
Теорема 8. Если степень каждой вершины графа 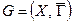 , имеющего
, имеющего 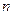 вершин, удовлетворяет соотношению
вершин, удовлетворяет соотношению 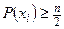 , то граф имеет гамильтонов цикл.
, то граф имеет гамильтонов цикл.
Теорема 9. Всякий полный граф является гамильтоновым.
К задаче о построении гамильтонова цикла сводится задача о выборе маршрута кругосветного путешествия или экскурсии по достопримечательностям города.