Постановка задачи. Задана сеть дорог, соединяющая несколько населенных пунктов, расстояния между которыми известны. Требуется найти наиболее короткий (оптимальный) маршрут из одного заданного города в другой.
Замечание. Вместо расстояний между населенными пунктами могут быть известны стоимости доставки единицы груза из пункта в пункт, время, затрачиваемое на переезд из пункта в пункт.
В терминах теории графов задачу можно сформулировать следующим образом: между двумя заданными вершинами графа найти цепь с минимальной длиной ребер.
Данная задача может быть решена методом динамического программирования (тема 35, п. 35.2) с минимизируемой целевой функцией, выражающей стоимость затрат на перевозку единицы груза из начального пункта в пункт назначения.
 Пример 36.10. Найти наиболее экономный маршрут перевозки груза из города
Пример 36.10. Найти наиболее экономный маршрут перевозки груза из города  в город
в город  и стоимость перевозки для сети дорог, показанной на рис. 36.14. Над ребрами сети указаны стоимости перевозки единицы груза из одного города в другой (в ден. ед.).
и стоимость перевозки для сети дорог, показанной на рис. 36.14. Над ребрами сети указаны стоимости перевозки единицы груза из одного города в другой (в ден. ед.).
Решение. Математическая модель задачи. Система S: транспорт с грузом, который нужно переместить из пункта  в пункт
в пункт  , и сеть дорог, соединяющая эти пункты.
, и сеть дорог, соединяющая эти пункты.
Представим процесс перевозки груза как многошаговый процесс. Для этого сгруппируем населенные пункты следующим образом. К группе  отнесем пункт
отнесем пункт  , к группе
, к группе  все пункты, в которые можно попасть из
все пункты, в которые можно попасть из  , то есть
, то есть  и
и  . К группе
. К группе  – все пункты, куда можно попасть из
– все пункты, куда можно попасть из  и
и  , то есть
, то есть 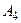 ,
,  ,
, 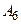 . В группу
. В группу  – все, куда можно попасть из
– все, куда можно попасть из 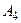 ,
,  ,
, 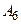 , то есть
, то есть  ,
,  ,
,  . К группе
. К группе  – пункт
– пункт  . Результат группировки удобно представить в виде таблицы:
. Результат группировки удобно представить в виде таблицы:

| 
| 
| 
| 
|

| 
| 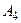
| 
| 
|

| 
| 
| ||
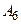
| 
|
Тогда движение транспорта с грузом из пункта  в пункт
в пункт  можно представить как
можно представить как  -шаговый процесс: на первом шаге груз перемещают из пункта группы
-шаговый процесс: на первом шаге груз перемещают из пункта группы  в пункт группы
в пункт группы  ; на втором шаге – из пункта группы
; на втором шаге – из пункта группы  в пункт группы
в пункт группы  ; на третьем шаге – из пункта группы
; на третьем шаге – из пункта группы  в пункт группы
в пункт группы  ; на четвертом шаге – из пункта группы
; на четвертом шаге – из пункта группы  в пункт группы
в пункт группы  . Таким образом, формирование наиболее экономного маршрута может быть реализовано за
. Таким образом, формирование наиболее экономного маршрута может быть реализовано за  шага.
шага.
Составленная таблица содержит сведения о множестве состояний  – множестве местонахождений транспорта с грузом в некотором пункте группы с номером
– множестве местонахождений транспорта с грузом в некотором пункте группы с номером  . Множество начальных состояний
. Множество начальных состояний  . Множество конечных состояний
. Множество конечных состояний  . Множество состояний в начале
. Множество состояний в начале  -го шага:
-го шага:  – множество пунктов группы с номером
– множество пунктов группы с номером 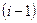 (откуда выезжает транспорт с грузом). Управление
(откуда выезжает транспорт с грузом). Управление  на
на  -м шаге: выбор дороги
-м шаге: выбор дороги  , по которой следует направить груз из данного населенного пункта в соседний в общем направлении к пункту
, по которой следует направить груз из данного населенного пункта в соседний в общем направлении к пункту  . Множество состояний в конце
. Множество состояний в конце  -го шага:
-го шага:  – множество пунктов группы с номером
– множество пунктов группы с номером  (куда прибывает транспорт с грузом в результате принятого управления). Целевая функция
(куда прибывает транспорт с грузом в результате принятого управления). Целевая функция  на
на  -м шаге – затраты на перевозку единицы груза из данного пункта в выбранный соседний пункт. Рекуррентные соотношения Р. Беллмана имеют вид
-м шаге – затраты на перевозку единицы груза из данного пункта в выбранный соседний пункт. Рекуррентные соотношения Р. Беллмана имеют вид

Воспользуемся алгоритмом метода динамического программирования.
Условная оптимизация
1) На четвертом шаге требуется найти условно оптимальные значения целевой функции при транспортировке груза из пунктов группы  в
в  . Тогда управление
. Тогда управление  – выбор дороги для доставки. Условно оптимальные значения целевой функции равны затратам при передвижении по этим дорогам. Целевая функция однозначна на каждом шаге. Вычисления проведем в виде таблицы:
– выбор дороги для доставки. Условно оптимальные значения целевой функции равны затратам при передвижении по этим дорогам. Целевая функция однозначна на каждом шаге. Вычисления проведем в виде таблицы:
Таблица 36.1
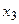
| 
| 
| 
|

| 
| 
| |

| 
| 
| |

| 
| 
|
2) На третьем шаге требуется найти условно оптимальные значения целевой функции при транспортировке груза из пунктов группы  в
в  , причем путь из пунктов группы
, причем путь из пунктов группы  в
в  уже оптимизирован и представлен в последнем столбце табл. 36.1. Вычисления проведем в виде таблицы:
уже оптимизирован и представлен в последнем столбце табл. 36.1. Вычисления проведем в виде таблицы:
Таблица 36.2
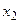
| 
| 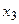
| 
| 
| 
| 
|
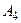
| 
| 
| ||||

| 
| |||||

| 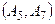
| 
| ||||

| 
| |||||
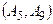
| 
| |||||
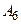
| 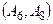
| 
|
3) На втором шаге требуется найти условно оптимальные значения целевой функции при транспортировке груза из пунктов группы  в
в  , причем путь из пунктов группы
, причем путь из пунктов группы  через пункты группы
через пункты группы  в
в  уже оптимизирован и представлен в последнем столбце табл. 36.2. Вычисления проведем в виде таблицы:
уже оптимизирован и представлен в последнем столбце табл. 36.2. Вычисления проведем в виде таблицы:
Таблица 36.3

| 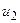
| 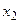
| 
| 
| 
| 
|

| 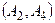
| 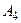
| ||||

| 
| |||||

| 
| 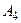
| ||||

| 
| |||||

| 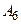
|
На первом шаге требуется найти условно оптимальные значения целевой функции при транспортировке груза из пункта  в пункт
в пункт 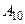 , причем путь из пунктов группы
, причем путь из пунктов группы  через пункты групп
через пункты групп  и
и  в
в 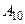 уже оптимизирован и представлен в последнем столбце табл. 36.3. Вычисления проведем в виде таблицы:
уже оптимизирован и представлен в последнем столбце табл. 36.3. Вычисления проведем в виде таблицы:
Таблица 36.4

| 
| 
| 
| 
| 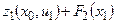
| 
|

| 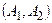
| 
| ||||

| 
|
Этап условной оптимизации завершен.
Безусловная оптимизация
Проанализируем результаты вычислений. Согласно табл. 36.4 получаем, что минимальная стоимость перевозки груза из пункта  в пункт
в пункт 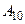 равна
равна  ден. ед. Этой стоимости соответствует дорога
ден. ед. Этой стоимости соответствует дорога  . В табл. 36.3, в строке
. В табл. 36.3, в строке  , находим минимальную стоимость перевозки на оставшемся пути
, находим минимальную стоимость перевозки на оставшемся пути  ден. ед., ей соответствует дорога
ден. ед., ей соответствует дорога  . В табл. 36.2, в строке
. В табл. 36.2, в строке 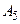 , минимальной стоимости оставшегося пути
, минимальной стоимости оставшегося пути  ден. ед. соответствует две дороги
ден. ед. соответствует две дороги 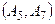 или
или  . В табл. 36.1 строке
. В табл. 36.1 строке  соответствует минимальная стоимость оставшегося пути
соответствует минимальная стоимость оставшегося пути  ден. ед. и дорога
ден. ед. и дорога  , а строке
, а строке  – минимальная стоимость
– минимальная стоимость 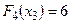 ден. ед. и дорога
ден. ед. и дорога  .
.
Ответ. Минимальная стоимость перевозки груза из пункта  в пункт
в пункт  14 ден. ед. Наиболее экономные маршруты:
14 ден. ед. Наиболее экономные маршруты:  и
и  .
.
Теоретический материал: [2, гл. 30], [10, гл. 4], [12, гл. 30], [22, гл. 4], [24, гл. 2], [26, гл. 3], [28].