Измерение бета-активности образца

Государственное образовательное учреждение

Высшего профессионального образования

Южно-Уральский государственный университет

Кафедра оптики и спектроскопии

Лаборатория микрофизики

ЛАБОРАТОРНАЯ РАБОТА № 6

ОПРЕДЕЛЕНИЕ ПЕРИОДА ПОЛУРАСПАДА ДОЛГОЖИВУЩЕГО ИЗОТОПА

Челябинск

Введение

Радиоактивностью называют явление самопроизвольного испускания ядрами элементарных частиц и ядер других элементов. Впервые самопроизвольный распад ядер был обнаружен французским физиком А. Беккерелем[1] в 1896 году. Ядро урана испускает альфа–частицу (ядро гелия-4) и превращается в ядро другого химического элемента. Этот процесс получил название альфа-распада. Позднее было открыто испускание ядрами электронов (бета-распад) и гамма-излучения. Количество распадов ядер, происходящих за единицу времени, называется активностью. Единицей активности в системе СИ является беккерель(Бк): 1Бк =1 распад в секунду. В атомной промышленности используется также внесистемная единица кюри [2] (Ки): 1Ки=3,7·10¹⁰ Бк. Единица кюри была первоначально введена как активность 1 грамма изотопа радия .

Как показали опыты, активность в радиоактивном образце, содержащий один изотоп, представляет собой экспоненциально убывающую функцию времени. Обозначим через 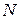число радиоактивных ядер в образце. Как показали Резерфорд[3] и Содди[4] число распадающихся ядер за малый промежуток времени пропорционально общему числу радиоактивных ядер:

,

(1)

где знак минус указывает на уменьшение числа радиоактивных ядер со временем. Величина называется постоянной распада. Ее смысл - вероятность распада отдельного ядра в единицу времени. Интегрируя (1) с учетом того, что , получим основной закон радиоактивного распада, хорошо согласующийся с экспериментальными результатами:

.

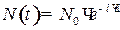(2)

Промежуток времени, в течение которого число радиоактивных ядер уменьшается вдвое, называется периодом полураспада . Легко убедиться, что период полураспада и постоянная распада связаны соотношением:

.

(3)

Активность образца определяется выражением . Принимая во внимание формулы (1) и (2), получим:

.

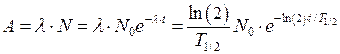(4)

Периоды полураспада•различных ядер изменяются в очень широких пределах; от долей.секунды до миллиардов лет. Изотоп тория имеет, например, период полураспада лет. Активность долгоживущих изотопов остается практически неизменной за любое реальное время наблюдения. При в уравнении (4) экспоненциальный множитель близок к единице и активность может быть представлена в виде:

.

(5)

Таким образом, определить экспериментально период полураспада короткоживущего изотопа можно по изменению во времени активности образца, используя (4), а для долгоживущих изотопов – по измерению активности и числа радиоактивных ядер в препарате.

В данной работе исследуется естественная радиоактивность долгоживущего изотопа калия , испытывающего бета-распад. Радиоактивное превращение ядра калия , может произойти двумя путями. Первый путь – ядро испускает электрон, называемый бета-частицей, и антинейтрино (88% случаев распада):

.

Второй путь - ядро захватит один из электронов атомной оболочки, испуская нейтрино (12% случаев):

.

Нейтрино 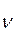и антинейтрино ввиду чрезвычайно малой интенсивности взаимодействия и веществом не могут быть зарегистрированы в используемой здесь экспериментальной установке. Бета-частицы, имеющие максимальную энергию 1,32 МэВ, и гамма-излучение, сопровождающее переход образующегося возбужденным ядра аргона в основное состояние, могут быть зарегистрированы в установке.

Таким образом, измеряя активность образца и количество радиоактивных ядер, можно из (5) найти период полураспада долгоживущего изотопа.

 

Методика эксперимента

2.1 Определение числа ядер изотопа ₁₉К⁴⁰ в образце

Известно, что в естественной смеси изотопов калия на долю приходятся 0,0119%. В данной работе используется соль и число радиоактивных атомов, содержащихся в образце массой 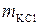, можно найти из закона Авогадро[5]:

.

(6)

где – число Авогадро, – масса киломоля .

Измерение бета-активности образца

Для определения бета-активности образца используется установка со счетчиком бега-частиц. Эффективность регистрации гамма-излучения, сопровождающего захват электрона, мала и можно считать, что счетчик регистрирует только бета-частяцы. На рисунке 1 приведена схема расположения радиоактивного образца и счетчика. Из рисунка видно, что только часть бета-частиц, испущенных образцом, попадет в рабочий объем счетчика. Поэтому для определения активности образца по измеренной скорости счета необходимо ввести ряд поправок, а именно, поправку на телесный угол, поправку на поглощение бета-частиц в объеме образца (самопоглощение), в воздушном промежутке и окошке счетчика, поправка на «мертвое время» счетчика и фон.

Рис.1 Схема расположения счетчика -частиц 1 и радиоактивного препарата 2 (соль ) в кювете 3.

2.2.1. Поправка на телесный угол определяется как отношение числа частиц, испускаемых в направлении рабочего объема счетчика, к полному числу частиц 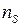, испускаемых препаратом в единицу времени во всех направлениях:

.

(7)

Данная поправка рассчитывается из геометрических соображений и приведена в таблице приложения. Для нахождения поправки нужно найти отношения и , где - длина стороны кюветы с солью, 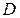- диаметр входного окошка счетчика, - расстояние от окошка счетчика до препарата (см. рис.1).

2.2.2. Поправка на самопоглощение и рассеяние бета-излучения в толстом образце определяется отношением числа частиц, вышедших из активного слоя, к полному числу частиц, образующихся в источнике. Приближенную оценку можно записать в виде:

,

(8)

где - коэффициент поглощения материала источника (г/см²), - массовая плотность образца (г/см³), - высота источника (см). Коэффициент поглощения материала источника может быть найден из эмпирической формулы:

,

(9)

где - максимальная энергия бета частицы задается в МэВ.

2.2.3. Поправка на поглощение бета-частиц в воздухе и входном окне счетчика представляет собой отношение числа частиц, вылетевших в направлении рабочего объема счетчика , к числу достигших его :

.

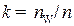(10)

Приближенно можно записать:

,

(11)

где – массовая толщина слоя поглощения между препаратом и счетчиком в (г/см²), , – массовые плотности в воздуха и входного окошка счетчика соответственно, – толщина входного окна.

2.2.4. «Мертвым временем» счетчика называется промежуток времени, прошедший с момента срабатывания счетчика после попадания в него частицы, в течение которого рабочий объем счетчика остается нечувствительности к регистрации. Обычно «мертвое время» газоразрядных счетчиков составляет около 10^-4с. Поправка на «мертвое время» необходима, чтобы учесть просчеты, связанные кратковременной потерей чувствительности детектора при регистрации частицы.

Пусть мертвое время равно , скорость счета импульсов в секунду при попадании в рабочий объем счетчика частиц в секунду. Значение по измеренной скорости и мертвому времени можно найти из выражения:

.

(12)

2.2.5. Фоном счетчика называются отсчеты в отсутствие исследуемого излучения. Причинами появления таких отсчетов являются естественная радиоактивность среды (как правило гамма-излучение почвы, стен здания и т.п.), космическое излучение, несовершество самого счетчика и др. В нашем случае это и регистрация счетчиком гамма-излучения радиоактивного препарата, обусловленное превращением в аргон посредством захвата атомного электрона. Поскольку проникающая способность всех излучений кроме измеряемого бета-излучения велика, для определения суммарного фона проводится измерение скорости счета при наличии между радиоактивным препаратом и счетчиком пластины из оргстекла толщиной не менее 0,5 см, задерживающей все бета-частицы. Число бета-частиц определяется как разность числа отсчетов в отсутствие и при наличия фильтра . Для учета всех распадов ядер , включая превращение его в аргон, необходимо разность умножить на коэффициент 1.136.

2.2.6. Порядок расчета активности по измеренной скорости счета n от радиоактивного препарата следует принять следующий: ввести поправку на разрешающее время и получить n₀, вычесть фон, учесть телесный угол, поглощение бета-частиц с помощью формул (8)-(11). В результате выражение для активности исследуемого образца будет иметь вид:

,

(13)

Можно исключить измерение высоты источника , если, известна масса соли 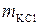и площадь образца :

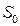2.2.7. Погрешность определения периода полураспада обусловлена случайным характером распада, приближениями, сделанными при выводе ряда расчетных формул и погрешностями прямых измерений длин, расстояний,.веса и т.п. Поскольку распад ядра является случайным процессом, то оказывается и число распадов ядер за фиксированное время. Известен закон распределения числа случайных событий - закон Пуассона (см. работу № 7). Если средне число зарегистрированных отсчетов , то среднеквадратичная ошибка равна .

Величина поправки, полученная по формуле (11) может отличаться от действительного значения до 20%. С такой же точностью известно значение мертвого времени счетчика. Погрешность значений коэффициента поглощения m равна 5%. Погрешность остальных величин, определяемых при нахождении периода полураспада, зависит от используемых инструментов и приборов. Погрешность окончательного результата находится как погрешность косвенного измерения.