Операции над высказываниями

Элементы математической логики

Высказывания и операции над ними

Понятие высказывания

Основным объектом математической логики является высказывание. Высказыванием называется повествовательное предложение, про которое можно сказать истинно оно или ложно, но не то и другое вместе. Высказывание обозначают большими латинскими буквами: А, В, С…

Не являются высказываниями предложения, содержащие определения (геометрической фигурой называется множество точек плоскости), призывы (храните деньги в сберегательной кассе!), вопросы (который час?).

Содержание высказывания не существенно: лишь бы это предложение могло быть либо истинным, либо ложным. Если высказывание истинно, будем говорить, что его значение истинности – истина; если ложно, то значение истинности – ложь.

Примеры решения задач

Являются ли предложения высказываниями?

А: «Сегодня идет снег»;

В: «5>3»;

С: «3 делится на 8»;

D: « +1 – простое число»;

Е: «Который час?»;

F: «Число 13 - несчастливое»;

G: «Существуют внеземные цивилизации»;

Решение. А: высказывание, может быть либо истинно, либо ложно;

В: всегда истинное высказывание;

С: всегда ложное высказывание;

D: высказывание, либо истинно, либо ложно, проверить нет возможности;

Е: не высказывание, т.к. предложение не является повествовательным;

F: не высказывание, так как судить о его истинности или ложности невозможно;

G: высказывание, хотя в настоящее время неизвестно истинно оно или ложно.

Задачи для самостоятельного решения

1) Какие из следующих предложений являются высказываниями? Какие из высказываний истинные, а какие — ложные?

1) Москва — столица СССР.

2) Студент физико-математического факультета педагогического института.

3) Треугольник ABC подобен треугольнику А'В'С'.

4) Луна есть спутник Марса.

5) .

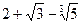6) Кислород — газ.

7) Каша — вкусное блюдо.

8) Математика — интересный предмет.

9) Картины Пикассо слишком абстрактны.

10) Железо тяжелее свинца.

11) Да здравствуют музы!

12) Треугольник называется равносторонним, если все его стороны равны.

13) Если в треугольнике все углы равны, то он равносторонний.

14) Сегодня плохая погода.

15) В романе А. С. Пушкина «Евгений Онегин» 136 245 букв.

16) Река Ангара впадает в озеро Байкал.

2) Какие из следующих высказываний истинны, а какие ложны?

a. «Сумма внутренних углов любого треугольника равна 180°.»;

b. «У всех кошек есть хвост.»;

c. «Найдется целое число х, удовлетворяющее соотношению х²=2. »;

d. «Существует простое четное число».

 

Операции над высказываниями

Для того, чтобы из высказываний получать новые высказывания применяются специальные операции – логические связки. Рассмотрим пять основных логических связок.

Отрицание высказывания А– это высказывание, которое истинно, если А ложно, и ложно, если А истинно. Обозначают или ùА.

Составим истинностную таблицу для операции отрицания:

А
И	Л
Л	И

Конъюнкцией высказываний А и В называется высказывание, которое истинно, если истинны А и В, и ложно во всех остальных случаях. Конъюнкцию обозначают АÙВ или А&В и называют логическим умножением. Таблица истинности выглядит следующим образом:

А	В	АÙВ
Л	Л	Л
Л	И	Л
И	Л	Л
И	И	И

Дизъюнкцией высказываний А и В называют высказывание, которое ложно, когда ложны оба высказывания А и В, а во всех других случаях истинно. Дизъюнкцию обозначают АÚВ и называют логическим сложением. Соответствующая этому высказыванию таблица истинности выглядит следующим образом:

А	В	АÚВ
Л	Л	Л
Л	И	И
И	Л	И
И	И	И

Импликацией высказываний А и В называют высказывание, которое ложно, когда А истинно, а В ложно, и истинно во всех остальных случаях. То есть из истины не может следовать ложь. Импликацию обозначают А®В или АÞВ и читают «из А следует В» или «если А, то В».

А	В	А®В
Л	Л	И
Л	И	И
И	Л	Л
И	И	И

Эквиваленцией высказываний А и В называется высказывание, которое истинно лишь в тех случаях, когда А и В имеют одинаковые истинностные значения. Эквиваленцию обозначают А«В или АÛВ и читают «А тогда и только тогда, когда В» или «Для того, чтобы А необходимо и достаточно, чтобы В».

А	В	А«В
Л	Л	И
Л	И	Л
И	Л	Л
И	И	И

Примеры решения задач

Рассмотрим предложение: «Если 2×2=5, то 7делится на 8». Определите его истинность.

Решение. Обозначим высказывание «2×2=5» буквой А, а высказывание «7делится на 8» буквой В. Тогда исходное предложение С=А®В. А – ложно, В – ложно, а С – истинно.

Составное высказывание V: «Если в треугольнике медиана не является высотой и биссектрисой, то этот треугольник не равнобедренный и не равносторонний.»запишите символически, введя буквенные обозначения для простых их составляющих:

Решение. Выделим и следующим образом обозначим простейшие составляющие высказывания:

А: «В треугольнике медиана является высотой»;

В: «В треугольнике медиана является биссектрисой»;

С: «Этот треугольник равнобедренный»;

D: «Этот треугольник равносторонний».

Тогда данное высказывание символически записывается так: 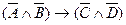.