Задачи для самостоятельного решения. Законы логики

1) Покажите, что высказывание логически эквивалентно утверждению .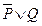

2) Докажите следующие равносильности.

а).

b). PÚ(QÙR) º(PÚQ)Ù(PÚR);

c).

d). P«QºP®QÙQ®P;

e).

3) Применяя равносильные преобразования, приведите следующие формулы к возможно более простой форме:

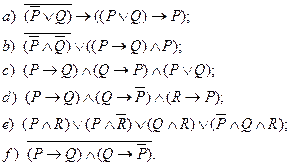
4) Следующие формулы преобразуйте равносильным образом так, чтобы они содержали только операции отрицания и конъюнкции:

5) Следующие формулы преобразуйте равносильным образом так, чтобы они содержали только операции отрицания и дизъюнкции:

6) Следующие формулы преобразуйте равносильным образом так, чтобы отрицание было отнесено только к пропозициональным переменным и не стояло бы перед скобками:

7) Следующие формулы преобразуйте равносильным образом так, чтобы они содержали только операции Ù, Ú, ù:

Законы логики

Формула логики называется законом логики, если она принимает значение «истина» при любых истинностных значениях входящих в нее высказывательных переменных.

Законы логики называются общезначимыми формулами или тавтологиями.

Формула называется тождественноложной или противоречием, если ее отрицание тождественно истинная формула.

Примеры решения задач

1) Дана формула: A=(p®q)®( ® ). Убедиться, что она является тавтологией.

Решение.

p	q	p®q			®	A
Л	Л	И	И	И	И	И
Л	И	И	И	Л	И	И
И	Л	Л	Л	И	Л	И
И	И	И	Л	Л	И	И

Так как для любых наборов переменных значение формулы «истина», то формула является законом логики или тавтологией.

2) С помощью равносильных преобразований докажите, что следующая формула является тождественно ложной (противоречием):

Решение: а) Покажем, что эта формула равносильна 0 (ложному высказыванию):

Задачи для самостоятельного решения

1) С помощью равносильных преобразований докажите, что следующие формулы являются тождественно ложными (противоречиями):

2) Составив таблицы истинности, докажите, что следующие формулы являются тавтологиями:

Правило логического вывода

Задача математической логики – дать принцип рассуждения, т.е. теорию вывода, критерии для решения механическим путем вопроса о том, можно ли некоторую цепочку рассуждений считать правильной. При этом важна только форма высказываний, составляющих цепочку, а не их содержание и смысл.

Высказывание В называется логическим следствием высказываний А₁, А₂, …, А_m, если В истинно всякий раз, когда каждое А_i, i=1, 2, … m, истинно. Это записывается так:

А₁, А₂, …, А_m╞B.

Высказывания А₁, А₂, …, А_m называются посылками логического следствия, а высказывание В – заключением.

Большинство теорем в математике имеют именно такую структуру. Доказать теорему – значит доказать, что заключение действительно является логическим следствием посылок. Самый простой способ – составить совместную таблицу истинности посылок и заключения, Найдите в ней строки, в которых все посылки имеют значение «истина», и убедиться, что заключение в этих строках также имеет значение «истина».

Примеры решения задач

1) Покажите, что A, C, AÙB® ╞ .

Решение. Для доказательства построим таблицу истинности:

А	В	С	AÙB®
Л	Л	Л	И	И
Л	Л	И	И	И
Л	И	Л	И	Л
Л	И	И	И	Л
И	Л	Л	И	И
И	Л	И	И	И
И	И	Л	И	Л
И	И	И	Л	Л

В таблице есть только одна строка (выделена), в которой все посылки принимают значение «истина». Видно, что заключение при этом также истинно. Таким образом, логическое следствие доказано.

2) Решите логическую задачу.

Один из трех братьев Витя, Толя, Коля разбил окно. В разговоре участвуют еще двое братьев — Андрей и Дима.

—Это мог сделать только или Витя, или Толя, — сказал Андрей.

— Я окно не разбивал, — возразил Витя, — и Коля тоже.

— Вы оба говорите неправду, — заявил Толя.

— Нет, Толя, один из них сказал правду, а другой сказал неправду, — возразил Дима.

— Ты, Дима, неправ, — вмешался Коля.

Их отец, которому, конечно, можно доверять, уверен, что трое братьев сказали правду. Кто разбил окно?

Решение. Введем обозначения для высказываний:

В: «Витя разбил окно»;.

Т: «Толя разбил окно»;

К: «Коля разбил окно».

Тогда высказывания братьев можно записать в символической форме следующим образом:

Образуем из высказываний А, V, L, D, М всевозможные конъюнкции по три высказывания: Поскольку из высказываний А, V, L, D, М только три истинны, то из десяти конъюнкций истинна лишь одна. Проверьте самостоятельно, что конъюнкции 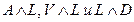ложны, а поэтому восемь из перечисленных конъюнкций ложны. Остаются две конъюнкции . Рассмотрим их:

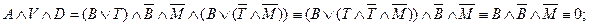
Итак, заключаем, что истинно высказывание , т. е. истинны высказывания T, . Следовательно, окно разбил Толя.