Во многих случаях закон распределения изучаемой случайно величины неизвестен, но есть основания предположить, что он имеет вполне определенный вид: нормальный, биномиальный или какой-либо другой.
Пусть необходимо проверить гипотезу Hq о том, что с. в. X подчиняется определенному закону распределения, заданному функцией распределения Fq(x), т. е. Hq: Fx{x) — Fq(х). Под альтернативной гипотезой Hi будем понимать в данном случае то, что просто не выполнена основная (т.е. Н\: Fx{%) ф Fq(x)).
Для проверки гипотезы о распределении случайной величины X проведем выборку, которую оформим в виде статистического ряда:
| Xi | XI | XI | Хщ | |
| щ | п 1 | П2 | Т1т |
т
где ^ щ = п — объем выборки.
г=1
Требуется сделать заключение: согласуются ли результаты наблюдений с высказанным предположением. Для этого используем специально подобранную величину — критерий согласия.
Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. (Он используется для проверки согласия предполагаемого вида распределения с опытными данными на основании выборки.)
Существуют различные критерии согласия: Пирсона, Колмогорова, Фишера, Смирнова и др.
Критерий согласия Пирсона — наиболее часто употребляемый критерий для проверки простой гипотезы о законе распределения.
Критерий х2 Пирсона
Для проверки гипотезы Но поступают следующим образом.
| (7.12) |
Разбивают всю область значений с. в. X на т интервалов Ai, Д2,...,Дт и подсчитывают вероятности pi (г — 1,2,...,т) попадания с. в. X (т.е. наблюдения) в интервал Д^, используя формулу Р{а ^ X ^ р} = Fo{/3) — Fo(at). Тогда теоретическое число значений с. в. X, попавших в интервал Д*, можно рассчитать по формуле п ■ р{. Таким образом, имеем статистический ряд распределения с. в. X (7.11) и теоретический ряд распределения:
| Ai | д2 | Am | |
| Tb[ = npi | п'2 = пр2 | пт = пРт |
Если эмпирические частоты (щ) сильно отличаются от теоретических (npi = nj), то проверяемую гипотезу Hq следует отвергнуть; в противном случае — принять.
| (7.11) |
Каким критерием, характеризующим степень расхождения между эмпирическими и теоретическими частотами, следует воспользоваться? В качестве меры расхождения между щ и npi для i = 1,2,..., т
К. Пирсон (1857-1936; англ. математик, статик, биолог, философ) предложил величину («критерий Пирсона»):
m, ч о т 2
2 ^ [Щ - ПРгУ ^ Щ
* =1. — Wi — = 1.т-п' (7ЛЗ)
t=l
Согласно теореме Пирсона, при п —> оо статистика (7.13) имеет х2_ распределение ск — т — г — 1 степенями свободы, где т — число групп (интервалов) выборки, г — число параметров предполагаемого распределения. В частности, если предполагаемое распределение нормально, то оценивают два параметра (аист), поэтому число степеней свободы к = т — 3.
Правило применения критерия х2 сводится к следующему:
1. По формуле (7.13) вычисляют х2абл — выборочное значение статистики критерия.
2. Выбрав уровень значимости а критерия, по таблице х2_распределения находим критическую точку (квантиль) Ха,к*
3. Если Хнабл ^ Xa,fc' то гипотеза Щ не противоречит опытным данным; если Хнабл ^ X2*> то гипотеза отвергается. Необходимым условием применения критерия Пирсона является
наличие в каждом из интервалов не менее 5 наблюдений (т. е. щ ^ 5). Если в отдельных интервалах их меньше, то число интервалов надо уменьшить путем объединения (укрупнения) соседних интервалов.
Пример 7.8. Измерены 100 обработанных деталей; отклонения от заданного размера приведены в таблице:
| [Яч, ^i+l) | [-3,-2) | [-2,-1) | [-1,0) | [0,1) | [1,2) | [2,3) | [3,4) | К,5) |
| Щ |
Проверить при уровне значимости а. — 0,01 гипотезу Но о том, что отклонения от проектного размера подчиняются нормальному закону распределения.
О Число наблюдений в крайних интервалах меньше 5, поэтому объединим их с соседними. Получим следующий ряд распределения (п - = 100):
| [-3,-1) | [-1,0) | [0,1) | [1,2) | [2,3) | [3,5) | |
| щ |
Случайную величину — отклонение — обозначим через X. Для вычисления вероятностей pi необходимо вычислить параметры, определяющие нормальный закон распределения (а и а). Их оценки вычислим
по выборке: х = щ • (-2 • 13 + (-0,5) • 15 +... + 4 • 10) = 0,885 «0,9, DB = 13 + 0,25-15 +... +16-10)-(0,885)2 и 2,809, сг «1,676 и 1,7.
Находим рг (i = 1,6). Так как с. в. X ~ N{a,o) определена на (—оо, оо), то крайние интервалы в ряде распределения заменяем, соответственно, на (—оо, —1) и (3, +оо). Тогда р\ = р{—оо < X < —1} =
~11~7° 9) фо(~°о) = ± - Ф0(1,12) = 0,1314. Аналогично получаем: р2 = 0,1667, рз = 0,2258, р4 = 0,2183, р5 = 0,1503, рб = = р{3 ^ X < оо} = Ф0(оо) - Ф0 = - Ф0(1,24) - 0,1075.
| 6 2 П7 |
| Хна&л ^ у |
| npi |
| t=l |
| Критерий Колмогорова Критерий Колмогорова для простой гипотезы является наиболее простым критерием проверки гипотезы о виде закона распределения. Он связывает эмпирическую функцию распределения F^(x) с функцией распределения F(x) непрерывной случайной величины X. |
Полученные результаты приведем в следующей таблице:
| [Xi,Xi+1) | (-оо,-1) | [-1,0) | [0,1) | [1,2) | [2,3) | [3, оо) |
| щ | ||||||
| п' = прг | 13,14 | 16,67 | 22,58 | 21,83 | 15,03 | 10,75 |
Вычисляем Хнабл: п =
= (щ4 + I& + " • + iS) ~ 100 ^ 101'045 " 1Щ
т е- *набл ~ !'045-
Находим число степеней свободы; по выборке рассчитаны два параметра, значит, г = 2. Количество интервалов 6, т. е. т — 6. Следовательно, А;~б — 2 — X = 3. Зная, что а — 0,01 и к = 3, по таблице х2-распределения находим xi,k = 11»3- Итак> Хнабл < следова

|
тельно, нет оснований отвергнуть проверяемую гипотезу. •
Пусть xi,x2i...,хп — конкретная выборка из распределения с неизвестной непрерывной функцией распределения F(rc) и F* (х) — эмпирическая функция распределения. Выдвигается простая гипотеза Но: F(x) = F0(;r) (альтернативная Ну. F(x) Ф Fq(x), х е К).
Сущность критерия Колмогорова состоит в том, что вводят в рассмотрение функцию
Dn = max \FZ(x) - F0(x)\, (7.14)
—oo<a:<oo
называемой статистикой Колмогорова, представляющей собой максимальное отклонение эмпирической функции распределения F*(x) от гипотетической (т. е. соответствующей теоретической) функции распределения Fo(x).
Колмогоров доказал, что при п оо закон распределения случайной величины у/п • Dn независимо от вида распределения с. в. X стремится к закону распределения Колмогорова'.
P{y/n-Dn < х} К(х),
где К(х) — функция распределения Колмогорова, для которой составлена таблица, ее можно использовать для расчетов уже при n ^ 20:
| а | од | 0,05 | 0,02 | 0,01 | 0,001 |
| Хо | 1,224 | 1,358 | 1,520 | 1,627 | 1,950 |
Найдем Do такое, что P{Dn > Z?o) = а.
Рассмотрим уравнение К{х) — 1 —а. С помощью функции Колмогорова найдем корень а?о этого уравнения. Тогда по теореме Колмогорова, Р{у/п • Dn < хо} = 1 - а, Р{у/п • Dn > жо} = а, откуда Д> =
у/п
Если Dn < Do, то гипотезу Hq нет оснований отвергать; в противном случае — ее отвергают.
Пример 7.9. Монету бросали 4040 раз (Бюффон). Получили щ = 2048 выпадений герба и п2 = 1992 выпадений решки. Проверить, используя а) критерий Колмогорова; б) критерий Пирсона, согласуются ли эти данные с гипотезой Но о симметричности монеты (а — 0,05).
О Случайная величина X принимает два значения: х\ = — 1 (решка) и х2 = 1 (герб). Гипотеза Но: Р{х — —1} = Р{х = 1} =
а) По таблице распределения Колмогорова находим корень урав-
Хо
нения К(х) = 1 — а при а ~ 0,05. Следует — 1,358. Тогда Do = -— =
у/п
= ^L » 0,021.
у/Шо
Для нахождения по выборке Dn строим функции Fq(x) и F*(x) и вычисляем величину Dn — max |F*(a;) ~ jPq(^)|.
| решка x\ ----- —1 | герб X2 — 1 | |
| Pi | 0,5 | 0,5 |
| Xi | решка X\ = —1 | герб x2 — 1 |
| Щ | ||
| pi | ~ 0,493 | ~ 0,507 |
0, при х ^ — 1, Fo(x) = ^ 0,5, при - 1 < х < 1,
1, при 1 < х.
0, при х ^ —1, •FnfaO = \ 0)493, при - 1 < х ^ 1,
1, при 1 < X.
Максимальное отклонение Fq (re) от F* (х) равно 0,007, т. е. Dn = = 0,007. Поскольку Dn < Z>o, то нет оснований отвергать гипотезу Hq\ опытные данные согласуются с гипотезой Hq о симметричности монеты.
б) Вычисляем статистику х2;
| 2048' |
| Хнабл ^ ^ |
| - 4040 - 0,776. |
| + |
| | •4040 |
2 п = 19922 .=1 ± ■ 4040
По таблице х^_ РаспРеДеления находим критическую точку Ха,к ~
= X0,05;i — 3,8. Так как Хнабл < Хо,05;1> то опытные данные согласуются с гипотезой о симметричности монеты. •
Упражнения
1. Распределение признака X (случайной величины X) в выборке задано следующей таблицей:
| Xi— 1 | 0-0,1 | 0,1-0,2 | 0,2 - 0,3 | 0,3 - 0,4 | 0,4 - 0,5 |
| Щ | |||||
| Xi | 0,5-0,6 | 0,6 - 0,7 | 0,7-0,8 | 0,8 - 0,9 | 0,9 - 1,0 |
| Tli |
При уровне значимости а = 0,01 проверить гипотезу До, состоящую в том, что с. в. X имеет равномерное распределение на отрезке (0,1] (вероятности pi определяются формулами рг — hi (i = 1,2,..., к),
где hi — длина г-го отрезка [xi-i, Xi] ~ —)•
2. Результаты наблюдений над с. в. X (рост мужчины) представлены в виде статистического ряда:
| Л" (рост) | [150 - 155) | [155 - 160) | [160 - 165) | [165 - 170) |
| щ (частота) | ||||
| Х(рост) | [170 - 175) | [175 - 180) | [180 - 185) | [185 - 190) |
| щ (частота) |
Проверить при уровне значимости а = 0,05 гипотезу Но о том, что с. в. X подчиняется нормальному закону распределения, используя критерий согласия Пирсона.
3. По данным упражнения 2 проверить гипотезу о нормальном распределении с. в. X, используя критерий Колмогорова.
Ответы к упражнениям
Раздел первый Глава 1
1.3
1) в = в ' п = в {а + Л) = а • в + а • в; 2) (Л + С) - (В + с) = = ЛВ+ЛС+ВС+С = ЛВ+ЛС+С = Л^В+С; 3)_Пусть ги? Л 4- В
+ т. е. Л + 5СЛ-5.
Аналогично убеждаемся, что + + Л =
а) ABC; б) ЛВС; в)_Л+В+С; г) Л-В-С; д) ЛВС; е) Л^С+ЛВС+ХВС; ж) ЛВС = Л + В + С. Л1Л2(Л3 + Л4 + Л5)Л6.
11.7
Из 90 двузначных чисел 9 имеют одинаковые цифры, т. е. п — 90, га =
= 90 — 9 = 81. Следовательно, р = ^ = 0,9. р = 0,01, так как m = 1, п = 10 • 10 = 100.
.8
5-4-3 = 60; 5-4-3 + 5- 4- 3-2 + 5- 4- 3- 2-1 = 300. 12 + 15 -f 7 — 34. 10 • 9 ■ 8 • 7 = 5040. (10 - 9 • 8)2 = 72О2 = 518400 или Л?0 94 - 6561.
| Л? |
| ю- |
= 12-11-10-9 = 11880. А\0 = 720. А\'А\-А1 = 120. Р5 • Р3 = 720; Р7 ~ 720 = 4320.
 Рис. 66
Рис. 66
|
2.112-7-16; 2520 — ■ Cf6.
3. а) С| = 56; б) С\2 ■ С$ = 6160.
4. С?6 • С? ■ С? или ^ = 135135.
5. А72 = 27 = 128 или 2 • 2 • 2 • 2 • 2 • 2 • 2.
6. б3 = 216. Это 234, 666, 165,....
7. А\ = 46 = 4096.
8. = Сд = Cg - ItI"! = 21-4 = 84.
9. Cg = Cf0 — = 45.
20. С4 = C64 = Cf = 15, 15 • P4 = 360.
21-a) 4! = 24; 6) ^rfhrrr = 336°-
22' 2! • 3! - 4! " 126°'
23' 91^3! = 400400 = " '
1.9
1. п = Л| = 84 = 4096 a)m = 8- 7- 6- 5 = 1680, Pl = «0,41; 6) m = 8,
P2 = Шб ~ °'°0195; B) m = h П = 1Ш ~ °0024-
2. n = C|e,m = C2-C|,p=-^-i« 0,000064.
C36
3. n = 7\, m = 6!-2,p=^ = |«0,29.
4. n = 5! - 120, т = 2- 2-1-1;р = ^ = 0,033....
5. a) p = ^ «0,573; б) p = * 0,36.
6. a) p = = A » o,08; 6) p = ^ «0,408.
7. Группа из 5 команд может быть выбрана Сf0 способами (вторая группа образуется автоматически), т.е. п — CfQ. В первую группу попадет либо один лидер, либо два. Стало быть, m = С\ • С4 + С| • С|. Поэтому
| 10. = 4! = 24 (один сел где угодно). 11.3-2-8! = 241920. |
р = ' +5 ' С' » 0,833. Сю
| С1 г>2 г1 о о р _ 4 ' °32, " О* 8. р _ —^---------------------- + °36 |
| ^36 |
0,21. Воспользовались свойством: Р{А + В)
= Р(Л) + АВ = 0. Здесь Л = одна дама, В = две дамы.
1.10
1. Сторона треугольника равна Ryfb. Значит, р = ^ = ^ R? = ss 0,41. ° ^
2. р = ~ = 0,32.
| 0,25. |
| 1. |
| 2. |
3. Обозначим длину I отрезка через ж, И — через у, тогда III отрезок имес длину I — х — у. fi = {{х,у}: 0 < х 4- у < Z}, т. е. 0 < х + у < I — вс возможные комбинации длин частей отрезка. Чтобы из них можно был составить треугольник, необходимо выполнение условий: х + у > I — х — i х + I - х - у > у, у + I - х - у > х, т.е. х < ^ у < х + у > Эт неравенства определяют область, заштрихованную на рис. 67.
 Рис. 67
Рис. 67
|
Имеем: Р =
1.15
Да. О = {1,2,3,4,5,6}, А = {2,4,6}, Б = {4,5,6}. Ясно, что Р(А) = | = ^ Р(Я) = I а Р(ЛВ) = | = i т.е. - | ^ • Р(В) = \ ■ ± =
а) А\ — первая буква Т, Л2 — вторая буква И,..., А5 — пятая букв. И. Вероятность события А — получится слово ТИСКИ, равна Р(А) = = P(AIA2A3A4A5) = 00004; б) Qi так каж рторо|
буквы К в слове СТАТИСТИКА нет; в) р = ^ • | • | = ш
qt ~ 0,2 — вероятность отказа г-го элемента, рг = 0,8 — вероятность ег< исправной работы. Цепь последовательно соединенных элементов 1-2-,
0,008
будет работать, если исправны все три элемента: р\2Ъ = P\'P2'Pz — 0,83 = = 0,512. Цепь параллельно соединенных элементов 5-6 отказов, только в случае отказа обоих элементов q^ = <7.5 <7б ~ 0,22 = 0,04, а вероятность ее исправной работы равна = 1 — q^ = 0,96, Р456 = Р4 ■ Р56 — 0,8 • 0,96 = = 0,768; Р123456 == 1 - 9123 • 2456 = 1 - (1 - 0,512) • (1 - 0,768) «0,887; Ротк = 1 -Р123456 -Р7 «1 - 0,887. 0,8 «0,291.
1.16
1. А — первый шар белый, В второй шар черный. Тогда АВ + АВ — оба
шара разных цветов. Р(АВ + АВ) =? + = 0,39.
У о У о IL 1о
2. а) А\ — попадание первого орудия, А2 — второго, Аз — третьего. Значит,
ABC 4- ABC + ABC = D — попадание только одного из них. P(D) = = 0,7-0,3-0,3-3 = 0,189; б) S - A1A2As — три промаха. P(S) = 0,3-0,3-0,3 = = 0,027. Значит, P(S) = Р{АГ + А2 + А3) = 1 - P{S) = 1 - 0,027 = 0,973.
3. Вероятность выхода из строя всех п приборов равна
(1 - 0,7) • (1 - 0,7) •... - (1 - 0,7) = 0,3П.
^i...... ^.и,....I. I.к...... ✓
л
Следовательно, вероятность безотказной работы равна 1 — 0,3П. По условию 1 - 0,3n ^ 0,95. Отсюда 0,3П < 0,05, п In 0,3 ^ In 0,05,
In 0,05: In 0,3 «2,488,
т.е. п^ 3. 1.18
1. А — вышла из строя одна микросхема, Hq — отказали обе, Hi — отказала первая микросхема, if2 — отказала вторая^ — обе не отказали.
Тогда Р{Н0) = 0,07 • 0,1 = 0,007, Р(Н{) = 0,063, Р{Н2) = 0,093, Р{Щ) = з
= 0,837 (Контроль: £ Р(Нг) = 1). Р(А\Щ) = 0, P(A\Ht) = 1, Р{А\Н2) = = 1, Р(А|Я3) = 0. Значит, Р(А) = 0,156 и Р{НХ\А) = 0,404.
on о
2. Ai — студент П сдаст экзамен, если зайдет первым, P(Ai) = ~ = А2 — студент П сдаст экзамен, если зайдет вторым, Р{А2) =? Введем гипотезы: Hi — первый студент вытащил билет, который знает студент П, Н2 — первый студент вытащил билет, который не знает студент П.
= I =!• = 1 = I (I + I = l). Далее: Р(А*\НХ) = f,
Р(Л2|Я2) = §. Значит, Р(Л2) = | ■ || + i ■ || = Все равно.
3. Пусть А — изделие пройдет контроль, Н\ — взятое изделие стандар'
но, Я2 — не стандартно. P(#i) = 0,9; Р(Я2) - ОД; P(A|#i) = 0,91
Р{А\Н2) = 0,06. Следовательно, а) Р(А) = 0,9 • 0,96 + ОД • 0,06 = 0,8'
0 0 ■ 0 96 б) 0,993.
1.20
1. а) Р10(4) = Cf0 • (i)4 • (i)6 «0,21; б) Р10(0) = Q)*0 и 0,00098; в) р = Pl0{ 1) + Рю(2) +... + Рю(10) = 1 - Рю(0) «0,999.
2.
Следует, что Р4(2) > Рв(3), т.е. 2 из 4.
3. а) Р3(3) - С| • 0,513 • 0,49° «0,133, б) Р3(1) = - 0,51 • 0,492 0,368.
4. Спички брались 2-10 — 6 = 14 раз, из них 10 раз из коробки, котора оказалась пустой. Имеем 10 «успехов» в 14 «испытаниях», т.е. Pi4(10) -
1.21
1. р = 1: 365 w 0,0027, п = 84, а ъ 0,23. По формуле Пуассона Р84(2) «0,232 ^,7945 и 0,021. (е~0'23 » 0,7945).
2. п = 200, р = 0,02. Значит, а — [пр] = 4. Искомая вероятность:
Р2оо(0) + Р20о(1) = + ^ » 0,09.
3. Здесь п = 100, т = 60, р = q — Используем локальную теорему Муав
ра-Лапласа: ж = 60 - 100 • 0,5_ = Рюо(60) = \ц>(2) = 0,2-0,054 я
У V100 • 0,5 • 0,5 V } $ К 1
^ 0,0108.
4. Р8оо(т, 800) = 0,95. Используем интегральную теорему Myавра-Лапласа
= т "у^^, х2 = 29. Значит,
Ф0Ы= 0,5; 0,5-Ф0 (3881~т) =0,95. Откуда Ф0 (388Х4 W) = 0,45, 388ц т = 1,65. Значит, т = 365.
Глава 2 2.2
1. Возможные значения с. в. X есть 0, 1, 2, 3, 4. Их вероятности равны соответственно: Р1 = р{х = о} = с4° • Q)0 • (±)4 = А, Р2 = = 1} =
2. Пусть Ai — первый студент сдает экзамен, А2 — второй сдает экзамен. С.в. X принимает три значения: 0,1,2. a) pi = Р{Х ~ 0} = Р(А\А2) = = 0,4 • 0,1 = 0,04; р2 = Р{Х = 1} = Р{АхА2 + АхА2) = 0,6 • 0,1 + 0,4 • 0,9 = = 0,42; рз = Р{Х = 2} = Р(АХА2) = 0,6 ■ 0,9 = 0,54 = 1); б) рх = = Р{Х ~ 0} - Р(А_ХАХА2А2) = 0,4 0,4-0,1 • 0,1 = 0,0016; р2 = Р{Х = 1} = = Р(АхА2А2 + AiAxA2 + А1А2А1А2 + АхАхА2А2) =... = 0,1668;
рз = Р{Х = 2} = P(AiA2 + AiA2A2 + АхАхА2 + AiA2AiA2) =
= 0,6 • 0,9 + 0,6 ■ 0,1 ■ 0,9 + 0,4 • 0,6 • 0,9 + 0,4 ■ 0,1 • 0,6 • 0,9 = 0,8316
(Eft = i).
»=1
2.3
Ах — попадание I стрелка, А2 — II. Тогда Р{Х = xi} = Р{Х — 0} = = Р{АхА2) = 0,08, Р{Х = х2} = Р{Х = 1} - P(AiA2 + АхА2) = 0,44, Р{Х = 2} = 0,48.
ГО,
F(x) — i O5O8, 0 < х ^ 1; w | 0,52, 1 < х < 2; [l, 2<х.
F(x) удовлетворяет свойствам функции распределения;
Р{0 < ж < 1} = F(1) - F(0) = 1 - е"1 = 1 - \ » 0,632.
Р{Х е (0,1)} - F(l) - Р(0) - Значит, Р4(3) = С43 • (±)3 • = 0,25.
2.4
1. F(2) = 1. Значит,
(2(х + 1) ^
9 [О, 2].
2. 5Д = ± • = 1. Значит, ОМ = Л = 4. Уравнение MJV: | = f—т.<
2 _ 0
у = —8а; -f- 4. Стало быть,
f{x) = <,) U
| = / 0 oft = 0; |
О, xi (0;±j;
если х ^ 0, то
X
F(x)= J
если 0 < х ^ то
0 х
F(s) = J Qdt + J {-St + 4 )dt = -4x 2 4- 4z;
-oo О
если x > то
= J 0dt +J(-8t + 4)dt +J 0dt = l,
-oo 0 1
таким образом
0, я О,
i?(ar) = J ~4х2 + 4х, 0 <х ^
1,
? = J(-8х + 4)dx + JOdx = I.
l l 4 2
oo
3. а) нет, так как /(x) ^ 0 при x £ f-oo,0); б) да, f(x) > 0, J f(x)dx = 1
—oo
00 0 2 oo
| г о = 1, a - Есл: О о |
в) J f{x)dx= J Odx +J ax2dx +J Odx = 1, т. e.
-oo -oo 0 2
3 4
a = q, то /(ж) — плотность распределения; а ф f — нет. о о
2.5
Учитывать результаты примера примера 1.31 (п. 1.20) в первом случае имеем: MX = 0 • 0,001 + 1 • 0,027 + 2 • 0,243 + 3 • 0,729 = 2,7; во втором случае: MX = 0 • 0,006 + 1 • 0,092 + 2 • 0,398 + 3 • 0,504 - 2,4.
ОО 0 7Г ОО 7Г
MX = xj(x) dxj = J x-Odx+J ^xsmxdx+Jx-Odx = ^ Jxsinxdx =
— oo — OO О 7Г 0
— ZL 2'
3. Согласно свойствам м. о. и дисперсии, имеем MZ = М(5Х — ЗУ + 2) = = М5Х - МЗУ + М2 - 5M.Y - ЗМУ + 2 = 5-2-3- (-3) + 2 = 21 и DZ = D(bX ~ ЗУ + 2) = Я5Х + D(-ZY) + D2 = 25£>Х + 9/?У + 0 = -25-2 + 9-9 = 131.
ОО 0 1Г оо
4. = ^J x2f(x)dx-{MX)2 = j x2-0dx + J x2-±sinxdx +J x2-0dx-
— OO —OO 0 7Г
n
— = ^ J x2 s'mxdx ~ = x2 cosx ^+2 ^xsinx|o + cosx|ojj -
5. Если x Л, то F(x) 0, lim 0,25x2 = 0, т.е. 0,25Л2 = 0, A = 0;
V ' x-tA+0
lim 0,25x2 = 1, т.е. 0,25B2 = 1, В = 2. Поэтому
x-tB
Г0, при x ^ 0,
j?(x) = < 0,25x2, при 0 < x < 2, [ 1, при 2 < x.
Тогда
, _ Г0, при х ^ 0 и х > 2, 7 w — |о,5х, при 0 < х < 2.
Поэтому
2 2 MX = J X • 0,5xdx = 4/3, DX - J X2 ■ 0,5xdx - = |. о о
Значит, ax —
6- = = йХ> = + » + + = n
^ ' i=l i=l n
| _ 2 cr2 |
( П v. / П \ П П
n na = a;
2.7
1. Р{-3 < X < 5} = Ф0 - Фо = Фо(1) + Фо(3) = О,
Р{Х < 4} - Р{-оо < X < 4} = Ф0 - Фо (~°°2~3) = Фо(0,5)
+ Фо(оо) = 0,19146 + 0,5 = 0,69146; Р{\Х - 3| < 6} = Р{\Х - 3| < 3 • 2} = 2Фо(3) = 0,9973.
2. По условию а = 0, <7 = 1 а) Р{Х <Е (1,3)} = Ф0 (^у^) (^у^)
= Ф0(3) - Ф0(1) = 0,49865 - 0,34134 = 0,1573; б) 2Ф0 = 0,8926, отсну
Фо (0 = 0,4463. По таблицам находим, I = 1,62, и интервал имеет в* (-1,62; 1,62); в) М0Х = 0\ Ме = 0.
3. Коэффициент асимметрии А нормального распределения равен 0 {А — 0 так как кривая Гаусса симметрична относительно прямой х = а, проход: щей через центр распределения а. Найдем (аналитически) коэффициеь эксцесса, т. е. Е = ~ — 3. Сначала найдем /х4:
и = х3
dv — хе 2<г2 dx
| = —Lf-sVe"^ оу2тг \ |
| +3(7' |
| (- |
| хе 2о-2 а2 |
| / е dx = |
| 0 + 3 а' |
| (Т\/27Г \ |
оо
J х2е 2а2 dx^j
-оо
| оо / |
| du = Зж2 dx |
| е 2 о-2 dx = |
| /i4 = |
| X |
| -л/2тг |
| v = —а2е 2сг2 |
оо 0 /
—оо
00 /д. \ 2
| V2cr |
= —(зсг2 ^0 + ct W2 J d
Стало быть: Е = - 3 3-3
<7
= = За
СГ1/27Г
Глава 3
3.3
оо оо оо оо оо
1.1) J J f{x,y)dxdy = 1. Поэтому A J J е~х~у dxdy = A J е~х dxx
-оо -оо 0 0 0
оо оо оо
х J е~у dy = A J е~х dx = A j е~х dx = А = 1. 2) F(x,y) =
0 0 о
х у х у х
= / / e ~ U ~ Vdudv = / e~Udu / e~"dv = / e~U (_е~1о) = ~ 0 0 0 0 о
X
х J е~и du = (1 - е-аг)(1 - е_г/) при ж ^ 0, у ^ 0, т. е. о
| 0, |
' (1 - е~*)(1 - при х > 0, у ^ О,
Fx,У -
в противном случае.
X ОО X ОО X
| 3) Fx{x) |
| 0 0 |
J i^j f{x,y)dyjdx = J (^J e~ue~vdvjdu = J 1 • e~u du =
— oo —oo
= 1 — e xi при x ^ 0, т. e.
Аналогично
[^U, пр
^.М-ЛМ^ВД»!'1-0' приоо> = |р
[0, при х < 0, [0,
I f>~У гти и П
Аналогично, /у (у)
5) > 0,У < 1} = J e~xdx J е~у dy = -(е-1 - 1) J е~х dx =
0 0 о
| 1 — e при ж ^ 0, О, при х < 0. 1 - еГу, при у > 0, 0, при у < 0. (1 — e~x)f, при 0, при е-у, при у ^ 0, 0, при у < 0. оо 1 |
| Fx |
| при х ^ 0, при я; < 0. |
= (!-!) (е-)^ 1-|-0,63.
оо оо 4 4-х 4
| dx = 1, О = q. |
!. 1) J J f{x,y)dxdy = 1, т.е. J dx J С dy = 1, С J (4 - x)
о 0
, при x > 0, у > 0, x + у ^ 4;
Следовательно, /(ж, у) ~ < 8
I 0, в противном случае.
4-х
J f(x,y) dy - J = ®G(0,4), /у(у) =
-oo 0
| 2) Мх) = 4-у |
, 0 < у < 4; 3) P{0 < X < 1,1 < Y < 3} = JJ f(x,y)dxdy =
Dx
1 л
= | J dx J dy = 0,25 (см. рис. 68).
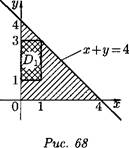
|
3. 1) С. в. X принимает значения 0, 1, 2. Очевидно, p\ = P{X = 0} — 0,6 0,6 — = 0,36, p2 = 0,4 • 0,6 + 0,6 • 0,4 - 0,48, pz = 0,4 ■ 0,4 - 0,16. Стало быть:
| р | 0,36 | 0,48 | 0,16 |
з
(У^Рг ~ 1). Аналогично находим, что х=1
| У | |||
| Р | 0,16 | 0,48 | 0,36 |
есть ряд распределения с. в. Y. 2) Возможные значения системы (X, У): (0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2). Совместная таблица
распределения имеет вид:
| X\Y | |||
| 0,0576 | 0,1728 | 0,1296 | |
| 0,0768 | 0,2304 | 0,1728 | |
| 0,0256 | 0,0768 | 0,0576 |
так как рп = Р{Х = О, У = 0} = 0,4 • 0,4 ■ 0,6 ■ 0,6 = 0,16 • 0,36 = 0,0576, Р12 = Р{Х = О, У = 1} = 0,36 • 0,48 = 0,1728, р13 - Р{Х - О, У = 2} = = 0,36 • 0,36 = 0,1296, p2i = Р{Х = 1,У = 0} = 0,48 • 0,16 = 0,0768, Р22 = Р{Х = 1,У = 1} = 0,48 • 0,48 = 0,2304, р23 = Р{Х = 1,У = 2} = = 0,48 • 0,36 = 0,1728, р31 = Р{Х — 2,У — 0} — 0,16 • 0,16 - 0,0256, Р32 - Р{Х = 2, У - 1} = 0,16 • 0,48 - 0,0768, р33 - Р{Х = 2, У = 2} = = 0,16-0,36 = 0,0576. 3) По таблице распределения, пользуясь равенством F(x>y) — ^^ Pijy находим значения функции распределения F(x,y):
Xi<X yi<y
| X\Y | У <0 | 0 <y < 1 | 1 <У <2 | У> 2 |
| x < 0 | ||||
| 0 < x < 1 | 0,0576 | 0,2304 | 0,3600 | |
| 1 < x < 2 | 0,1344 | 0,5376 | 0,8400 | |
| ж > 2 | 0,1600 | 0,6400 | 1,0000 |
3.7
1. Имеем
| X | и | У | |||||||
| P | 0,33 | 0,33 | 0,34 | P | 0,24 | 0,28 | 0,27 | 0,21 |
Тогда тпх = 1 ■ 0,33 + 2 ■ 0,33 + 3 • 0,34 = 2,01, ту = 1 ■ 0,24 + 2• 0,28 + 3 • 0,27 + + 4 • 0,21 - 2,45. Так как
Р{Х = 1, У = 1} = 0,07 ф Р{Х = 1} • Р{У = 1} = 0,33 • 0,24 = 0,0792,
то с. в. X и У — зависимы. Находим МХУ: МХУ = 1 • 0,07 + 2 • 0,04 + + 3-0,11+4-0,11+ 2-0,08+4-0,11+6-0,06+8-0,08+3-0,09 +6-0,13 + 9-0,10 + + 12 • 0,02 = 4,71. Поэтому cov(Х,У) = 4,71 - 2,01 • 2,45 = -0,2145.
JJ f(x,y) dxdy ~ 1, поэтому
11 1 4 1
a J dx J(1 — xy^)dy — a J dx ^y — | ^ — a J 2 dx ~ Aa = a =
i L
MX = ^J xdx J (1 ~xy3)dy =... = 0,
-l -l l l l
MY^ifdxJ y{l-xy*)dy = \ J dx(^-x^j
-l -l -l l l
| -l |
| 1 1 |
DX=\ J(x-0)2dx J(l-xy3)dy =...^±,
-l
значит, <jx =
л/3
| = 1 3 & л 4 5* 2 |
oo oo
DY -
J J {y-my)2f(x,y)dxdy = ± J dx Jy2(l~xy3) dy -...
— oo —oo
значит, av =
Уз
^хк = \ff хУ(г ~ ХУЪ) dxdy ~ 0 = ■ • ■ = ~ i^- -l -l
__ L
Следовательно, rxv ~ ~[—= —
Vs V3
l l
I. с J dx J(x + y) dy — 1. Отсюда с = 1. Находим плотность вероятность
/lM = J(х +у) +
о
/гЫ= + У) dx = ^ + yrrj у + i о
Так как /х(х) ■ f2(y) = + + Ф х + у = /(гс,у), то с. в. X
1 1 1
| -1 -1 |
| 1 1 |
| 0 0 |
| зависимы. |
MX = J xdx J(х + у) dy = J х (х + dx =
MY = — 12'
| 11 144 |
| DX |
= J ~ 12) dx J{x +у) dy =
или
1 1
DX = J x2dx J(x + y)dy-^y =
| 0,10 0,25 |
144'
3.9
| 25 25 |
| = % РЫУ2) = Щ Значит, M(X|y2) = 0 • + 1 ■ § = |
1. Найдем условное распределение X: p(xi|yi) = P{X = 0|У = —1} =
= рыух) = Щ = Значит, М(Х|У1) = 0 • щ + i. If = 1| = 0,6.
0,15
p(zi\V2)
0,40 40'40* — v-i^/ - 40 25 _ „..о „/„ \ _ 20... \ 15 о U/vl л _ 15
= |g «0,63. p(®i|y3) = рЫуз) = Значит, Af(X|y3) = Щ «0,43. Кривая регрессии X на у имеет вид, изображенный на рис. 69.
i+

|
0,43
-1
Рис.
2. Как известно, для нормально распределенной с. в. (X, У) ее составляющая У также распределена по нормальному закону (формула (3.37)):
(У -ту)2
/2(y) = rfee~ •
<Jy V 27Г
| /ОФ) - |
Имеем
/(g>y) = 1 с~2(1-г2)(х2~2ГЗГ1/+у2). =
| DY = |
/2 (у) 27гл/1 - г2 ' л/2тг
V2k -\fl - г2
т. е. условная плотность распределения f(x\y) есть плотность нормальн распределения с параметрами т = у г и сг = \/1 — г2. Аналогично наход что
| (х — уг |
// \ (у~хг)2
f{y \ x ) = 1Щ1 = 1.
/lM v^Wl - г2
| 3.11 1. Так как |
| , х?[а,6], |
10, х£[а,6],
то
о
М = rb / = rb ■ - eita> = -
2. Так как р* = Q*e, Q, /с = 0,1,2,..то
00 А- л 00 (nJ-t\k
^(t) = £ j*9£fil = £ iili. = е- • e-lt = е-*1-"*.
к\ ^ к! к= 0 fc-0
Тогда (ft(t) = е-в(1"е")-(-а)-(-е")-г, значит, MX = [-гУ(О)] - -t-(l-m = а, т. е. MX = а.
-1 0 оо 0
L = J jtx • 0 dx + J eitx{-2 x)dx + J eitx • Odx = -2 J eitxxdx
-oo -1 0 -1
= _2 (-1 • ±eH° ^ = "2(0 " + 4(1 " = ^
\it Ui it si |-i J v it t2 *
_ 2, 2e~u = - 2 + 2e~^
i2 t2 t2
Глава 4 4.1
| У | -3 | -1 | ||
| p | 0,30 | 0,45 | 0,20 | 0,05 |
| У | V2 | V5 | ||||
| р | 0,10 | 0,20 | 0,30 | 0,25 | 0,10 | 0,05 |
| У | Уз 2 | ч/З 2 | ||||
| р | 0,3 | 0,35 | 0,35 |
| б) в) |
| 2. |
| У | ||
| V | 0,5 | 0,5 |
Многоугольники распределения с. в. X и У изображены, соответственно, на рис. 70, 71.
 Рис. 70
Рис. 70
|
MY = 0 • 0,5 +1 • 0,5 = 0,5; DY = [MY2 - (МУ)2] = О2 • 0,5 +12 • 0,5 - (0,5)2 = = 0,5 - 0,25 = 0,25. Отсюда <тУ = s/Ш = v/p5 = 0,5. 3. С. в. X имеет равномерное распределение, значит,
\о, xi[-2,2].
Функция у =:с + 1 строго возрастает в (—оо,оо), обратная функция х = у - 1 = Vfo), У? [-1,3]. По формуле р(у) = /(ф(у)) • \ф'(у)\ находим:
[0, у i [-1,3],
т. е. У ~ R[-1,3]. Находим МУ: МУ - J ^dy = 1 (или МУ = М(Х +1) =
-1
2 3
 Рис. 71
Рис. 71
|
= J(x + l)-±dx = l). DY = МУ2-(МУ)2 = J^dy-12 = <тУ =
1 ——
4. По условию fx(x) — ____ е 2. а) Функция у = Заг имеет обратную
v 2 7г
х= \j\ = ^Ы, = = • Поэтому
1 1 _!?/? (?(у) = • — j=e 2V9, у^О.
V2?r Зд/Зу2
б) у = |х| = х < о' обратная функция для у = |х| есть
х\ = —у = ipi(у). На [0,оо) обратная функция есть х2 = у ~ Ф2{у)- Стало быть,
9(У) = £/«>,(y))W<(v)l = • 1 + • 1 = -j^e'T,
v27T Л/2ТГ у2тг
у? [0, оо).
5. а) По условию f(x) = е-ж, ж) 0 и Р(х) — 1 — е~х, х ^ 0. <3(у) = - Р{У < у} = Р{2Х-1 < у} = = + l
у + 1
— 1-е 2, у ^ —1 (так как условие х ^ 0 переходит для у = 2а; - 1
__у±1 / 1 \
в условие у ^ -1). Следовательно, д{у) — G'{y) = -е 2 / — 1 _У±1
= 2е 2 ПРИ У > -1 = 0 ПРИ У < б) Если У ^ т0 ^fe) =
= Р{У < 0} = 0 и 5(у) = G'(y) = 0. При у > 0 имеем G(y) = Р{У < у} = = Р{Х2 < у} = Р{|Х| < уу} = Р{-^у < X < у/у] = Р{0 < X < уу} = = Р{Х < ^у}-Р{Х < 0} = P(v1/)-P(0) = (1——(1—е°) = l-e^, у > 0. Тогда д(у) = Gf(y) = (1 - e^K - • е"^, т. е.
1 У> о,
</(у) = { W
[0, у< 0.
ОО 0 ОО 00
Контроль: J 0(y)dy = l, J 0 • dx + J = - J e~^d(-y/y) =
—00 —00 о 0
= —e = — (0 ~ 1) = 1. (Иначе: при x G (0,00) имеем x = ^/y = V'(y)-
Поэтому g(y) - /(^y) • (^/у)'у = e"^ • у > 0.)
4.2
1. Находим F x +y(z). F{z)= Р{Х+ Y < z} = JJ {х + у) dxdy. F{z) = О
Dz
(х + у < г)
при при 0 < z ^ 1 (на рис. 72 область Dz заштрихована вертикаль
ными линиями) имеем
| x)2\ |
| 2 (Z ~ zx — x Л----------------- ~ |
z z—x
F[z) = j dx j (x + y)dy = у (
| o" 3Z ' |
zx2 x [6] . (x-zf 2 3 6
при 1 < z ^ 2 (область Dz заштрихована горизонтальными линиями) имеем
z—l 1
J dxj{x +у) dy+ J dx J (яг + у) dy
0 0 2-1 о
г—1 1
= /(*+!)d*+/(
| F(z) = |
| zx2 хг jx-z) 2 3 6 |
= (т + |) Г+ 11 =h-z* + 3z2-l),
| 2 (z - x)' xz — x H------ r---- I dx = |
2-1 О
Итак,
| Г0» 3 ' |
| F(z) = |
0 < z < 1,
|(-z3 + 3z2-l), 1<Z<2, U, z > 2.
Отсюда
0, z ^ 0, или z > 2,
| f(z) = F'(z) |
2z - z2, 1 < 2 < 2.
У = z - х

|
5. F(z) = Р j-^r < zj = J {х + у) dxdy. F(z) — 0 при z < 0; при 0 <
Dz

| у = ZX |
| Рис. 73 |
имеем
1 zx
| _ z, z_ з^б- |
| о 0 |
F(z) = J dx J{x + y)dy При 1 < z < oo имеем
z xz
F(z) = J dx J{x + y)dy + J dx J{x + y)dy = 0 0 10
Следовательно,
| ro, 3 ' 3 |
| no = /(*) = 4 |
Z < 0, i + l, o<2<i,
oo 1 oo
Контроль: J f{z) dz = J + §) dz+ j f + J dz = 1 (см. рис.
-ОО
Глава 5
5.5
| 2 2 = 1 - |
| DX |
| 125 502 |
1 _ 0,05 - 0,95; б) с.
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-02-12 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |