Лабораторные работы
По курсу
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫЭЛЕКТРОТЕХНИКИ»
Линейные электрические цепи в синусоидальном режиме
Второе издание, дополненное
Новочеркасск 2007
УДК 621.3.01(076.5)
Рецензент – канд. техн. наук В.А. Плаксин
Составители: Ершов Ю.К., Птах Г.К., Саввин Д.Д., Кирсанов А.Г.,
Олейникова Л.В., Семенченко А.И.
Лабораторные работы по курсу ″Теоретические основы электротехники″. Линейные электрические цепи в синусоидальном режиме. 2-е изд., доп. /Юж.-Рос.гос.техн.ун-т. Новочеркасск: ЮРГТУ, 2007. - 34 с.
Приведены программы и рекомендации по исследованию установившихся синусоидальных режимов однофазных и трёхфазных линейных электрических цепей.
Предназначены для студентов, изучающих курсы «Теоретические основы электротехники» и «Основы теории цепей».
© Южно-Российский государственный
технический университет (НПИ), 2007
© Ершов Ю.К., Птах Г.К., Саввин Д.Д.,
Кирсанов А.Г., Олейникова Л.В.,
ЛАБОРАТОРНАЯ РАБОТА №7
ЦЕПЬ r, L, C В СИНУСОИДАЛЬНОМ РЕЖИМЕ
Цель работы: освоить измерение параметров цепи синусоидального тока и построение векторных и временных диаграмм.
Программа работы.
1. В данной цепи с последовательным соединением резистора и конденсатора (рис.1) измерить ток и напряжение на всех участках. Рассчитать параметры r, C. Построить векторный треугольник напряжений и тока, треугольник сопротивлений, графики i (t), u (t)
| I | U | U r | U C | z | R | x C | C | ||||
| дел | А | дел | В | дел | В | дел | В | Ом | Ом | Ом | мкФ |
Расчетные формулы:
,,,,,,,,,
2. В цепи индуктивной катушки (рис. 2) измерить ток, напряжение и активную мощность. Рассчитать параметры r к, L. Построить векторный треугольник напряжений, треугольник сопротивлений и графики i (t), u (t)

| 
| |
| Рис. 1. Последовательное соединение резистора и конденсатора | Рис. 2. Схема для определения параметров r к и L индуктивной катушки |
| I | U | P | z к | r к | x к | L к | U а | U р | φ r | |||
| дел | А | дел | В | дел | Вт | Ом | Ом | Ом | Гн | В | В | град. |
Расчетные формулы:
,,,,,,,,,,
3. В цепи с последовательным соединением резистора, индуктивной катушки и конденсатора (рис. 3) измерить ток, активную мощность и напряжение на всех участках. Построить векторную диаграмму напряжений и совмещенный с ней треугольник сопротивлений.
| I | P | U | U r | U к | U C | z э | r э | x э | ||||||
| дел | А | дел | Вт | дел | В | дел | В | дел | В | дел | В | Ом | Ом | Ом |
Расчетные формулы:
,,,
4. В цепи с параллельным соединением индуктивной катушки и конденсатора (рис. 4, ключ К разомкнут) измерить входные ток, напряжение, активную мощность, а также токи в ветвях. Построить полную векторную диаграмму токов и напряжений. Определить величину угла φэ.

| 
| |
| Рис. 3. Схема для исследования последовательного соединения резистора, индуктивной катушки и конденсатора | Рис. 4. Схема для исследования параллельного соединения индуктивной катушки и конденсатора |
| U | P | I | I 1 | I 2 | I ' | ||||||
| дел | В | дел | Вт | дел | А | дел | А | дел | А | дел | А |
5. Считая цепь (рис. 4) пассивным двухполюсником, определить знак угла φэ, измерив входной ток I 1 при подключенной емкости C ' (ключ К замкнут) и, сравнив его с входным током I, измеренным при отключенной емкости C ' (ключ К разомкнут).
Используя измеренные на входе двухполюсника U, I, P (п. 4), рассчитать эквивалентные сопротивления z э, r э, x э последовательной схемы замещения проводимости y э, g э, b э параллельной схемы замещения.
6. Рассчитать для цепи (рис. 4) z э, r э, x э и y э, g э, b э, считая заданными параметры катушки r к, L и емкость С конденсатора, «свернув» цепь относительно входных зажимов. Сравнить результаты опытного (п. 5) и аналитического (п. 6) расчетов.
Пояснения к работе
Резистор и конденсатор на низких частотах можно считать физическими носителями «идеальных» параметров: активного сопротивления r и электрической емкости C соответственно. При последовательном соединении r, С (рис. 1), когда доступны зажимы резистора и конденсатора, для измерения параметров достаточно иметь вольтметр и амперметр.
Индуктивная катушка обладает активным сопротивлением r к и индуктивностью L. На низких частотах катушку представляют последовательной r, L ‑цепью (рис. 2). Однако в этой цепи, в отличие от цепи, изображенной на рис. 1, для измерения имеются только входные зажимы. Параметры r к, L вычисляются по измеренным напряжению, току и активной мощности.
Измерение параметров цепи переменного тока с помощью вольтметра, амперметра и ваттметра является одним из самых распространенных методов. Этот метод применяется для определения эквивалентных параметров сложных пассивных цепей. Пассивный двухполюсник при фиксированной частоте может быть представлен схемой замещения из двух элементов: эквивалентного активного сопротивления r э (либо активной проводимости g э) и эквивалентного реактивного сопротивления x э (либо реактивной проводимости b э). Сопротивления r э, x э используются в последовательной схеме замещения, а проводимости g э, b э – в параллельной схеме замещения.
По измеренным U, I, P на зажимах двухполюсника (рис. 4) определяются z э, r э, x э или y э, g э, b э:
;;
;;
В выражениях для x э и b э корень берется в арифметическом смысле, т.е. эти формулы определяют только модуль, а не знак алгебраических величин x э и b э.
Для определения знака реактивного сопротивления (проводимости) необходимо выполнить дополнительный опыт с подключением на вход двухполюсника известного реактивного сопротивления (см. указания к п. 5 программы).
Наряду с приведенными выше формулами для нахождения r э, x э и g э, b э часто используют следующие выражения:
;
;
где.
Нетрудно видеть, что знак фазового угла φэ также не определен:, а значит, не определены и знаки x э и b э. в измерительной технике имеются приборы фазометры, которые измеряют величину и знак угла φ. При наличии фазометра по измеренным U, I, φ однозначно определяются все параметры, и надобность в проведении дополнительного опыта отпадает.
Методические указания.
Каждый пункт (за исключением последнего) программы лабораторной работы содержит измерения и расчеты, которые целесообразно сводить в одну таблицу. Образцы таблиц приведены рядом с соответствующей схемой. Все графики и диаграммы должны быть вычерчены на миллиметровке с указанием масштабов величин.
К пунктам 1 – 3. Опыты следует проводить при токах 1 – 2 А. Измерение напряжений на участках цепи осуществляется поочередным подключением одного и того же вольтметра. При измерении малых мощностей, когда показания ваттметра снимаются в начале шкалы, целесообразно устанавливать такое напряжение, чтобы ваттметр показывал целое число делений – это увеличивает точность отсчета.
К пунктам 4, 5. Измерение токов I, I 1, I 2 проводится одним и тем же амперметром, включенным поочередно в каждую ветвь цепи (рис. 5,а).
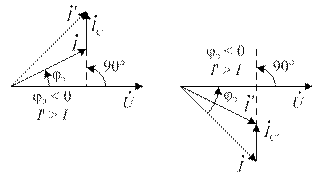
Определение знака угла φэ для двухполюсника (рис. 5,а) проводится сравнением величин I и I ' входного тока, измеренных соответственно при отключенной и включенной небольшой емкости C ' (рис. 4). Если при подключении C ' входной ток увеличился (т.е.), то, и двухполюсник имеет емкостный характер, если же I ' меньше I, то, т.е. двухполюсник имеет индуктивный характер. Это поясняется векторными диаграммами (рис. 5,б).

| 
| |
| а) | б) | |
| Рис. 5. векторные диаграммы, иллюстрирующие определение знака угла φэ пассивного двухполюсника путем подключения к его входным зажимам конденсатора небольшой емкости C ': а – схема пассивного двухполюсника, б – векторные диаграммы для и |
К пункту 6. Сворачивание цепи проводится в последовательности, указанной на рис. 6.
Параметры схем (рис. 6) определяются по формулам:

| Дано: r к, x к, x C Определить: r э, x э, z э | ||

| 
| 
| |
| а) | б) | в) | |
| Рис. 6. последовательность определения входных параметров (r э, x э) параллельного соединения индуктивной катушки и конденсатора: а – схема цепи; б – параллельная схема замещения; в - последовательная схема замещения. | |||
а),
,
;
б),,
;
в),
.
Последние две схемы на рис. 6 соответствуют случаю, когда двухполюсник имеет активно-индуктивный характер.
Контрольные вопросы.
1. Почему для определения параметров r, C в схеме (рис. 1) потребовались только вольтметр и амперметр, а для определения параметров r к, L индуктивной катушки (рис. 2) необходим еще и ваттметр?
2. Предположим, что цепь (рис. 1) помещена в непроницаемый ящик, из которого выведены только входные зажимы. Объясните опыты по определению эквивалентных параметров этого двухполюсника.
3. На входе двухполюсника напряжение и ток изменяются по закону;. Постройте графики u (t), i (t) и векторную диаграмму  ,
,  .
.
Вычислите активную мощность.
4. Для условия задачи 3 определите параметры последовательной и параллельной схем замещения двухполюсника.
5. В цепи (рис. 4) при разомкнутом ключе заданы:,,.
Найдите g э, b э и r э, x э для частот,,,,, объясните полученные результаты.
ЛАБОРАТОРНАЯ РАБОТА №8
ИССЛЕДОВАНИЯ ФАЗОВОГО РЕЗОНАНСА В ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ r, L, С
Цель работы: экспериментальное исследование явления резонанса напряжений, ознакомление с его практическим использованием при испытании изоляции кабеля.
Программа работы
1. Собрать цепь, изображенную на рис. 7. Увеличивая зазор в сердечнике индуктивной катушки, провести 7-8 опытов при различном состоянии цепи, включая и резонансный режим. Опыты проводятся при неизменном входном напряжении. Результаты заносятся в таблицу.

|
| Рис. 7. Последовательный резонансный контур |
| № опыта | Измерено | |||||||||||
| U | I | P | U р | U к | U C | |||||||
| дел | В | дел | А | дел | Вт | дел | В | дел | В | дел | В | |
| Вычислено | ||||||||
| z э | r э | cos φ | r р | z к | r к | x к | x C | φ |
| Ом | — | Ом | град | |||||
ВНИМАНИЕ! Для предотвращения опасно больших напряжений на реактивных элементах лабораторного стенда нельзя устанавливать входное напряжение выше 50 В.
2. По данным опытов п. 1 рассчитать эквивалентные параметры z э, r э, φ цепи, сопротивления резистора r р и конденсатора x C, а также параметры z к, r к, x к катушки. Вычислить добротность Q контура в резонансном режиме. Начертить в масштабе векторные диаграммы напряжений для трех состояний цепи:,,.
3. Собрать цепь, изображенную на рис. 8. Настроить цепь в резонанс при входном напряжении 10 В. По показаниям приборов в резонансном режиме определить добротность цепи. При каком минимальном напряжении сети данная схема позволяет получить испытательное напряжение 5 кВ?

|
| Рис. 8. Схема испытания изоляции кабеля. |
Пояснения к работе
В данной работе изучается явление фазового резонанса в последовательном контуре r, L, C. При резонансе напряжение на входе контура совпадает по фазе с током, т.е.. Это условие фазового резонанса через параметры последовательного контура записывается в виде:
или,
где – резонансная частота.
Из условия (1) видно, что настраивать последовательный контур в резонанс можно измерением параметров L, C или частоты входного сигнала. При резонансе сопротивление цепи минимально (), а ток максимален (опыты проводятся при неизменном входном напряжении), что позволяет по амперметру определить момент наступления резонанса.
При резонансе отношения называют добротностью контура. Через параметры контура добротность определяется следующим образом:
где – характеристическое сопротивление контура.
В реальных устройствах, кроме самого контура, потери могут возникать во внутреннем сопротивлении источника, а также в нагрузке, присоединяемой к контуру. Поэтому сопротивление r в формуле (2) должно быть увеличено на соответствующую величину, вносимую внешними элементами, что приводит к снижению результирующей добротности.
В момент резонанса вся энергия, поступающая от источника, расходуется в сопротивлении r контура, энергия же электрического поля переходит в энергию магнитного поля катушки и наоборот. Резонансные цепи очень широко применяются в электротехнике и представляют собой неотъемлемую часть всякого радиотехнического устройства. Однако следует иметь в виду, что в электротехнике резонанс напряжений часто является аварийным режимом. Исследование резонансных режимов в электрических цепях заключается в определении частотных характеристик, т.е. зависимостей различных величин (U, I, z, φ и т.д.) от частоты или нахождения зависимости этих величин от параметров L и C, а также в рассмотрении энергетических соотношений при резонансе.
В настоящей работе исследуются зависимости напряжений, тока, угла φ от L цепи и рассматривается пример использования явления резонанса напряжения для испытания изоляции кабеля.
Методические указания
К пунктам 1,2. Перед началом опытов сердечник катушки должен быть вдвинут (зазор равен нулю). Затем, выдвигая сердечник, необходимо при различных зазорах (зазор фиксировать не надо) его провести 3-4 опыта в дорезонансном режиме (), при зафиксированном резонансе (), и 3-4 опыта в послерезонансном режиме (). При проведении опытов напряжение на входе цепи должно поддерживаться неизменным. По данным опытов рассчитываются входные параметры цепи:
;;
и сопротивления отдельных участков цепи. В схемах опытов в качестве индуктивного элемента используется катушка с выдвижным сердечником. Катушка обладает индуктивностью L и активным сопротивлением r к, так что общее активное сопротивление цепи равно, где r р – сопротивление резистора. Непосредственно измерить активную  и реактивную U L составляющие напряжения катушки нельзя. Однако по измеренному току, активной мощности всей цепи и напряжением на участках эти составляющие легко вычислить:
и реактивную U L составляющие напряжения катушки нельзя. Однако по измеренному току, активной мощности всей цепи и напряжением на участках эти составляющие легко вычислить:
;;  ;
; 
После выполнения расчетов строятся в масштабе на миллиметровке графики и векторные диаграммы. При этом зависимости I (x к), U L(x к) и U C(x к) необходимо строить в одних осях координат. При построении графиков величину x к можно брать равной z к, а U L равной U к, так как.
По данным опыта строятся три векторные диаграммы напряжений: по одной для дорезонансного (), резонансного () и послерезонансного () режимов. Для построения векторных диаграмм следует предварительно рассчитать  и U L.
и U L.
К пункту 3. Явление резонанса напряжений представляет практический интерес, так как на отдельных участках цепи может происходить значительное повышение напряжения.
В опыте п.3 резонанс напряжений используется для получения от низковольтной сети высокого напряжения, необходимого для испытания изоляции кабеля. В лабораторном стенде кабель имитируется конденсатором (при испытании изоляции потерями и ЭДС самоиндукции кабеля можно пренебречь).
Контрольные вопросы
1. Почему в момент резонанса цепи (рис. 7) напряжение на катушке больше напряжения на конденсаторе?
2. Что такое добротность контура, как она вычисляется через параметры контура?
3. При каких условиях напряжения на реактивных элементах цепи (рис. 7) могут превышать входное напряжение?
4. Контур (рис. 7) настроен в резонанс, останется ли он в резонансе, если конденсатор шунтировать активным сопротивлением R? Как при этом изменится эквивалентная добротность? Ответ обосновать.
5. Приведите примеры практического приложения явления резонанса напряжений.
ЛАБОРАТОРНАЯ РАБОТА №9