Цель работы: освоение экспериментальных способов определения параметров r, L, M и исследование влияния магнитной связи на эквивалентные параметры цепей.
Программа работы
1. Ознакомиться с основными теоретическими положениями, применяемыми при описании электрических цепей с магнитной связью, по рекомендованной литературе и пояснениями к настоящей работе. Объяснить, а если необходимо, вывести содержащиеся в пояснениях формулы.
2. Собрать цепь (рис. 14) и по измерениям определить активное сопротивление r и индуктивность L каждой из двух катушек на частоте 50 Гц.
|
| Рис. 14. Схема для измерения параметров катушки |
3. Для заданного расположения катушек произвольно промаркировать их зажимы и определить взаимную индуктивность M (величину и знак) двумя способами:
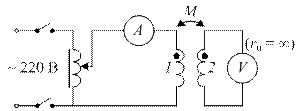
а) измерением ЭДС взаимной индукции при синусоидальном токе и определением полярности ЭДС взаимной индукции при подключении на постоянное напряжение (рис. 16);
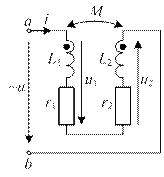
б) измерением эквивалентных индуктивностей при согласном и встречном последовательном включении катушек (схемы включения катушек показаны на рис. 17, измерительная схема та же, что и на рис. 14 в п. 2).
| 
|
| Рис. 15. Схема для определения абсолютной величины M | Рис. 16. Схема для определения знака M |
| 
|
| а) | б) |
| Рис. 17. Последовательное согласное (а) и встречное (б) соединение двух индуктивно связанных катушек. |
4. Используя экспериментально найденные параметры r 1, L 1, r 2 L 2, M рассчитать и построить векторные диаграммы напряжений для согласного и встречного последовательного соединения катушек. Величину тока при расчете взять такой же, как в опыте п. 3,б.
5. Исследовать зависимость эквивалентных параметров r э, L э относительно входных зажимов для цепи с магнитной связью (рис. 18) от величины активного сопротивления вторичной цепи R 2 (измерительная схема та же, что и на рис. 14 п. 2).
|
|
6. По параметрам r 1, L 1, L 2, M рассчитать зависимость эквивалентных параметров r э, L э от величины в схеме (рис. 18). Построить теоретические графики зависимостей r э(R 2) и L э(R 2) и нанести на них экспериментально снятые в п. 5 программы точки (см. пояснения).
|
| Рис. 18. Магнитная (трансформаторная) связь двух катушек. |
Методические указания
К пункту 2. Измерение параметров r, x при синусоидальном токе осуществляется обычно с помощью вольтметра, амперметра и ваттметра. Используются следующие формулы:
;;
или;;;.
Здесь U, I – действующие значения напряжения и тока; P – активная мощность. Индуктивность катушки
Измерительная часть (до зажимов a – b) схемы (рис. 14) используется при измерениях на переменном токе для всех пунктов программы, поэтому ее не следует разбирать: к зажимам a – b подключаются поочередно разные схемы. Исключением составляет схема из п. 3, а для определения знака M в целях экономии времени рекомендуется этот опыт выполнить последним.
К пункту 3,а. Величину взаимной индуктивности M при синусоидальном токе определяют по току в одной катушке и напряжению, индуцированному на зажимах другой катушки (см. схему на рис. 15)
Знак M при произвольной маркировке зажимов определяется с помощью схемы (рис. 16). Здесь используется магнитоэлектрический вольтметр, реагирующий на знак измерительного напряжения. При указанном на схеме согласовании полярностей источника, вольтметра и маркировки зажимов взаимная индуктивность M будет положительным числом, если включение цепи приведет к положительному отклонению стрелки вольтметра, наоборот,, если отклонение отрицательно (см. пояснения).
|
|
К пункту 3,б. Термины «согласное включение» и «встречное включение» применяются для последовательного соединения катушек только при. Будем называть соединение на рис. 17,а «условно согласным», а на рис. 17,б – «условно встречным» включением, считая M алгебраическим числом, т.е. при произвольной маркировке. Эти термины указывают на совпадение или несовпадение ориентации стрелок тока в катушках относительно произвольно маркированных зажимов (см. пояснения). Измерив эквивалентные индуктивности L э.согл и L э.встр для обеих систем, можно определить величину и знак M по формуле:
так как, а.
Опыты по определению эквивалентных индуктивностей L э.согл и L э.встр производятся так же, как и для одиночной катушки (п. 2). Рекомендуется опыты производить при одном и том же значении тока – это облегчит сравнение векторных диаграмм (п. 5 программы).
К пункту 4. Схема опыта к п. 4 программы (рис. 18), представляет по существу воздушный трансформатор, включенный на активную нагрузку (тарированный реостат r). Результирующее активное сопротивление вторичной цепи, где r 2 – собственное сопротивление второй катушки. Измерения рекомендуется выполнить для 4 – 5 значений r, включая предельные (закоротка) и (разрыв).
Пояснения к работе
При математическом описании электромагнитного процесса в индуктивной катушке, обладающей активным сопротивлением r и индуктивностью L, необходимо задать условные положительные направления (стрелками) тока i, напряжения на зажимах u (всегда вычисляемого по внешнему пути), потокосцепления самоиндукции YL и индуцированной ЭДС.
|
|
|
| Рис. 19. Система стрелок для i, e L, YL, u одиночной катушки. |
Наиболее распространенная система стрелок показана на рис. 19. Здесь i и e L вычисляются в направлении обхода контура, а YL – в направлении положительной нормали («правый винт»), направления стрелок напряжения u и тока i одинаково по отношению к внешним зажимам. Формулы для системы стрелок (рис. 19) таковы:
;
при,.
Если по каким-либо соображениям стрелка одной из величин выбрана в противоположном направлении, то во всех приведенных формулах, куда входит указанная величина, следует ее знак изменить на противоположный. Например, иногда ЭДС самоиндукции вычисляют в направлении, противоположном току (такую ЭДС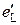 
называют «противо-ЭДС»), при этом 
.
При описании совокупности катушек с общим магнитным полем наиболее универсальной системой стрелок является система, использующая произвольную маркировку катушек, когда взаимную индуктивность M считают алгебраической величиной.
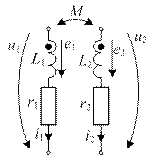
На рис. 20 изображены две индуктивно связанные катушки (контуры). Один из пары зажимов каждой катушки маркирован – отмечен точкой (·). Тем самым задают систему отсчета (т.е. стрелками) токов, потоков, ЭДС и напряжений на зажимах обеих катушек.
| 
|
| а) | б) |
| Рис. 20. Система стрелок для двух индуктивно связанных катушек, а) пространственное изображение индуктивно связанных катушек; б) эквивалентная схема замещения индуктивно связанных катушек. |
Системы отсчета «обход – нормаль» для индуктивно связанных катушек совершенно аналогичны системе, принятой на рис. 19 для одиночной катушки. Только на рис. 20 Y1 и Y2 – это результирующие потокосцепления.
| ; . | (1) |
Напряжения u 1 и u 2 на зажимах катушек при L 1, L 2, M – const.
| ; . | (2) |
Индуктируемые ЭДС
| ; . | (3) |
Вычисление собственного и взаимного потокосцеплений в катушке производится в одну и ту же сторону (стрелка нормали), поэтому в уравнениях (1) слагаемые суммируются.
Одинаковым образом вычисляются также ЭДС само- и взаимной индукции (стрелка обхода) для каждой катушки, поэтому и в формулах (2) соответствующие слагаемые суммируются.
В случае произвольного количества индуктивно связанных катушек уравнения для Yk, e k, u k любой k -й катушки имеют структуру, аналогичную (1), (2), (3) только с большим числом членов, учитывающих индуктивные связи данной катушки с остальными.
В уравнениях (1), (2), (3) взаимная индуктивность считается алгебраическим числом. Для выбранной маркировки пары катушек 1 и 2 M положительно, если при положительных токах i 1 и i 2 результирующие потокосцепления Y1 и Y2 больше потокосцеплений самоиндукции и («Взаимоиндукция усиливает поле»); M – отрицательно, если при положительных токах i 1 и i 2 «взаимоиндукция ослабляет поле». Отметим, что знак M жестко связан с маркировкой: если перенести маркировку в катушке с одного зажима на другой, то знак M меняется на противоположный. Поэтому нельзя говорить о знаке M, не указывая, для каких маркированных зажимов определялся параметр M.
На практике принять называть «одноименными зажимами» двух катушек такую пару маркированных зажимов, которым соответствует. Если считать M алгебраической величиной, то произвольно маркированные зажимы можно называть «условно одноименными». Поэтому при экспериментальном определении M для пары катушек поступают так. Вначале маркируют зажимы произвольно и определяют знак M. Если окажется, что, перемаркируют одну из катушек, чтобы сделать M положительным. Однако, в случае, когда имеется несколько катушек, сделать все M km положительными бывает невозможно, тогда оставляют маркировку с «условно одноименными зажимами», указывая величину и знак M km для каждой пары катушек k и m.
Уравнения (1), (2), (3) соответствуют направлению стрелок i, Y, e, u на рис. 20. Но в схемах направление некоторых стрелок по отношению к маркированным зажимам может отличаться. Для правильности составления уравнений в этих случаях руководствуются следующим: если направление стрелки какой-либо величины изменить на противоположное, то знак во всех членах формул (1), (2), (3), куда входит эта величина, нужно изменить на противоположный. Например, пусть на рис. 20 стрелку i 2 изменили на противоположную, т.е. ввели ток 
. Тогда из (1), (2), (3) для одной катушки получим:
;
;
.
Ориентацию токов i 1 и i 2 (рис. 20) по отношению к маркированным зажимам будем называть согласной, а ориентацию i 1 и 
встречной.
Применим изложенные выше положения к исследуемым цепям.
1. Объяснить правило, по которому определяется знак M в схеме на рис. 16 (включение на постоянное напряжение).
На данной схеме ориентация стрелок токов и напряжений по отношению к маркированным зажимам соответствует схеме (рис. 20) и формулам (1) – (3). Напряжение на вольтметре
,
Так как вследствие большого сопротивления прибора. При включении цепи ток i 1 возрастает, т.е.. Поэтому при положительном отклонении стрелки вольтметра () знак M – положительный, а при будет.
2. Найти теоретически зависимость эквивалентных параметров r э, x э от величины R 2 (схема на рис. 18).
Схеме на рис. 18 соответствует комплексная схема (рис. 21).
Здесь;
;
Ориентация стрелок 
и 
по отношению к маркированным зажимам – согласная.
Расчетные уравнения в комплексной форме, соответствующие формулам (3):
;
;
откуда
.
Эквивалентное (входное) сопротивление цепи Z э равно:
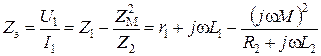
После преобразований получим
На рис. 22 приведен вид графиков r э(R 2) и x э(R 2) при изменении.
При,
При – вторичная цепь не имеет тепловых потерь.
– вторичная цепь оказывает наибольшее размагничивающее действие. Последнюю формулу часто записывают в виде,
где - коэффициент магнитной связи.
В теории доказывается, что всегда. При имеет место максимум r э (доказать самостоятельно).
| 
| |
| Рис. 21. Расчетная схема воздушного трансформатора | Рис. 22. Зависимость эквивалентных (входных) сопротивлений r э и x э воздушного трансформатора от величины активного сопротивления вторичной цепи R 2 |
Выполняя опыт п. 6 программы, следует рассчитать r э и x э для значений R 2, равных 0; 0,5 x 2; x 2; 2 x 2; ∞. Теоретические графики нужно для сравнения совместить с экспериментальными. Заметим, что в опыте осуществить нельзя, так как R 2мин равно активному сопротивлению обмотки второй катушки r 2.
Контрольные вопросы
1. Дайте определение параметрам r и L катушки. Поясните физический смысл этих параметров. Нарисуйте схему и напишите формулы, по которым определяются r и L опытным путем при синусоидальном режиме.
2. Дайте определение и поясните физический смысл параметра M для пары катушек (контуров). Покажите систему отсчета для I и Y при произвольной маркировке катушек.
3. Напишите выражения для индуктированных ЭДС напряжений на зажимах каждой из двух индуктивно связанных катушек. Как маркировка влияет на знаки в этих выражениях?
4. Перечислите и объясните все опыты, производимые в данной работе по определению величины и знака M. Какие способы вам еще знакомы?
5. Выведите зависимости r э, x э, z э от величины активного сопротивления R 2 вторичной цепи для схемы (рис. 18).
6. Объясните графики зависимостей r э(R 2) и x э(R 2). Почему всегда, а?
ЛАБОРАТОРНАЯ РАБОТА №11