Лекция 4.
(с.)
МАТЕМАТИЧЕСКИЕ МОДЕЛИ И СТРУКТУРНЫЕ СХЕМЫРЕГУЛЯТОРОВ
ВЛИЯНИЕ МЕСТНЫХ ОС
Основные виды ОС определяются ПФ (рис. 1.22):
• жесткая обратная связь (действует на систему как в переходном, так и установившемся режимах)

• инерционная жесткая ОС

• гибкая обратная связь (действует лишь в переходных режимах)

• инерционная гибкая ОС
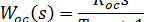

|
 (t)
(t) 
-

|
Рис. 1.22. Структурная схема системы с обратной связью W oc(s)
Проиллюстрируем основные свойства ОС при охвате ими различных
типов звеньев.
Пусть
 тогда
тогда

Где

Вывод: жесткая отрицательная ОС не меняет структуру апериодического звена, но уменьшает его инерционность (уменьшает постоянную времени).
Тем самым она улучшает качество переходного процесса в САУ и оказывает
стабилизирующее действие, т.е. превращает неустойчивую замкнутую систему в
устойчивую.
Если же


То

Где

Таким образом, гибкая отрицательная ОС не изменяет структуру и не влияет на передаточный коэффициент апериодического звена. Она лииіь увеличивает его инерционность (увеличивает его постоянную времени). Положим теперь, что

а

В этом случае получаем

Где

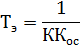
Итак, под действием жесткой ОС теряется интегрирующее свойство звена и оно превращается в апериодическое с коэффициентом усиления, который определяется  . Постоянная времени
. Постоянная времени  будет мала при большом К.
будет мала при большом К.
1 случай. Рассмотрим случай, когда


Имеем

где

Следовательно, интегрирующее звено превращается в звено второго порядка; при большом К охват интегрирующего звена инерционной жесткой обратной
связью эквивалентен усилительному звену с введением производной.
2 случай. Если же


Где
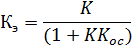
Таким образом, гибкая обратная связь не изменяет структуру интегрирующего звеңц, но умеңьшает его передаточный коэффициент (увеличивает постоянную времеңи  ).
).
3 случай. Рассмотрим практически важный случай, когда

Передаточная функция замкнутой системы имеет вид

где

Вывод: жесткая отрицательная ОС не изменяет структуру колебательного звена, но уменьшает постоянную времени и коэффициент демпфирования. при этом уменьшается коэффициент передачи
4 случай. Если же колебательное звено охватывается отрицательной ОС с ПФ

то при


где
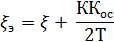
Если же

то

где
 ;
;  ;
;  .
.
Следовательно, сильная отрицательная ОС превращает колебательное звено в последовательное соединение двух апериодических звеньев
5 случай. Легко показать, что если


где

т.е. инерционная отрицательная ОС превращает идеальное усилительное звено в реальное дифференцирующее звено, с помощью которого можно получить производ- ные входного сигнала.
Последовательный регулятор, имеющий ПФ

и объединяющий в себе введение интеграла и производной, называется изодромным. Использование изодромного регулятора позволяет получить необходимый порядок астатизма, сохраняя устойчивость и качество системы в переходном режиме.
6 случай. А теперь рассмотрим случай, когда объект с ПФ

охватывается ОС с ПФ

Пользуясь структурными преобразованиями, получим ПФ замкнутой системы

где

Вывод: при сохранении интегрирующего свойства звена получается эффект
введения производной, т.е. интегрирующее звено становится изодромным (постоянные времени Т1 и Т2 могут быть уменьшены за счет увеличения К). Инерционное запаздывание в ОС может быть использовано для улучшения качества переходных процессов (получается эффект, аналогичный введению производной в прямой цепи).
В заключение рассмотрим условие сохранения порядка астатизма
охватываемого звена.
Если
 то
то

Отсюда следует, что для сохранения v-го порядка астатизма необходимо выполение условия µ ≥ v.
Общий вывод: применение даже простейших отрицательных обратных связей позволяет существенно изменять свойства типовых звеньев. Если же элементы регулятора могут быть охвачены ОС, то динамические свойства этих элементов могут быть изменены в направлении обеспечения заданного качества работы
замкнутой САУ.
Изложенные здесь положения лежат в основе подходов к выбору рациональной структуры регулятора для каждого конкретного случая. При проведении инженер-ных расчетов целесообразно принимать во внимание следующее. Уменьшение уста-новившейся ошибки достигается увеличением добротности системы (передаточного коэффициента разомкнутой системы). Вместе с тем при увеличении коэффициента усиления в большинстве случаев уменьшаются запасы устойчивости и при К >Ккр система становится неустойчивой. Поэтому при повышении точности работы САУ
в установившемся режиме путем увеличения К необходимо предусмотреть мероприятия для обеспечения достаточного запаса устойчивости. Увеличение точности путем обеспечения астатизма (включение интеграторов в прямую цепь) также требует реализации мероприятий по сохранению запасов устойчивости САУ. Для получения астатизма целесообразно использовать изодромные звенья с ПФ

где
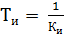 постоянная времени изодрома.
постоянная времени изодрома.
Если Ти - достаточна велика, то запас устойчивости может быть сохранен неиз- менным [130]. Неединичная обратная связь - один из путей реализации астатической системы. Демпфирование с подавлением высоких частот - еще один путь обеспечения ус- тойчивости или повышения запаса устойчивости. Этот путь реализуется введением апериодического звена, постоянная времени которого значительно больше постоян- ных времени имеющихся апериодических звеньев разомкнутой системы
 .
.
Устойчивость и необходимый запас устойчивости могут быть обеспечены вве- дением форсирующего звена при любой ПФ исходной системы. При этом увеличива- ется быстродействие системы, вместе с тем увеличивается и влияние помех.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ И СТРУКТУРНЫЕ СХЕМЫРЕГУЛЯТОРОВ
В предыдущем параграфе была показана роль операций усиления, интегрирова- ния и дифференцирования: с помощью изменения величины коэффициента усиления в прямой цепи, введения местных обратных связей, включения интегрирующих и дифференцирующих звеньев можно добиться заданного качества работы САУ (в пределах возможностей, которые определены структурой используемого регулятора). В соответствии с этим положением строятся математические модели регуляторов, цель которых - формирование управляющего воздействия (команды управления) на объект.

|
 (t)
(t) 
-

|
Рис. 1.22. Структурная схема системы с обратной связью W oc(s)
Здесь пока ограничимся рассмотрением наиболее распространенных математических моделей линейных регуляторов по отклонению непрерывного действия. В этих простейших законах управляющее воздействие u(t) линейно зависит от сигнала ошибки  (включение в прямую цепь усилителя), его интеграла (включение интегрирующих звеньев) и первой производной (включение дифференцирующих звеньев). Сказанное выше позволяет ввести в рассмотрение следующие виды управляющих устройств (регуляторов):
(включение в прямую цепь усилителя), его интеграла (включение интегрирующих звеньев) и первой производной (включение дифференцирующих звеньев). Сказанное выше позволяет ввести в рассмотрение следующие виды управляющих устройств (регуляторов):
1) пропорциональное управляющее устройство (П-управление)

2) интегральное управляющее устройство (И-управление)
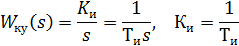
3) пропорционально-интегральное управляющее устройство (ПИ-управление)

4) пропорционально-дифференциальное управляющее устройство (ПД-управление)

5) пропорционально-интегрально-дифференциальное управляющее устройство (ПИД-управление)
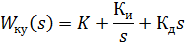
Вводя кратное интегрирование и дифференцирование, можно получить более сложные законы управления.