ЭЛЕМЕНТЫ ЦЕНТРАЛЬНОЙ ПРОЕКЦИИ

Задание 1.

Цель занятия - изучение геометрических свойств изображений, построенных по законам центральной проекции.

Задачи работы:

· изучить элементы центральной проекции;

· изучить способы построения перспектив точек и прямых;

· построить на пространственных чертежах, по основные элементы центральной проекции;

· построить перспективы точек, перспективу отрезка прямой и перспективу отрезка отвесной прямой.

Содержание занятия. Выбрать индивидуальные исходные данные, познакомиться со способами построения изображения на аэрофотоснимках, изучить термины и определения, построить основные элементы центральной проекции на пространственном чертеже, выполнить построение перспективы точек и отрезков прямых, ответить на контрольные вопросы.

Литература [1, 2].

Теоретические пояснения к занятию

Для решения многих задач, особенно в инженерном деле, широко ис­пользуют изо­бра­жения объектов, построенные тем или иным мето­дом на плоскости или на поверхности.

Построение изображения какого-либо предмета (объекта) на из­бран­ной поверхности по определенному закону называется проекти­рова­нием, а его результат – проекцией.

При аэрофотосъемке изображение на снимке получается путем центрального проектирования точек местности на фотопленку, расположенную в фокальной плоскости аэрокамеры. При этом узловая точка объектива играет роль центра проектирования S, плоскость фотопленки (аэрофотоснимок) – картинной плоскости Р, а плоскость, где размещаются объекты съемки, - предметной Е. Параметрами полученного таким образом снимка являются угол наклона α_с плоскости снимка (картинной плоскости) по отношению к предметной, высота фотографирования Н над этой плоскостью и фокусное расстояние f (удаление узловой точки объектива или центра проектирования от плоскости снимка).

В связи с этими исходными данными для построения элементов центральной проекции являются указанные выше величины α_с, f и Н. Причем, f и Н не являются элементами центральной проекции, но они необходимы для нанесения на чертеж всех элементов.

Для построения элементов центральной проекции необходимо иметь три основных элемента: центр проекции S, предметную плоскость Е, где размещены объекты, картинную плоскость Р, где получаются изображения этих объектов. Остальные элементы получаются как следы сечения основных плоскостей Р и Е с лучами и плоскостями, проведенными по определенным правилам.

Исходные данные для выполнения лабораторной работы представлены в приложении 1.

Практические пояснения к занятию

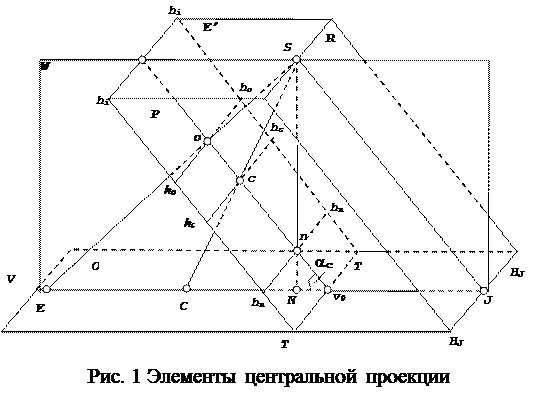
Задание 1. Основные элементы центральной проекции (чертеж формата А3).

Основание картины ТТ ( рис.1) получается как след сечения картинной и предметной плоскостей. Плоскость главного вертикала (W) проходит через центр проекции перпендикулярно основанию картины; точка ее пересечения (υ_о) с основанием картины (ТТ) называется главной точкой основания картины, а след сечения с картиной (i υ_о) и предметной (υ_оV) плоскостями – главной вертикалью и ее проекцией соответственно. Угол α_c, образованный предметной и картинной плоскостями называется суммарным углом наклона картинной плоскости. Опустив перпендикуляр из S на главную вертикаль получим главную точку картины (о) и ее проекцию (О). Опустив перпендикуляр из S на проекцию главной вертикали v₀V получимпроекцию (N) точки надира (n). Точка надира образуется на пересечении данного перпендикуляра с главной вертикалью (υ₀ i). Биссектриса угла oSN пересечет картинную и предметную плоскости в точке нулевых искажений (с) и ее проекции (С) соответственно. Плоскость действительного горизонта Е′, пройдет через центр проекции S параллельно предметной плоскости. В сечении с плоскостью Р и главной вертикалью (υ₀ i) даст линию действительного горизонта (h_i h_i) и главную точку схода картинной плоскости (i).Разделяющая (нейтральная) плоскость R, проведенная через центр проекции S параллельно картинной плоскости Р, даст в сечении с предметной плоскостью и проекцией главной вертикали соответственно линию картинного горизонта (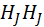) и точку схода предметной плоскости (J).

Любая прямая картинной плоскости, параллельная основанию картины (перпендикулярная главной вертикали) называется горизонталью. Горизонталь, проходящая через главную точку картины, называется главной (). Горизонталь, проходящая через точку нулевых искажений – линией неискаженных масштабов (h_с h_с), а горизонталь, проходящая через точку надира – надирной горизонталью (h _n h_n).

Построение указанных элементов выполняют в следующем порядке: отступив от нижнего края листа 7-9 см, проводят горизонтальную прямую и принимают ее за проекцию главной вертикали υ₀ V. На этой линии, на расстоянии 15-18 см от левого края листа выбирают точку N, из которой восстанавливают перпендикуляр и откладывают вдоль него отрезок, равный высоте фотографирования H, получают центр проекции S. 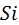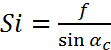Из центра проекции S проводят прямую, параллельную проекции главной вертикали и откладывают вдоль нее отрезок равный , который вычисляется по формуле (1):

(1).

Получают главную точку схода i. Из точки i под углом к отрезку Si проводят прямую 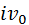, длина которой должна быть равной величине, вычисленной по формуле 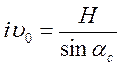(2):

(2).

В пересечении 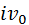и SN получают точку надира n. Из центра проекции опускают перпендикуляр на главную вертикаль 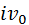(его длина равна f) и продолжают его до пересечения с 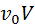, получают главную точку картины о и ее проекцию О. Проведя биссектрису угла OSN в пересечении с главной вертикалью и ее проекцией получают точки с и С. Построив основные линии, оформляют плоскости, как показано на рис. 1. Длину основания картины ТТ принимают равной 80 мм, а проекцию главной вертикали 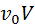- 200-250 мм.

Задание 2. Построение перспективы точек и отрезка прямой, лежащих в предметной плоскости (чертеж формат А4).

Изображение предмета, полученное в результате центрального проектирования, называется перспективой. Приступая к отысканию перспективы точек и прямых, следует иметь ввиду, что во всех случаях решение сводится к нанесению на плоскость Р следа сечения ее проектирующей плоскостью, проведенной через центр проекции S и заданную прямую.

В предметной плоскости Е по координатам Х и У наносят точки А и С. Оси координат совпадают с проекцией главной вертикали 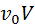и линией основания картины 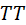(рис.2).

Из точек А и С опускают перпендикуляры на 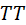(проводят линии параллельные проекции главной вертикали) получая двойные точк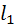и и 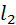. Из них проводят направления перспектив точек А и С – отрезки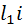 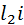. Для нахождения перспектив точек проводят проектирующие лучи SA и SC. Точки пересечения этих лучей с направлениям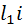и и 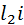и будут искомыми перспективами а и с, а отрезок ас – перспективой отрезка АС.

Данный метод нахождения перспектив называется методом перпендикуляров. Перспектива отрезка может быть также найдена методом направления перспективы. Для этого отрезок АС продолжают до пересечения с ТТ получая двойную точку 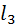. В плоскости действительного горизонта Е из центра проекции S проводят линию параллельную отрезку АС до пересечения с линией действительного горизонта 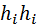. Точка пересечения является точкой схода прямой 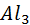, а перспектива отрезка АС будет находиться на направлении перспективы 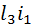. Для нахождения перспективы ac отрезка прямой AC достаточно провести в его концы из центра проекции S проектирующие лучи SA и SC, которые отсекут на направлении перспективы искомую проекцию.

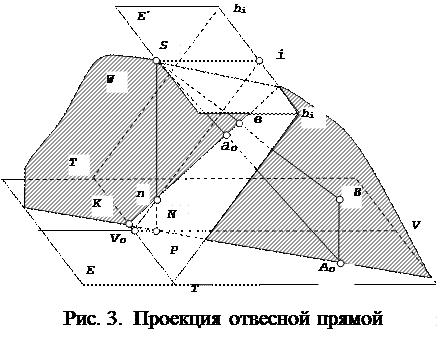
Задание 3. Построение перспективы отвесной прямой.

Задача построения перспективы отвесной прямой решается указанным выше способом, т.е. путем нанесения следов сечения предметной и картинной плоскостей проектирующей плоскостью. Особенностью решения является определение положения двойной точки, так как заданная прямая и основание картины не пересекаются при их продолжении.

В предметной плоскости Е по координатам наносят точку А. Так как точка В имеет такие же координаты Х и У, в точке А восстанавливают перпендикуляр к плоскости Е и откладывают вдоль него аппликату точки В.

Для определения положения линии пересечения предметной и проектирующей плоскости воспользуемся тем, что основание данной прямой А (рис.3) и проекция точки надира N принадлежат линии их пересечения. Тогда для определения положения двойной точки l необходимо соединить основание заданной прямой А с проекцией точки надира N и продолжить до пересечения с основанием картины ТТ. Направление перспективы, как указывалось ранее, проходит через двойную точку и точку схода, которая для отвесных прямых совпадает с точкой надира n.

Второй способ

Второй способ определения перспективы отвесной прямой предполагает использование вспомогательной плоскости, проходящей параллельно предметной через пространственную точку.

Для нанесения нового основания картины (линии пересечения картинной и вспомогательной плоскостей) от проекции точки надира вдоль луча NS откладывают аппликату пространственной точки, а из полученной точки N проводят прямую 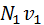перпендикулярную SN до пересечения с главной вертикалью. Горизонталь ТТ, проходящая через точку 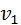, и будет основанием вспомогательной плоскости.

Поскольку пространственная точка В лежит в новой предметной плоскости Е, нахождение ее проекции выполняется методом перпендикуляров.

Для получения перспективы отвесной прямой ВА достаточно соединить проекции точек В и А в картинной плоскости P.

Контрольные вопросы

1. Дайте определение центральной проекции.

2. Назовите три основных элемента для построения пространственного чертежа элементов центральной проекции.

3. Назовите основные точки, линии и плоскости элементов центральной проекции.

4. Особенности построения перспективы точек и отрезков прямой, лежащих в предметной плоскости.

5. Особенности построения перспективы отрезка отвесной прямой.

Задание 2.