БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Механико–математический факультет
Кафедра общей математики и информатики
Матейко О. М., Плащинский П.В.
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ВЫСШАЯ МАТЕМАТИКА
Часть 2
МИНСК
Ó Матейко О. М., Плащинский П.В., 2005.
Интегральное исчисление функций
Одной переменной
Перечень вопросов по теме
1. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.
2. Таблица интегралов. Основные методы интегрирования: непосредственное интегрирование, метод подстановки, метод интегрирования по частям.
3. Интегрирование рациональных дробей с квадратным трехчленом в знаменателе.
4. Интегрирование иррациональных функций с квадратным трехчленом в знаменателе.
5. Интегрирование рациональных функций.
6. Интегрирование тригонометрических выражений.
7. Интегрирование иррациональных функций.
8. Определенный интеграл: определение, геометрический и физический смысл. Условия интегрируемости функций.
9. Свойства определенного интеграла. Теорема о среднем.
10. Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.
11. Замена переменной в определенном интеграле. Формула интегрирования по частям.
12. Приложения определенного интеграла: вычисление площадей плоских фигур, длины дуги плоской кривой, объемов геометрических тел.
Задание 1. Вычислить указанные неопределенные интегралы.
| 0. | 0.1. |  ; ;
| 0.2. |  ; ;
|
| 0.3. | 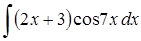 ; ;
| 0.4. |  ; ;
| |
| 0.5. |  ; ;
| 0.6. |  . .
|
Решение варианта 0.
Пример 0.1. Непосредственным интегрированием получаем:
 .
.
Пример 0.2. Аналогично,
 .
.
Пример 0.3. Применяя формулу интегрирования по частям, имеем:

 .
.
Пример 0.4. Применяя тригонометрические формулы понижения степени, приводим интегралы к табличному виду:



 .
.
Пример 0.5. Выделяем в числителе производную знаменателя, а затем, выделяя в трехчлене полный квадрат, приводим интегралы к табличному виду:



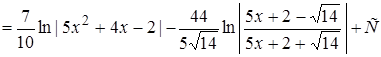 .
.
Пример 0.6. После степенной замены подынтегральная функция становится рациональной:





 .
.
| 1. | 1.1. |  ; ;
| 1.2. |  ; ;
|
| 1.3. |  ; ;
| 1.4. |  ; ;
| |
| 1.5. |  ; ;
| 1.6. |  . .
|
| 2. | 2.1. |  ; ;
| 2.2. |  ; ;
|
| 2.3. |  ; ;
| 2.4. |  ; ;
| |
| 2.5. |  ; ;
| 2.6. | 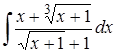 . .
|
| 3. | 3.1. |  ; ;
| 3.2. |  ; ;
|
| 3.3. |  ; ;
| 3.4. |  ; ;
| |
| 3.5. |  ; ;
| 3.6. | 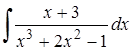 . .
|
| 4. | 4.1. | 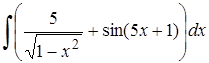 ; ;
| 4.2. |  ; ;
|
| 4.3. |  ; ;
| 4.4. | 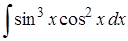 ; ;
| |
| 4.5. | 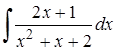 ; ;
| 4.6. |  . .
|
| 5. | 5.1. | 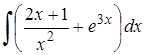 ; ;
| 5.2. |  ; ;
|
| 5.3. |  ; ;
| 5.4. |  ; ;
| |
| 5.5. |  ; ;
| 5.6. |  . .
|
| 6. | 6.1. |  ; ;
| 6.2. |  ; ;
|
| 6.3. |  ; ;
| 6.4. |  ; ;
| |
| 6.5. | 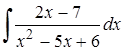 ; ;
| 6.6. |  . .
|
| 7. | 7.1. |  ; ;
| 7.2. |  ; ;
|
| 7.3. |  ; ;
| 7.4. |  ; ;
| |
| 7.5. |  ; ;
| 7.6. |  . .
|
| 8. | 8.1. |  ; ;
| 8.2. |  ; ;
|
| 8.3. |  ; ;
| 8.4. |  ; ;
| |
| 8.5. |  ; ;
| 8.6. |  . .
|
| 9. | 9.1. |  ; ;
| 9.2. |  ; ;
|
| 9.3. |  ; ;
| 9.4. |  ; ;
| |
| 9.5. | 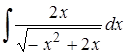
| 9.6. |  . .
|
| 10. | 10.1. |  ; ;
| 10.2. |  ; ;
|
| 10.3. |  ; ;
| 10.4. |  ; ;
| |
| 10.5. |  ; ;
| 10.6. |  . .
|
| 11. | 11.1. |  ; ;
| 11.2. |  ; ;
|
| 11.3. |  ; ;
| 11.4. |  ; ;
| |
| 11.5. |  ; ;
| 11.6. |  . .
|
| 12. | 12.1. |  ; ;
| 12.2. |  ; ;
|
| 12.3. |  ; ;
| 12.4. |  ; ;
| |
| 12.5. |  ; ;
| 12.6. |  . .
|
| 13. | 13.1. |  ; ;
| 13.2. |  ; ;
|
| 13.3. |  ; ;
| 13.4. | 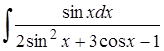
| |
| 13.5. |  ; ;
| 13.6. |  . .
|
| 14. | 14.1. |  ; ;
| 14.2. |  ; ;
|
| 14.3. |  ; ;
| 14.4. |  ; ;
| |
| 14.5. | 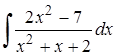 ; ;
| 14.6. |  . .
|
| 15. | 15.1. |  ; ;
| 15.2. | 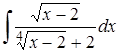 ; ;
|
| 15.3. |  ; ;
| 15.4. |  ; ;
| |
| 15.5. |  ; ;
| 15.6. |  . .
|
| 16. | 16.1. | 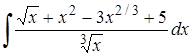 ; ;
| 16.2. | 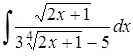 ; ;
|
| 16.3. |  ; ;
| 16.4. |  ; ;
| |
| 16.5. |  ; ;
| 16.6. |  . .
|
| 17. | 17.1. |  ; ;
| 17.2. | 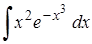 ; ;
|
| 17.3. |  ; ;
| 17.4. |  ; ;
| |
| 17.5. |  ; ;
| 17.6. |  . .
|
| 18. | 18.1. |  ; ;
| 18.2. | 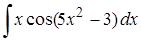 ; ;
|
| 18.3. |  ; ;
| 18.4. |  ; ;
| |
| 18.5. |  ; ;
| 18.6. |  . .
|
| 19. | 19.1. |  ; ;
| 19.2. |  ; ;
|
| 19.3. |  ; ;
| 19.4. |  ; ;
| |
| 19.5. |  ; ;
| 19.6. |  . .
|
| 20. | 20.1. | 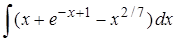 ; ;
| 20.2. |  ; ;
|
| 20.3. |  ; ;
| 20.4. |  ; ;
| |
| 20.5. |  ; ;
| 20.6. |  . .
|
| 21. | 21.1. |  ; ;
| 21.2. |  ; ;
|
| 21.3. |  ; ;
| 21.4. |  ; ;
| |
| 21.5. |  ; ;
| 21.6. |  . .
|
| 22. | 22.1. |  ; ;
| 22.2. |  ; ;
|
| 22.3. |  ; ;
| 22.4. |  ; ;
| |
| 22.5. |  ; ;
| 22.6. |  . .
|
| 23. | 23.1. |  ; ;
| 23.2. |  ; ;
|
| 23.3. |  ; ;
| 23.4. |  ; ;
| |
| 23.5. | 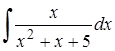 ; ;
| 23.6. |  . .
|
| 24. | 24.1. |  ; ;
| 24.2. |  ; ;
|
| 24.3. |  ; ;
| 24.4. |  ; ;
| |
| 24.5. |  ; ;
| 24.6. |  . .
|
| 25. | 25.1. | 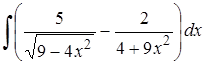 ; ;
| 25.2. |  ; ;
|
| 25.3. | 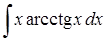 ; ;
| 25.4. |  ; ;
| |
| 25.5. |  ; ;
| 25.6. |  . .
|

 Задание 2. Вычислить следующие определенные интегралы:
Задание 2. Вычислить следующие определенные интегралы:
| 0. | 0.1. |  ; ;
| 0.2. |  ; ;
|
| 0.3. |  ; ;
| 0.4. |  . .
|
Решение варианта 0.
Пример 0.1. Применяя свойства определенного интеграла и формулу Ньютона-Лейбница, получаем:
 =
=  =
= 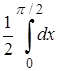 +
+ 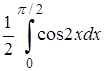 =
= 
 +
+
+ 
 =
=  .
.
Пример 0.2. Интегрируя по частям, находим
 =
=  =
= 
 –
–  =
=
=  –
–  =
=  –
–  =
=  –
– 
 +
+
+ 
 =
=  –
–  +
+  =
=  –
–  .
.
Пример 0.3. Введем новую переменную t по формуле  , тогда
, тогда  , 2 xdx = 2 tdt. Найдем новые пределы интегрирования: при x = 0имеем t = 1; при x =
, 2 xdx = 2 tdt. Найдем новые пределы интегрирования: при x = 0имеем t = 1; при x =  , t =2. Таким образом, получаем:
, t =2. Таким образом, получаем:
 =
=  =
=  = t
= t  = 2 – 1 = 1.
= 2 – 1 = 1.
Пример 0.4. Выделяя полный квадрат в знаменателе, получаем:
 =
=  =
=  =
=
= 
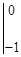 =
=  .
.
| 1. | 1.1. | 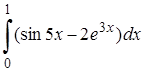 ; ;
| 1.2. | 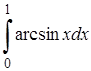 ; ;
|
| 1.3. |  ; ;
| 1.4. |  . .
|
| 2. | 2.1. |  ; ;
| 2.2. |  ; ;
|
| 2.3. |  ; ;
| 2.4. |  . .
|
| 3. | 3.1. | 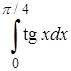 ; ;
| 3.2. |  ; ;
|
| 3.3. | 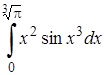 ; ;
| 3.4. |  . .
|
| 4. | 4.1. |  ; ;
| 4.2. |  ; ;
|
| 4.3. |  ; ;
| 4.4. |  . .
|
| 5. | 5.1. |  ; ;
| 5.2. |  ; ;
|
| 5.3. |  ; ;
| 5.4. | 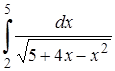 . .
|
| 6. | 6.1. |  ; ;
| 6.2. |  ; ;
|
| 6.3. |  ; ;
| 6.4. |  . .
|
| 7. | 7.1. | 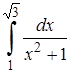 ; ;
| 7.2. |  ; ;
|
| 7.3. |  ; ;
| 7.4. |  . .
|
| 8. | 8.1. |  ; ;
| 8.2. | 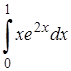 ; ;
|
| 8.3. |  ; ;
| 8.4. |  . .
|
| 9. | 9.1. |  ; ;
| 9.2. |  ; ;
|
| 9.3. |  ; ;
| 9.4. | 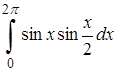 . .
|
| 10. | 10.1. |  ; ;
| 10.2. |  ; ;
|
| 10.3. |  ; ;
| 10.4. |  . .
|
| 11. | 11.1. | 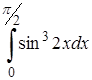 ; ;
| 11.2. |  ; ;
|
| 11.3. |  ; ;
| 11.4. |  . .
|
| 12. | 12.1. | 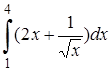 ; ;
| 12.2. |  ; ;
|
| 12.3. |  ; ;
| 12.4. |  . .
|
| 13. | 13.1. |  ; ;
| 13.2. |  ; ;
|
| 13.3. |  ; ;
| 13.4. |  . .
|
| 14. | 14.1. | 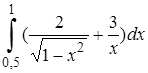 ; ;
| 14.2. |  ; ;
|
| 14.3. |  ; ;
| 14.4. |  . .
|
| 15. | 15.1. |  ; ;
| 15.2. |  ; ;
|
| 15.3. |  ; ;
| 15.4. |  . .
|
| 16. | 16.1. |  ; ;
| 16.2. |  ; ;
|
| 16.3. | 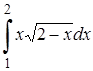 ; ;
| 16.4. | 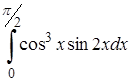 . .
|
| 17. | 17.1. |  ; ;
| 17.2. |  ; ;
|
| 17.3. |  ; ;
| 17.4. |  . .
|
| 18. | 18.1. |  ; ;
| 18.2. |  ; ;
|
| 18.3. |  ; ;
| 18.4. |  . .
|
| 19. | 19.1. |  ; ;
| 19.2. |  ; ;
|
| 19.3. |  ; ;
| 19.4. | 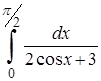 . .
|
| 20. | 20.1. |  ; ;
| 20.2. |  ; ;
|
| 20.3. |  ; ;
| 20.4. |  . .
|
| 21. | 21.1. | 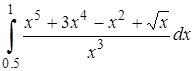 ; ;
| 21.2. |  ; ;
|
| 21.3. |  ; ;
| 21.4. |  . .
|
| 22. | 22.1. |  ; ;
| 22.2. |  ; ;
|
| 22.3. | 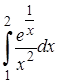 ; ;
| 22.4. |  . .
|
| 23. | 23.1. |  ; ;
| 23.2. |  ; ;
|
| 23.3. |  ; ;
| 23.4. |  . .
|
| 24. | 24.1. |  ; ;
| 24.2. |  ; ;
|
| 24.3. |  ; ;
| 24.4. |  . .
|
| 25. | 25.1. |  ; ;
| 25.2. |  ; ;
|
| 25.3. |  ; ;
| 25.4. |  . .
|
Задание 3. Вычислить площадь фигуры, ограниченной линиями.
0. y = x 2 – 2 x + 2, y = x + 2. 
Решение варианта 0.
 Данная фигура сверху ограничена прямой y = x + 2, снизу параболой y = x 2 – 2 x + 2. Искомую площадь вычислим по формуле S =
Данная фигура сверху ограничена прямой y = x + 2, снизу параболой y = x 2 – 2 x + 2. Искомую площадь вычислим по формуле S = 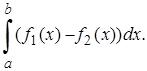 Пределами интегрирования будут абсциссы точек пересечения параболы и прямой. Решая систему уравнений y = x 2 – 2 x + 2, y = x + 2 находим:
Пределами интегрирования будут абсциссы точек пересечения параболы и прямой. Решая систему уравнений y = x 2 – 2 x + 2, y = x + 2 находим: 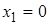 ,
,  , т. е. a = 0, b = 3. Таким образом получаем:
, т. е. a = 0, b = 3. Таким образом получаем:
S =  =
=  =
=
= 
 = –9 +
= –9 + 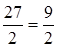
| 1. y = x + 1, y = cos x, y = 0. | 2. xy = – 2, y = x – 3. |
| 3. y = x 2, y = 3 – x. | 4. y = x 2 + 4 x, y = x + 4. |
5. y =  , y = x 3. , y = x 3.
| 6. y = – x 2 + 4, 2 x + y – 4 = 0. |
| 7. y = x – 2, y = x (2 – x). | 8. y = x 2 – 4 x, y = 0. |
| 9. y 2= 9 x, y = 3 x. | 10. y = – x 2 – 3 x + 6, y = x 2 – x – 6. |
| 11. y 2= 4 x, x 2= 4 y. | 12. x = y 2 – 6 y + 8, x + y = 4. |
| 13. y = x 2, y = 2 – x 2. | 14. y = – x 2 + 2 x – 1, y = – x + 1. |
15. y =  , y = , y =  . .
| 16. y =  , y = 0. , y = 0.
|
| 17. xy =5, x + y = 6. | 18. y = – x 2 + x + 3, y = x 2 – 5 x – 17. |
| 19. xy =4, x + y – 5 = 0. | 20. y = ln x, y = – x +1 + e, y = 0. |
21. y = x, y = 2 x, y =  . .
| 22. y = tg x, y = 2 x +1 –  , y = 0. , y = 0.
|
| 23. y 2= x + 1, y 2= 9 – x. | 24. y = tg x, y =  sin x. sin x.
|
| 25. y = x 2 + 2, x + y – 4 = 0. |
Задание 4. Вычислить объем тела, образованного вращением вокруг указанной оси фигуры, ограниченной линиями:
0. y = sin x, (0≤ x ≤p), y = 0, O x. 
Решение варианта 0.
Изобразим указанное тело на чертеже.

Искомый объем вычислим по формуле V =  . Имеем:
. Имеем:
V =  =
=  =
= 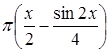
 =
=  .
.
| 1. y = 2 x – x 2, y = x, O x. | 2. y 2= 2 x, x = 4, y = 0, O x. |
3. y =  , y = x 2, O x. , y = x 2, O x.
| 4. y = ln x, (0≤ x ≤ a), y = 0, O x. |
| 5. y 2= x, x 2 = y, O x. | 6. y 2= 4 x, x = 2, y = 0, O x. |
| 7. y 2= 4 – x, x = 0, O y. | 8. xy =4, 2 x + y – 6 = 0, O x. |
9. y =  , (1≤ x ≤2), y = 0, O x. , (1≤ x ≤2), y = 0, O x.
| 10. y = 2 –  , x + y = 2, O y. , x + y = 2, O y.
|
| 11. y = – x 2 + 8, y = x 2, O x. | 12. y =  , y = x, O x. , y = x, O x.
|
| 13. y = x 3, x = 0, y = 8, O y. | 14. y = 4 – x 2, x ≥ 0, y = 0, O y. |
| 15. y = x – x 2, y = 0, O x. | 16. y = x 2 – 3 x + 2, y = 0, O x. |
| 17. y = x 2, y 2= 8 x, O y. | 18. y = sin x, (0≤ x ≤p), y = 1, O x. |
19. y =  ,(0≤ x ≤4), y = 0, O x. ,(0≤ x ≤4), y = 0, O x.
| 20. y = 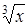 , y = x, O x. , y = x, O x.
|
21.  O y. O y.
| 22. y = tg x, (0≤ x ≤  ), y = 0, O x. ), y = 0, O x.
|
| 23.2 y 2 = x 3, y = 0, x = 4, O x. | 24. y 3 = 4 x 2, x = 0, y = 2, O y. |
| 25. x 2 + y 4 = y 2, O y. |