| 0. | 0.1. |  – 8 – 8  + 25 y = 0; + 25 y = 0;
| 0.2. |  – 7 – 7  + 12 y = – 48 s in3 x. + 12 y = – 48 s in3 x.
|
Решение варианта 0.
Пример 0.1. Характеристическое уравнение  имеет комплексные корни:
имеет комплексные корни:  , поэтому общее решение имеет вид: y =
, поэтому общее решение имеет вид: y =  (C 1 cos 3 x + C 2 sin 3 x).
(C 1 cos 3 x + C 2 sin 3 x).
Пример 0.2. Найдем общее решение соответствующего однородного уравнения  – 7
– 7  + 12 y = 0.. Характеристическое уравнение
+ 12 y = 0.. Характеристическое уравнение 
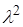 – –
– –  + 12 = 0 имеет различные действительные корни:
+ 12 = 0 имеет различные действительные корни:  , поэтому общее решение однородного уравнения определяется формулой
, поэтому общее решение однородного уравнения определяется формулой  . Частное исходного уравнения будем искать в виде y 1 = Acos 3 x + Bsin 3 x. Подставим y 1,
. Частное исходного уравнения будем искать в виде y 1 = Acos 3 x + Bsin 3 x. Подставим y 1,  = –3 Asin 3 x + 3 Bcos 3 x,
= –3 Asin 3 x + 3 Bcos 3 x, 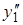 = = –9Acos 3 x – 9 Bsin 3 x в уравнение и получим:
= = –9Acos 3 x – 9 Bsin 3 x в уравнение и получим:
–9 Acos 3 x – 9 Bsin 3 x – 7(–3 Asin 3 x + 3 Bcos 3 x) +
+12(Acos 3 x + Bsin 3 x) = – 48 s in3 x,
или
(3 A – 21 B) cos 3 x + (21 A + 3 B) sin 3 x = – 48 s in3 x.
Последнее равенство должно выполнятся для всех x, и это возможно, когда 3 A – 21 B = 0, 21 A + 3 B = –48, A = – 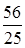 , B =
, B =  . Следовательно, y 1 = –
. Следовательно, y 1 = – 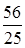 cos 3 x +
cos 3 x +  sin 3 x. Искомое общее решение неоднородного уравнения имеет вид: y =
sin 3 x. Искомое общее решение неоднородного уравнения имеет вид: y =  –
–  (7 cos 3 x + sin 3 x).
(7 cos 3 x + sin 3 x).
| 1. | 1.1. |  – –  – y = 0; – y = 0;
| 1.2. |  – 5 – 5  + 6 y = x 2 – x. + 6 y = x 2 – x.
|
| 2. | 2.1. |  – 2 – 2  + y = 0; + y = 0;
| 2.2. |  + +  + y = 3sin2 x. + y = 3sin2 x.
|
| 3. | 3.1. |  + 3 + 3  – 8 y = 0; – 8 y = 0;
| 3.2. |  – –  = x + 1. = x + 1.
|
| 4. | 4.1. |  – 4 – 4  + 5 y = 0; + 5 y = 0;
| 4.2. |  + 3 + 3  + 2 y = 5 e 5 x . + 2 y = 5 e 5 x .
|
| 5. | 5.1. |  – 2 – 2  + 5 y = 0; + 5 y = 0;
| 5.2. |  + +  – 2 y = cos x – 3sin x. – 2 y = cos x – 3sin x.
|
| 6. | 6.1. | 4  + 4 + 4  + y = 0; + y = 0;
| 6.2. |  – 2 – 2  + 10 y = 10 x 2 + 8 x + 6. + 10 y = 10 x 2 + 8 x + 6.
|
| 7. | 7.1. | 9  – –  – 2 y = 0; – 2 y = 0;
| 7.2. |  – 6 – 6  + 25 y = 3cos x + 2sin x. + 25 y = 3cos x + 2sin x.
|
| 8. | 8.1. |  + 3 + 3  = 0; = 0;
| 8.2. |  – 5 – 5  = sin5 x. = sin5 x.
|
| 9. | 9.1. |  – –  + 6 y = 0; + 6 y = 0;
| 9.2. |  + 2 + 2  + y = cos x + sin x. + y = cos x + sin x.
|
| 10. | 10.1. |  – 5 – 5  + 6 y = 0; + 6 y = 0;
| 10.2. |  – 7 – 7  + 12 y = e 3 x . + 12 y = e 3 x .
|
| 11. | 11.1. |  + 2 + 2  + y = 0; + y = 0;
| 11.2. |  + 2 + 2  + y = 4 x 2 – 3 x – 5. + y = 4 x 2 – 3 x – 5.
|
| 12. | 12.1. |  – 8 – 8  + 12 y = 0; + 12 y = 0;
| 12.2. |  + y = – sin2 x. + y = – sin2 x.
|
| 13. | 13.1. |  + +  – 6 y = 0; – 6 y = 0;
| 13.2. |  – –  – 2 y = 4 e 3 x . – 2 y = 4 e 3 x .
|
| 14. | 14.1. |  – 6 – 6  + 9 y = 0; + 9 y = 0;
| 14.2. |  + 2 + 2  = 4 x 3 – 2 x. = 4 x 3 – 2 x.
|
| 15. | 15.1. |  + 4 + 4  = 0; = 0;
| 15.2. |  + 4 + 4  + 4 y = 3cos2 x+ 2sin2 x. + 4 y = 3cos2 x+ 2sin2 x.
|
| 16. | 16.1. |  – 3 – 3  + 2 y = 0; + 2 y = 0;
| 16.2. |  – 4 – 4  + 4 y = e 2 x . + 4 y = e 2 x .
|
| 17. | 17.1. | 9  + y = 0; + y = 0;
| 17.2. |  + 2 + 2  + y = cos x + sin x. + y = cos x + sin x.
|
| 18. | 18.1. |  – y = 0; – y = 0;
| 18.2. |  – 4 – 4  + 3 y = 3 ex. + 3 y = 3 ex.
|
| 19. | 19.1. | 2  – 2 – 2  + 3 y = 0; + 3 y = 0;
| 19.2. |  – 6 – 6  + 9 y = 5sin x. + 9 y = 5sin x.
|
| 20. | 20.1. |  + 7 + 7  + 6 y = 0; + 6 y = 0;
| 20.2. |  –3 –3  + 2 y = ex. + 2 y = ex.
|
| 21. | 21.1. |  – 2 – 2  + 19 y = 0; + 19 y = 0;
| 21.2. |  + 2 + 2  + 2 y= 2 x 3 – 2. + 2 y= 2 x 3 – 2.
|
| 22. | 22.1. |  + +  – 12 y = 0; – 12 y = 0;
| 22.2. |  + 4 + 4  + 5 y = 5x 2 – 32 x + 5. + 5 y = 5x 2 – 32 x + 5.
|
| 23. | 23.1. | 2  – 3 – 3  – 2 y = 0; – 2 y = 0;
| 23.2. |  – 2 – 2  = x 2 – x. = x 2 – x.
|
| 24. | 24.1. |  – 4 – 4  + 7 y = 0; + 7 y = 0;
| 24.2. |  – 3 – 3  – 10 y = 3cos x + sin x. – 10 y = 3cos x + sin x.
|
| 25. | 25.1. |  + 4 + 4  – 7 y = 0; – 7 y = 0;
| 25.2. |  – 4 – 4  +3 y= 2 x + 1. +3 y= 2 x + 1.
|
Задание 13. Используя дифференциальные уравнения, решить следующие задачи.
Найти семейство функций, таких, что абсцисса точки пересечения касательной к графику каждой из них (в произвольной точке области определения функции) с осью абсцисс равна удвоенной абсциссе точки касания.
Решение варианта 0.
Выберем произвольную функцию искомого семейства и обозначим ее аргумент буквой x, а саму функцию y (x). Пусть (x 0, y 0) – произвольная точка графика этой функции. Уравнение касательной к графику функции в указанной точке будет иметь вид: y – y 0 = k (x – x 0), где k =  (x 0). Найдем абсциссу точки пересечения касательной с осью абсцисс. Для этого положим в уравнении касательной y = 0 и найдем значение переменной x из полученного уравнения. Легко видеть, что x =
(x 0). Найдем абсциссу точки пересечения касательной с осью абсцисс. Для этого положим в уравнении касательной y = 0 и найдем значение переменной x из полученного уравнения. Легко видеть, что x =  . По условию задачи имеем x = 2 x 0, и поэтому 2 x 0 =
. По условию задачи имеем x = 2 x 0, и поэтому 2 x 0 =  , или kx 0 = = – y 0. Опуская в этом уравнении индекс нуль и заменяя величину k ее значением, получим дифференциальное уравнение искомого семейства функций: x
, или kx 0 = = – y 0. Опуская в этом уравнении индекс нуль и заменяя величину k ее значением, получим дифференциальное уравнение искомого семейства функций: x  = – y. Это уравнение является уравнением с разделяющимися переменными. Разделяя переменные, получим:
= – y. Это уравнение является уравнением с разделяющимися переменными. Разделяя переменные, получим:  , откуда интегрированием находим, что ln6 y 6 = – ln6 x 6 + ln6 C 6. Значит, искомое семейство функций
, откуда интегрированием находим, что ln6 y 6 = – ln6 x 6 + ln6 C 6. Значит, искомое семейство функций 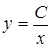 .
.
1. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат.
2. Найти кривую, проходящую через точку (0,2), касательные к которой отсекают от оси абсцисс отрезки в два раза большие ординаты точки касания.
3. Найти линии, у которых расстояние любой касательной от начала координат равно абсциссе точки касания.
4. Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания.
5. Угловой коэффициент касательной к кривой равен ординате точки касания. Найти уравнение кривой, проходящей через точку (0,3).
6. Найти линию, проходящую через точку (1,0) и обладающую тем свойством, что ордината точки пересечения касательной с осью ординат равна удвоенной сумме координат точки касания.
7. Найти кривые, для которых площадь треугольника образованного касательной, прямой, проходящей через точку касания перпендикулярно оси абсцисс и осью абсцисс, есть величина постоянная.
8. Найти кривую, у которой отрезок нормали в любой точке кривой, заключенной между осями координат, делится пополам в этой точке.
9. Найти уравнение кривой, проходящей через точку (3,1), для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
10. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу вдвое меньше абсциссы точки касания.
11. Определить и построить кривую, проходящую через точку (–2,2), если отрезок AB любой касательной к ней, заключенной между осями координат, делится точкой касания пополам.
12. Определить кривую, проходящую через точку (–1,1), если угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.
13. Найти уравнение кривой, проходящей через точку (4,3) и обладающую тем свойством, что длина отрезка нормали от точки кривой до точки пересечения с осью ординат равна 5.
14. Найти линию, проходящую через точку (–1,–1), для которой отрезок, отсекаемый касательной к кривой в любой ее точке на оси абсцисс, равен квадрату точки касания.
15. Найти семейство линий, касательные к которым отсекают от оси абсцисс отрезки, равные ординате точки касания.
16. Найти линию, проходящую через точку (0,2), для которой угловой коэффициент касательной в каждой точке линии равен сумме абсциссы и ординаты точки касания.
17. Найти линию, проходящую через точку (2,0) и обладающую тем свойством, что отрезок касательной между точкой касания и осью ординат имеет постоянную длину, равную двум.
18. Найти линию, у которой площадь прямоугольника, построенного на абсциссе любой точки и начальной ординате касательной в этой точке, равна a 2.
19. Тело движется со скоростью v, пропорциональной квадрату времени. Установить зависимость между пройденным путем s и временем t, если известно, что при t =0, s = s 0.
20. Найти линию, проходящую через точку (3,4), у которой отрезок касательной, заключенный между осями координат, делится пополам в точке касания.
21. Определить путь s, пройденный телом за время t, если известно, что скорость в каждый момент времени пропорциональна пройденному пути. Тело проходит 30 м за 1 мин., а 90 м — за 2 мин.
22. За какое время тело, нагретое до 1000, охладится до 250, в комнате с t =200, если до 600 оно охлаждается за 10 мин? (По закону Ньютона скорость охлаждения тела пропорциональна разности между температурой тела и температурой среды).
23. Найти линию, проходящую через точку (1,–2), для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
24. Тело движется по прямой так, что его скорость в каждый момент времени равна корню квадратному из пути, пройденному телом к этому моменту. Найти путь, пройденный телом до момента 10с, если до начала отсчета оно прошло путь 1 м.
25. Найти линию, проходящую через точку (1,1), для которой угловой коэффициент касательной в каждой точке линии обратно пропорционален корню квадратному из ординаты точки касания.