Перечень вопросов по теме
1. Область определения функции нескольких переменных. Частное и полное приращение.
2. Предел и непрерывность функции нескольких переменных.
3. Частные производные и полный дифференциал. Производные и дифференциалы высших порядков.
4. Дифференцирование сложных и неявных функций.
5. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
6. Условный экстремум. Метод наименьших квадратов.
Задание 5. Вычислить частные производные первого и второго порядков указанных функций.
| 0. | 0.1. | 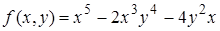 ; ;
| 0.2. |  . .
|
Решение варианта 0.
Пример 0.1. Считая одну из переменных постоянной величиной, с помощью таблицы производных получаем:
 ,
,
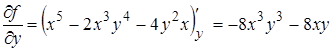 ,
,
 ,
,
 ,
,
 .
.
Пример 0.2. Как и в предыдущем случае, имеем:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
| 1. | 1.1. |  ; ;
| 1.2. |  . .
|
| 2. | 2.1. |  ; ;
| 2.2. |  . .
|
| 3. | 3.1. |  ; ;
| 3.2. |  . .
|
| 4. | 4.1. | 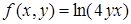 ; ;
| 4.2. | 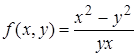 . .
|
| 5. | 5.1. |  ; ;
| 5.2. |  . .
|
| 6. | 6.1. | 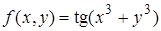 ; ;
| 6.2. |  . .
|
| 7. | 7.1. |  ; ;
| 7.2. | 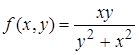 . .
|
| 8. | 8.1. | 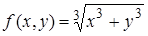 ; ;
| 8.2. |  . .
|
| 9. | 9.1. |  ; ;
| 9.2. |  . .
|
| 10. | 10.1. |  ; ;
| 10.2. | 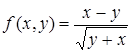 . .
|
| 11. | 11.1. |  ; ;
| 11.2. |  . .
|
| 12. | 12.1. |  ; ;
| 12.2. |  . .
|
| 13. | 13.1. |  ; ;
| 13.2. |  . .
|
| 14. | 14.1. |  ; ;
| 14.2. |  . .
|
| 15. | 15.1. |  ; ;
| 15.2. |  . .
|
| 16. | 16.1. |  ; ;
| 16.2. |  . .
|
| 17. | 17.1. |  ; ;
| 17.2. |  . .
|
| 18. | 18.1. | 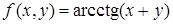 ; ;
| 18.2. | 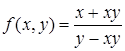 . .
|
| 19. | 19.1. | 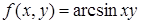 ; ;
| 19.2. |  . .
|
| 20. | 20.1. |  ; ;
| 20.2. |  . .
|
| 21. | 21.1. |  ; ;
| 21.2. |  . .
|
| 22. | 22.1. |  ; ;
| 22.2. |  . .
|
| 23. | 23.1. |  ; ;
| 23.2. |  . .
|
| 24. | 24.1. | 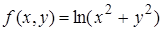 ; ;
| 24.2. | 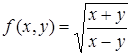 . .
|
| 25. | 25.1. |  ; ;
| 25.2. |  . .
|
Задание 6. Найти локальные экстремумы (первая функция) и условные экстремумы в указанной области (вторая функция).
| 0. | 0.1. 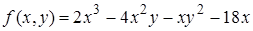 ; ;
|
0.2.  , , 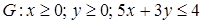 . .
|
Решение варианта 0.
Пример 0.1. Ищем стационарные точки функции:




 .
.
Находим частные производные второго порядка:
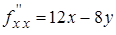 ,
,  ,
,  .
.
Для каждой стационарной точки вычисляем D:
 ,
,  ,
,  ,
,
 ;
;
 ,
,  ,
,  ,
,
 ;
;
Так как в обеих точках D<0, то в них нет экстремума.
Пример 0.2. Как и в предыдущем примере ищем стационарные точки функции в области:


 .
.
Внутрь нашей области попадает только точка (3/20; 1/2), в которой значение исследуемой функции равно 9/320.
Исследуем теперь поведение функции на границе области. На отрезках [(0; 0); (4/5; 0)] и [(0; 0); (0; 4/3)] функция равна нулю, поэтому минимальное и максимальное значение здесь — ноль. На отрезке [(0; 4/3); (4/5; 0)] функция превращается в
 ,
,
исследуя которую, находим  ,
,  .
.
Таким образом,
 ,
,  .
.
| 1. | 1.1. 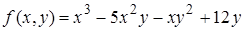 ; ;
|
1.2.  , , 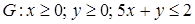 . .
|
| 2. | 2.1. 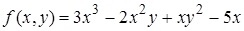 ; ;
|
2.2.  , , 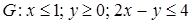 . .
|
| 3. | 3.1.  ; ;
|
3.2. 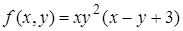 , ,  . .
|
| 4. | 4.1.  ; ;
|
4.2.  , ,  . .
|
| 5. | 5.1.  ; ;
|
5.2.  , ,  . .
|
| 6. | 6.1. 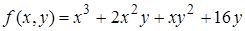 ; ;
|
6.2. 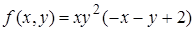 , , 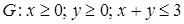 . .
|
| 7. | 7.1.  ; ;
|
7.2.  , ,  . .
|
| 8. | 8.1.  ; ;
|
8.2.  , ,  . .
|
| 9. | 9.1.  ; ;
|
9.2. 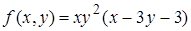 , ,  . .
|
| 10. | 10.1.  ; ;
|
10.2.  , ,  . .
|
| 11. | 11.1.  ; ;
|
11.2.  , ,  . .
|
| 12. | 12.1.  ; ;
|
12.2.  , ,  . .
|
| 13. | 13.1.  ; ;
|
13.2. 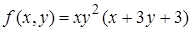 , ,  . .
|
| 14. | 14.1.  ; ;
|
14.2.  , ,  . .
|
| 15. | 15.1.  ; ;
|
15.2.  , , 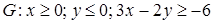 . .
|
| 16. | 16.1.  ; ;
|
16.2.  , , 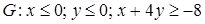 . .
|
| 17. | 17.1.  ; ;
|
17.2.  , ,  . .
|
| 18. | 18.1.  ; ;
|
18.2.  , , 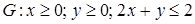 . .
|
| 19. | 19.1.  ; ;
|
19.2.  , ,  . .
|
| 20. | 20.1.  ; ;
|
20.2. 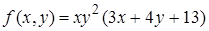 , ,  . .
|
| 21. | 21.1. 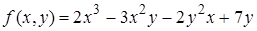 ; ;
|
21.2.  , ,  . .
|
| 22. | 22.1.  ; ;
|
22.2.  , , 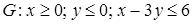 . .
|
| 23. | 23.1.  ; ;
|
23.2. 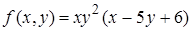 , ,  . .
|
| 24. | 24.1.  ; ;
|
24.2.  , ,  . .
|
| 25. | 25.1.  ; ;
|
25.2.  , ,  . .
|
Ряды
Перечень вопросов по теме
1. Числовые ряды.
2. Сходимость числовых рядов.
3. Признаки сходимости рядов с положительными членами.
4. Знакопеременные ряды. Действия над рядами.
5. Степенные ряды, радиус сходимости, область сходимости.
Задание 7. Исследовать ряды на сходимость.
| 0. | 0.1. | 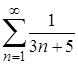 ; ;
| 0.2. |  ; ;
|
| 0.3. |  ; ;
| 0.4. |  . .
|
Решение варианта 0.
Пример 0.1. Используем признак сравнения в предельной форме, сравнив данный ряд с гармоническим. Так как
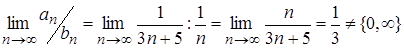 ,
,
то данный ряд расходится в силу расходимости гармонического ряда.
Пример 0.2. Используем признак Даламбера:
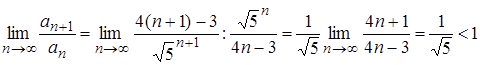 ,
,
значит, данный ряд сходится.
Пример 0.3. Применяя признак Коши, получим:
 ,
,
что свидетельствует о сходимости исследуемого ряда.
Пример 0.4. Данный ряд — знакопеременный, поэтому для исследования его сходимости используем признак Лейбница. Последовательность  монотонно стремится к нулю при росте n:
монотонно стремится к нулю при росте n:
 ,
,  .
.
Таким образом, условия сходимости выполнены.
| 1. | 1.1. | 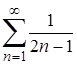 ; ;
| 1.2. |  ; ;
|
| 1.3. | 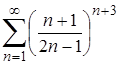 ; ;
| 1.4. |  . .
|
| 2. | 2.1. | 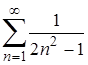 ; ;
| 2.2. | 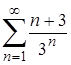 ; ;
|
| 2.3. |  ; ;
| 2.4. |  . .
|
| 3. | 3.1. |  ; ;
| 3.2. |  ; ;
|
| 3.3. |  ; ;
| 3.4. |  . .
|
| 4. | 4.1. |  ; ;
| 4.2. | 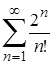 ; ;
|
| 4.3. |  ; ;
| 4.4. |  . .
|
| 5. | 5.1. |  ; ;
| 5.2. |  ; ;
|
| 5.3. |  ; ;
| 5.4. |  . .
|
| 6. | 6.1. |  ; ;
| 6.2. |  ; ;
|
| 6.3. |  ; ;
| 6.4. |  . .
|
| 7. | 7.1. | 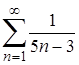 ; ;
| 7.2. |  ; ;
|
| 7.3. |  ; ;
| 7.4. | 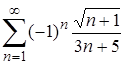 . .
|
| 8. | 8.1. |  ; ;
| 8.2. |  ; ;
|
| 8.3. |  ; ;
| 8.4. |  . .
|
| 9. | 9.1. |  ; ;
| 9.2. |  ; ;
|
| 9.3. |  ; ;
| 9.4. |  . .
|
| 10. | 10.1. |  ; ;
| 10.2. |  ; ;
|
| 10.3. |  ; ;
| 10.4. |  . .
|
| 11. | 11.1. |  ; ;
| 11.2. |  ; ;
|
| 11.3. |  ; ;
| 11.4. |  . .
|
| 12. | 12.1. | 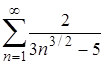 ; ;
| 12.2. |  ; ;
|
| 12.3. |  ; ;
| 12.4. |  . .
|
| 13. | 13.1. |  ; ;
| 13.2. | 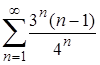 ; ;
|
| 13.3. |  ; ;
| 13.4. |  . .
|
| 14. | 14.1. | 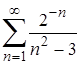 ; ;
| 14.2. |  ; ;
|
| 14.3. |  ; ;
| 14.4. |  . .
|
| 15. | 15.1. |  ; ;
| 15.2. |  ; ;
|
| 15.3. |  ; ;
| 15.4. |  . .
|
| 16. | 16.1. |  ; ;
| 16.2. | 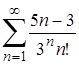 ; ;
|
| 16.3. |  ; ;
| 16.4. | 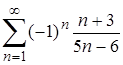 . .
|
| 17. | 17.1. | 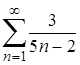 ; ;
| 17.2. | 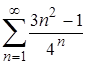 ; ;
|
| 17.3. |  ; ;
| 17.4. |  . .
|
| 18. | 18.1. |  ; ;
| 18.2. |  ; ;
|
| 18.3. | 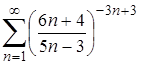 ; ;
| 18.4. |  . .
|
| 19. | 19.1. |  ; ;
| 19.2. |  ; ;
|
| 19.3. | 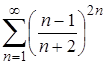 ; ;
| 19.4. |  . .
|
| 20. | 20.1. |  ; ;
| 20.2. |  ; ;
|
| 20.3. |  ; ;
| 20.4. |  . .
|
| 21. | 21.1. |  ; ;
| 21.2. |  ; ;
|
| 21.3. |  ; ;
| 21.4. |  . .
|
| 22. | 22.1. |  ; ;
| 22.2. |  ; ;
|
| 22.3. | 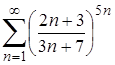 ; ;
| 22.4. |  . .
|
| 23. | 23.1. |  ; ;
| 23.2. |  ; ;
|
| 23.3. |  ; ;
| 23.4. | 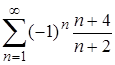 . .
|
| 24. | 24.1. |  ; ;
| 24.2. |  ; ;
|
| 24.3. | 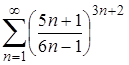 ; ;
| 24.4. |  . .
|
| 25. | 25.1. |  ; ;
| 25.2. |  ; ;
|
| 25.3. | 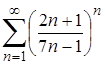 ; ;
| 25.4. |  . .
|