| 0. | 0.1. |  , y (0) = 2; , y (0) = 2;
| 0.2. | (y 4 – 2 x 3 y) dx + (x 4 – 2 xy 3) dy = 0. |
Решение варианта 0.
Пример 0.1. Предполагая, что y ≠ 0, разделим обе части уравнения на y и умножим на x. Получим:  .Данное уравнение можно переписать так:
.Данное уравнение можно переписать так:  . Это уже уравнение с разделенными переменными. Взяв интегралы от обеих частей, получим общее решение:
. Это уже уравнение с разделенными переменными. Взяв интегралы от обеих частей, получим общее решение:
ln6 y 6 = 0,5sin x 2 + lnC.
(В последней записи произвольная постоянная обозначена не С, а lnC. Причина этого становится понятной при выполнении потенциирования последнего равенства). Далее находим:
y (x) = C  .
.
Непосредственной подстановкой в исходное уравнение убеждаемся, что функция у =0 является его решением. Очевидно, что это решение получается из последнего равенства при С = 0. Таким образом, общее решение рассматриваемого уравнения имеет вид: y (x) = C  .
.
Найдем указанное частное решение, для чего определим значение параметра С. Подставляя в последнее выражение x =0 и y = 2, получаем 2 = Сe 0, откуда С = 2. Следовательно, искомое частное решение определяется формулой
y = 2  .
.
Пример 0.2. Функции P (x, y) = y 4 – 2 x 3 y; Q (x, y) = x 4 – 2 xy 3 являются однородными функциями четвертого порядка. Вводим новую переменную u по формуле y = ux, тогда dy = udx + xdu. Преобразуем исходное уравнение, подставив в него выражения для y и dy:
(u 4 + u) dx – (1 – 2 u 3) xdu = 0, или

Проинтегрируем последнее уравнение: ln6 x 6 = ln6 u 6 – ln61+ u 36 + ln6 C 6, откуда x (1 + u 3) = Cu. Поскольку u = y / x, то x 3 + y 3 – Cxy = 0 – общий интеграл данного уравнения.
| 1. | 1.1. | (2 x + 5) dy + ydx =0, y (2) = 0; | 1.2. |  = y/x + ey/x. = y/x + ey/x.
|
| 2. | 2.1. | yx –  =0, =0,  y (0) = 10; y (0) = 10;
| 2.2. | (2 x – y) dx + (x + y) dy =0. |
| 3. | 3.1. |  = (2 x + 2) = (2 x + 2)  , y (0) = 1; , y (0) = 1;
| 3.2. |  = =  . .
|
| 4. | 4.1. | (1 + x 2) dy – 2 xydx = 0, y (0) = 1; | 4.2. | (x + y) dx + xdy =0. |
| 5. | 5.1. |  = y 2cos x, y (0) = 2; = y 2cos x, y (0) = 2;
| 5.2. | (x 2 – y 2) dy – 2 xydx = 0. |
| 6. | 6.1. | x (1 + y 2) dx= y (1 + x 2) dy, y (1)=0; | 6.2. | (x 2 + y 2) dx – 2 xydy = 0. |
| 7. | 7.1. | (1 + y) dx = (1 – x) dy, y (–2) = 3; | 7.2. | (x 2 + y 2) dx – 2 x 2 dy = 0. |
| 8. | 8.1. | x (1 + y 2) dx = ydy, y (0) = 1; | 8.2. | (2  – x) dy + ydx = 0. – x) dy + ydx = 0.
|
| 9. | 9.1. |  = =  , y (1) = 2; , y (1) = 2;
| 9.2. | xy 2 dy = (x 3 + y 3) dx. |
| 10. | 10.1. | (x + xy 2) dx = (x 2 y – y) dy, y (0)=1; | 10.2. | (x 2 – y 2) dx + xydy = 0. |
| 11. | 11.1. |  (4 – x 2) – 4 y = 0, y (0) = 5; (4 – x 2) – 4 y = 0, y (0) = 5;
| 11.2. | (y 2 – xy) dx = (2 xy – x 2) dy. |
| 12. | 12.1. |  – 2 xy – y = 0, y (0) = – 2 xy – y = 0, y (0) =  ; ;
| 12.2. | x  = y ln( = y ln( ). ).
|
| 13. | 13.1. |  dy – ydx = 0, y (1,5) = 1; dy – ydx = 0, y (1,5) = 1;
| 13.2. | x  = y + = y +  . .
|
| 14. | 14.1. | 2 dy – (1 + 4 y 2) dx = 0, y ( ) = 1; ) = 1;
| 14.2. | 2 x 2  = 3 x 2 + 6 xy + y 2. = 3 x 2 + 6 xy + y 2.
|
| 15. | 15.1. | x  = e – x = e – x  , y (0) = 0; , y (0) = 0;
| 15.2. | x 2 dy = (x 2 + xy + y 2) dx. |
| 16. | 16.1. | dy = (1 + 2 y) dx, y (ln2) = 2,5; | 16.2. | x 2  = xy + y 2. = xy + y 2.
|
| 17. | 17.1. |  tg x = 1 + 2 y, y ( tg x = 1 + 2 y, y ( ) = 0,5; ) = 0,5;
| 17.2. | (y +  ) dx = xdy. ) dx = xdy.
|
| 18. | 18.1. |  dy – ydx = dx, y (0) = 0; dy – ydx = dx, y (0) = 0;
| 18.2. | x 3 dy = (x 2 – y 2) ydx. |
| 19. | 19.1. |  x + x +  = 0, y (1) = 0; = 0, y (1) = 0;
| 19.2. | (y –2  ) dx = xdy. ) dx = xdy.
|
| 20. | 20.1. | 2 x 2 ydy = (1 + x 2) dx, y (1) = 2; | 20.2. | (x + y)2 dx = xydy – y 2 dx. |
| 21. | 21.1. | (2 xy + 3y)  = 1 – y 2, y (0) = 2; = 1 – y 2, y (0) = 2;
| 21.2. | (x 2 + y 2)  = 2 xy. = 2 xy.
|
| 22. | 22.1. |  x + y = y 2, y (1) = 0,5; x + y = y 2, y (1) = 0,5;
| 22.2. | (x – y) dx + (x + y) dy =0. |
| 23. | 23.1. | (x 2 – 1)  +2 xy 2 = 0, y (0) = 1; +2 xy 2 = 0, y (0) = 1;
| 23.2. | (y +  ) dx = xdy. ) dx = xdy.
|
| 24. | 24.1. |  dx=xdy, y (1) = 0,5; dx=xdy, y (1) = 0,5;
| 24.2. | x  = y (1 + ln( = y (1 + ln( )). )).
|
| 25. | 25.1. | (1 + ex) y  = ex, y (0) = 1; = ex, y (0) = 1;
| 25.2. |  = = 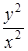 – –  . .
|
Задание 10. Решить следующие линейные дифференциальные уравнения первого порядка.
0.  – y tg x = 2tg x.
– y tg x = 2tg x. 
Решение варианта 0.
Данное уравнение является линейным дифференциальным уравнением первого порядка. Будем искать общее решение уравнения в виде y (x) = u (x) v (x), где u (x) и v (x) – подлежащие определению пока неизвестные функции. Подставляя это выражение в уравнение, получим  , или
, или  . Выберем функцию v (x) так, чтобы выражение в скобках равнялось нулю. Имеем:
. Выберем функцию v (x) так, чтобы выражение в скобках равнялось нулю. Имеем:
 ,
,  ,
,  ,
, 
(Из всей совокупности решений этого уравнения выбрано в качестве функции v одно конкретное). Далее получаем:  ,
,  , откуда u = – 2cos x + C. Таким образом, общее решение имеет вид:
, откуда u = – 2cos x + C. Таким образом, общее решение имеет вид: 
1.  + y = 5 x. + y = 5 x.
| 2.  + y – x = 5. + y – x = 5.
|
3. x  – y = x 3. – y = x 3.
| 4.  –4 y = e 2 x . –4 y = e 2 x .
|
5. x  – 4 y = 2 x 2 – 3 x. – 4 y = 2 x 2 – 3 x.
| 6. x  = x 4 – 2 y. = x 4 – 2 y.
|
7. x 2 = 2 xy + 3. = 2 xy + 3.
| 8.  + y = ex. + y = ex.
|
9.  + y = ex sin x. + y = ex sin x.
| 10. x  + y = sin x. + y = sin x.
|
11. x  – y =x – y =x  . .
| 12. x  + y = ln x + 1. + y = ln x + 1.
|
13. x  – 2 y = 2 x 4. – 2 y = 2 x 4.
| 14.  + y tg x = (cos x)–1. + y tg x = (cos x)–1.
|
15.  – –  = x 2. = x 2.
| 16.  – –  = (x + 1)3. = (x + 1)3.
|
17.  +2 y = e 3 x . +2 y = e 3 x .
| 18.  + y = cos x. + y = cos x.
|
19.  + x 2 y = x 2. + x 2 y = x 2.
| 20. x 2 + xy + 1 = 0. + xy + 1 = 0.
|
21.  + + 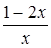 y = 1. y = 1.
| 22.  – y tg x = – y tg x =  . .
|
23. x  – xy = ex. – xy = ex.
| 24.  – 2 y = e–x. – 2 y = e–x.
|
25.  = 2 y + ex – x. = 2 y + ex – x.
|
Задание 11. Решить следующие дифференциальные уравнения второго порядка.
0. 2 y  +
+  = 0.
= 0. 
Решение варианта 0.
Полагая
 = p,
= p,  ,
,
получаем уравнение с разделяющимися переменными 2 yp 3 + 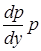 = 0, откуда
= 0, откуда
2 yp 2 +  = 0,
= 0,  = – 2ydy,
= – 2ydy,  = y 2 + C 1, p =
= y 2 + C 1, p =  .
.
Следовательно,
 , (y 2 + C 1) dy = dx.
, (y 2 + C 1) dy = dx.
Интегрируя последнее равенство, находим
 ,
,  .
.
1.  =2 y =2 y  . .
| 2.  = ey. = ey.
|
3.  =2 – y. =2 – y.
| 4.2 = e 2 y . = e 2 y .
|
5. x  = 1 + x 2. = 1 + x 2.
| 6.2 =3 y 2. =3 y 2.
|
7. x  – –  = 0. = 0.
| 8.  cos2 x = 1. cos2 x = 1.
|
9.(x 2 + 1) – 2 x – 2 x  = 0. = 0.
| 10.  =4cos2 x. =4cos2 x.
|
11.  + +   = 0. = 0.
| 12.  = =  . .
|
13.(x 2 + 1) =3. =3.
| 14. x  – –  = x 2 ex. = x 2 ex.
|
15.2 y  =1 + =1 +  . .
| 16. x 2 =4. =4.
|
17.  (2 (2  + x) = 1. + x) = 1.
| 18. x ( +1) + +1) +  = 0. = 0.
|
19.(1 – x 2) – x – x  = 0. = 0.
| 20. y  – –  = 0. = 0.
|
21.  x ln x = x ln x =  . .
| 22. x  + x + x  = 1. = 1.
|
23. y 3 =1. =1.
| 24. y  + +  = 0. = 0.
|
25.  tg y = 2 tg y = 2  . .
|