РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
С ЗАДАННОЙ ТОЧНОСТЬЮ.
Общий вид краевой задачи на отрезке для ОДУ второго порядка.
Краевая задача на отрезке 
для дифференциального уравнения второго порядка в общем случае представима в виде
(1.1)
Здесь все величины, кроме 
, предполагаются заданными.
Отметим, что существует некоторое бесконечное множество функций, удовлетворяющих приведенному дифференциальному уравнению, и лишь наличие области изменения 
(
– геометрическая характеристика конструкции) и условий на краях области обеспечивает единственность его решения. Однако и это решение (хотя оно и единственное), в общем случае, нельзя представить в аналитической форме. Поэтому, как правило, задача решается численным методом.
Метод конечных разностей.
Метод конечных разностей (МКР) – это наиболее простой и при этом достаточно эффективный способ численного решения краевой задачи. Его суть кратко опишем ниже.
Разобьем отрезок 
на 
отрезков (рис. 1.1).
Рис. 1.1. Схема аппроксимации по методу конечных разностей.
Введем обозначения: 
– координаты точек разбиения (узлов); 
– номер точки разбиения (
);
(1.2)
– длина -го отрезка (шаг разбиения);
(1.3)
– «средний» шаг;
, при этом 
, 
; (1.4)
; 
; 
. (1.5)
Производные в -ой точке заменим разностными соотношениями:
(1.6)
– правая разность;
(1.7)
– левая разность;
(1.8)
– центральная разность.
При 
в соответствии с известным определением производной все три величины будут стремиться к 
. Использование той или другой из них зависит от конкретной ситуации.
Вторая производная в -ой точке может быть приближенно представлена разностным отношением в виде разности от первых (вторая производная – это первая производная от первой производной), например
. (1.9)
При 
формулу второй разности можно упростить:
. (1.10)
Пользуясь приведенными обозначениями и формулами, можно представить задачу (1.1) в каждой -ой точке относительно величин 
следующим образом:
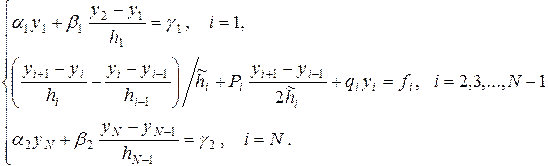(1.11)
Это и есть разностный аналог краевой задачи (1.1). Здесь 
неизвестных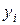 
и линейных уравнений. Приводя подобные члены, получим систему линейных алгебраических уравнений относительно неизвестных величин :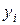
(1.12)
или в матричном виде
, (1.13)
где
; 
; 
,
(1.14)
при этом элементы матрицы и вектора правой части определяются формулами
, 
; 
, 
,
, 
; 
, 
; (1.15)
; 
, ; 
. (1.16)
Следует отметить, что матрица 
трехдиагональная.
После решения системы (1.13) получим приближенное решение задачи (1.1) – значения искомой функции 
в -х точках. Соединяя ломаной линией, получаем приближенное решение 
во всех точках области 
.
Точность решения задачи (1.1) зависит от точности аппроксимации значений производных разностями, которая, в свою очередь, зависит от величины шага разбиения.
Порядок аппроксимации производных.
Для упрощения оценок предположим, что 
. По формуле Тейлора получим:
,
где 
. (1.17)
Тогда для правой разности получим
т.е. окончательно
(1.18)
и имеем аппроксимацию первого порядка.
Аналогично для левой разности
,
т.е. также получаем результат (1.18) и первый порядок аппроксимации.
Рассмотрим также центральную разность.
т.е. 
(1.19)
и здесь имеем аппроксимацию второго порядка.
Следовательно, центральная разность является, как правило, более точной аппроксимацией первой производной.
Установим порядок аппроксимации для второй производной. Имеем:
т.е. 
. (1.20)
Итак, имеем аппроксимацию второго порядка. Аналогично можно установить порядок аппроксимации для любой разностной формулы.
1.4. Разностный аналог краевой задачи для случая .
В этом случае вид системы (1.11) упрощается, а именно
(1.21)
Приводя подобные члены, получим
(1.22)
Пример. Методом конечных разностей решить краевую задачу с начальным шагом 
В этом случае
, 
,
; 
; 
,
, 
, 
, 
, 
, 
.
Пример М-файла
function bnp_dif_eq2
global a,global b,global al1,global bt1,global gm1,global al2,global bt2,global gm2
a=input('ввести координату левого конца отрезка a=');
b=input('ввести координату правого конца отрезка b=');
al1=input('ввести параметр alfa1='); bt1=input('ввести параметр beta1=');
gm1=input('ввести параметр gamma1=');
al2=input('ввести параметр alfa2='); bt2=input('ввести параметр beta2=');
gm2=input('ввести параметр gamma2=');
eps=input('ввести значение точности eps=');
kmax=input('ввести максимальное количество пересчетов kmax=');
n0=input('ввести начальное число точек n=');
l=b-a;
n=n0;
[y1,x1]=mkr_bnp_dif_eq2(n);
for k=1:kmax
n=2*n-1;
[y2,x2]=mkr_bnp_dif_eq2(n);
y12=interp1(x1,y1,x2);
zk=norm(y2-y12,inf)/norm(y2,inf);
if zk<eps
break
end
y1=y2;x1=x2;
end
fprintf('\nn=%d\nz%d=%f\n',n,k,zk)
disp('решение:'),disp(y2')
plot(x2,y2),grid on,title('reshenie krajevoj zadachi y=y(x)')
function [y,xi]=mkr_bnp_dif_eq2(n)
global a,global b,global al1,global bt1,global gm1,global al2,global bt2,global gm2
l=b-a; h=l/(n-1); xi=(a:h:b)'; x=xi(2:n-1);
P=3*x;
q=2+abs(x);
f=2-x;
tm=1/h^2-P/(2*h);
t0=q-2/h^2;
tp=1/h^2+P/(2*h);
A=diag([tm;-bt2/h],-1)+diag([al1-bt1/h;t0;al2+bt2/h])+diag([bt1/h;tp],1);
%disp('матрица системы разностных уравнений'),disp(A)
g=[gm1;f;gm2];
%disp('вектор правой части системы разностных уравнений'),disp(g)
y=A\g;
Результаты решения
ввести координату левого конца отрезка a=-3
ввести координату правого конца отрезка b=3
ввести параметр alfa1=1
ввести параметр beta1=2
ввести параметр gamma1=0
ввести параметр alfa2=1
ввести параметр beta2=0
ввести параметр gamma2=2
ввести значение точности eps=0.001
ввести максимальное количество пересчетов kmax=10
ввести начальное число точек n=61
n=481
z3=0.000690
решение:
Columns 1 through 6
0.5508 0.5474 0.5439 0.5404 0.5368 0.5333
Columns 7 through 12
0.5296 0.5260 0.5223 0.5185 0.5148 0.5109
Columns 13 through 18
0.5071 0.5032 0.4993 0.4953 0.4913 0.4872
Columns 19 through 24
0.4831 0.4789 0.4748 0.4705 0.4662 0.4619
Columns 25 through 30
0.4575 0.4531 0.4486 0.4441 0.4395 0.4349
Columns 31 through 36
0.4303 0.4255 0.4208 0.4159 0.4111 0.4061
Columns 37 through 42
0.4012 0.3961 0.3911 0.3859 0.3807 0.3755
Columns 43 through 48
0.3702 0.3648 0.3594 0.3540 0.3485 0.3429
Columns 49 through 54
0.3373 0.3316 0.3259 0.3201 0.3143 0.3085
Columns 55 through 60
0.3025 0.2966 0.2906 0.2845 0.2784 0.2723
Columns 61 through 66
0.2661 0.2599 0.2537 0.2474 0.2411 0.2348
Columns 67 through 72
0.2285 0.2221 0.2158 0.2094 0.2031 0.1967
Columns 73 through 78
0.1904 0.1841 0.1778 0.1715 0.1653 0.1592
Columns 79 through 84
0.1531 0.1471 0.1411 0.1353 0.1296 0.1240
Columns 85 through 90
0.1185 0.1132 0.1080 0.1030 0.0982 0.0937
Columns 91 through 96
0.0893 0.0853 0.0815 0.0780 0.0748 0.0720
Columns 97 through 102
0.0695 0.0675 0.0658 0.0647 0.0640 0.0638
Columns 103 through 108
0.0642 0.0652 0.0668 0.0691 0.0721 0.0758
Columns 109 through 114
0.0803 0.0857 0.0919 0.0990 0.1071 0.1163
Columns 115 through 120
0.1264 0.1378 0.1503 0.1640 0.1790 0.1954
Columns 121 through 126
0.2131 0.2324 0.2532 0.2756 0.2996 0.3254
Columns 127 through 132
0.3530 0.3824 0.4138 0.4472 0.4827 0.5204
Columns 133 through 138
0.5602 0.6024 0.6470 0.6940 0.7436 0.7958
Columns 139 through 144
0.8506 0.9083 0.9687 1.0321 1.0985 1.1680
Columns 145 through 150
1.2406 1.3164 1.3955 1.4780 1.5639 1.6533
Columns 151 through 156
1.7463 1.8430 1.9433 2.0474 2.1553 2.2670
Columns 157 through 162
2.3827 2.5024 2.6261 2.7538 2.8857 3.0217
Columns 163 through 168
3.1619 3.3062 3.4548 3.6076 3.7647 3.9260
Columns 169 through 174
4.0916 4.2615 4.4356 4.6139 4.7965 4.9832
Columns 175 through 180
5.1741 5.3692 5.5683 5.7715 5.9787 6.1897
Columns 181 through 186
6.4046 6.6233 6.8457 7.0717 7.3012 7.5341
Columns 187 through 192
7.7704 8.0098 8.2523 8.4977 8.7459 8.9968
Columns 193 through 198
9.2503 9.5061 9.7641 10.0242 10.2862 10.5499
Columns 199 through 204
10.8152 11.0818 11.3496 11.6183 11.8879 12.1581
Columns 205 through 210
12.4287 12.6994 12.9702 13.2407 13.5108 13.7802
Columns 211 through 216
14.0488 14.3163 14.5826 14.8473 15.1103 15.3714
Columns 217 through 222
15.6303 15.8869 16.1409 16.3921 16.6403 16.8854
Columns 223 through 228
17.1271 17.3651 17.5995 17.8298 18.0560 18.2779
Columns 229 through 234
18.4953 18.7080 18.9158 19.1187 19.3165 19.5090
Columns 235 through 240
19.6960 19.8775 20.0534 20.2235 20.3877 20.5459
Columns 241 through 246
20.6980 20.8440 20.9837 21.1169 21.2435 21.3634
Columns 247 through 252
21.4764 21.5824 21.6814 21.7732 21.8577 21.9349
Columns 253 through 258
22.0047 22.0670 22.1218 22.1690 22.2086 22.2406
Columns 259 through 264
22.2650 22.2817 22.2908 22.2923 22.2862 22.2725
Columns 265 through 270
22.2513 22.2227 22.1867 22.1434 22.0929 22.0352
Columns 271 through 276
21.9704 21.8987 21.8202 21.7350 21.6432 21.5450
Columns 277 through 282
21.4405 21.3298 21.2131 21.0906 20.9625 20.8288
Columns 283 through 288
20.6898 20.5456 20.3965 20.2427 20.0842 19.9213
Columns 289 through 294
19.7543 19.5832 19.4083 19.2299 19.0480 18.8629
Columns 295 through 300
18.6748 18.4839 18.2904 18.0946 17.8965 17.6964
Columns 301 through 306
17.4944 17.2909 17.0859 16.8797 16.6725 16.4643
Columns 307 through 312
16.2555 16.0461 15.8364 15.6265 15.4166 15.2068
Columns 313 through 318
14.9973 14.7883 14.5798 14.3720 14.1652 13.9593
Columns 319 through 324
13.7545 13.5509 13.3487 13.1479 12.9487 12.7512
Columns 325 through 330
12.5554 12.3615 12.1694 11.9794 11.7914 11.6056
Columns 331 through 336
11.4220 11.2406 11.0616 10.8849 10.7106 10.5387
Columns 337 through 342
10.3693 10.2025 10.0381 9.8764 9.7171 9.5605
Columns 343 through 348
9.4065 9.2551 9.1062 8.9600 8.8164 8.6754
Columns 349 through 354
8.5369 8.4011 8.2678 8.1370 8.0088 7.8831
Columns 355 through 360
7.7599 7.6391 7.5207 7.4048 7.2912 7.1800
Columns 361 through 366
7.0711 6.9644 6.8600 6.7578 6.6577 6.5598
Columns 367 through 372
6.4640 6.3702 6.2785 6.1887 6.1009 6.0149
Columns 373 through 378
5.9309 5.8486 5.7681 5.6894 5.6123 5.5370
Columns 379 through 384
5.4632 5.3910 5.3204 5.2513 5.1836 5.1174
Columns 385 through 390
5.0526 4.9891 4.9270 4.8661 4.8065 4.7482
Columns 391 through 396
4.6910 4.6350 4.5801 4.5263 4.4736 4.4219
Columns 397 through 402
4.3712 4.3215 4.2727 4.2249 4.1780 4.1319
Columns 403 through 408
4.0868 4.0424 3.9988 3.9560 3.9140 3.8727
Columns 409 through 414
3.8321 3.7923 3.7531 3.7145 3.6766 3.6394
Columns 415 through 420
3.6027 3.5666 3.5311 3.4962 3.4618 3.4279
Columns 421 through 426
3.3945 3.3616 3.3293 3.2974 3.2659 3.2349
Columns 427 through 432
3.2044 3.1743 3.1446 3.1153 3.0864 3.0579
Columns 433 through 438
3.0298 3.0020 2.9746 2.9475 2.9208 2.8945
Columns 439 through 444
2.8684 2.8427 2.8173 2.7922 2.7674 2.7429
Columns 445 through 450
2.7187 2.6948 2.6712 2.6478 2.6247 2.6018
Columns 451 through 456
2.5792 2.5569 2.5348 2.5129 2.4913 2.4699
Columns 457 through 462
2.4487 2.4278 2.4071 2.3866 2.3663 2.3462
Columns 463 through 468
2.3263 2.3067 2.2872 2.2679 2.2488 2.2299
Columns 469 through 474
2.2112 2.1926 2.1743 2.1561 2.1381 2.1203
Columns 475 through 480
2.1026 2.0851 2.0678 2.0506 2.0336 2.0167
Column 481
2.0000
>>
Варианты заданий. Методом конечных разностей решить краевую задачу с начальным шагом
1. 
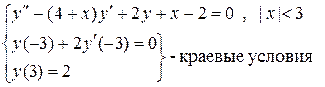
2. 
3. 
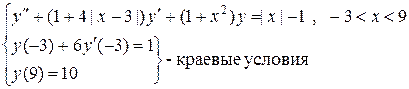
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
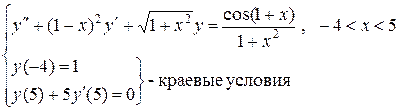
26. 
27. 
28. 
29. 