ПРАКТИЧЕСКИЙ КУРС
ТЕОРЕТИЧЕСКИХ
ОСНОВ
ЭЛЕКТРОТЕХНИКИ
Сборник задач для студентов очной
и дистанционной форм обучения
Часть II
Новосибирск
Коллектив авторов:
Б.В. Литвинов, В.Т. Мандрусова, Ю.В. Петренко, Н.А. Юрьева
Рецензент
канд. техн. наук, зав. кафедрой «Общая электротехника»,
доц. В.В. Богданов
Работа выполнена на кафедре
«Теоретические основы электротехники»
© Новосибирский государственный
технический университет, 2003
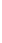I. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
Основные вопросы
1. Законы коммутации.
2. Представление переходной величины в виде суммы принужденной и свободной составляющих.
3. Определение принужденной составляющей.
4. Определение свободной составляющей.
5. Способы составления характеристического уравнения:
а) по дифференциальному уравнению определяемой величины;
б) с помощью алгебраизации системы интегрально-дифференциальных уравнений;
в) с помощью выражения входного сопротивления Z(p).
6. Виды корней и их связь с характером переходного процесса.
7. Определение независимых и зависимых начальных условий.
ЛИТЕРАТУРА
Зевеке Г.В., Ионкин П.А., Нетушил Л.В., Страхов С.В. Основы теории цепей. – М.: Энергия, 1975.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. – М.: Энергия, 1966. – Т. 2. – Гл. 10.
Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1978. – § 283–310.
ПРИМЕРЫ
Задача 1
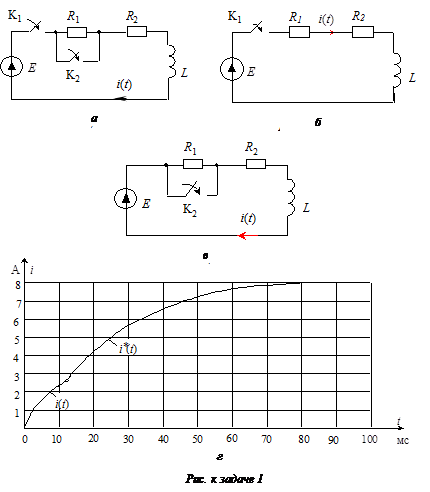
В схеме (рис. а) R1 = R2 = 10 Ом; L = 0,2 Гн; Е = 80 В. Ключ К2 замыкается через 12 мс после замыкания ключа К1 .
Определить переходный ток i(t).
Решение
Так как в цепи поочередно замыкаются два ключа, возникает два переходных процесса, следующих один за другим. Поэтому задача имеет два самостоятельных решения (для временных интервалов 0 £ t £ 12 мс и 12 мс £ t £ ¥). Расчет переходного процесса основан на решении дифференциального уравнения, описывающего режим цепи после коммутации.
Переходный процесс после замыкания ключа К1 (рис. б) (0 £ t £ 12 мс))
· 
Дифференциальное уравнение, характеризующее режим в цепи после коммутации (на основании второго закона Кирхгофа):
|
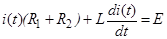. (1)
Общее решение уравнения (1):
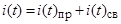. (2)
Принужденная составляющая тока:
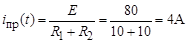. (3)
Характеристическое уравнение дифференциального уравнения (1):
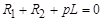, (4)
откуда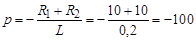 
с–1,
тогда свободная составляющая искомого тока
i св(t) = Ae –100 t . (5)
С учетом (2) переходный ток в рассматриваемом временном диапазоне определится соотношением:
i (t) = 4 + Ae –100 t . (6)
Расчет постоянной интегрирования А. В начальный момент переходного режима (t = 0) выражение (6) принимает вид
. (7)
По первому закону коммутации (ток в индуктивности ни при каких условиях не изменяется скачком)
iL (0 +) = iL (0 -). (8)
До коммутации iL (0 -) = i (0 -) = 0, следовательно, i (0 +) = 0. Тогда соотношение (7) примет вид 0 = 4 + A, откуда А = - 4.
Окончательно, для интервала 
с
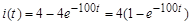А. (9)
Переходный процесс после замыкания ключа К2 (рис. в) (0,012 с £ t £ ¥).
Дифференциальное уравнение для цепи после коммутации (на основании второго закона Кирхгофа):
. (10)
Общее решение уравнения (10):
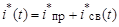. (11)
Принужденная составляющая ток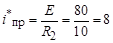а:
А.
Характеристическое уравнение соотношения (10) имеет вид:
R 2 + Lp* = 0, (12)
откуда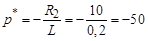 
с–1,
и, как результат, свободная составляющая тока
. (13)
С учетом (11) переходный ток в рассматриваемом временном диапазоне определится соотношением:
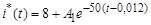. (14)
Расчет постоянной интегрирования А 1:
по закону коммутации для t = 0,012 с
i (0,012-0) = i (0,012+0);
к моменту коммутации К2 искомый ток имел значение (см. (9)):
i (0,012-0) = [4(1- e –100 t )] t = 0,012 = 4(1- e –100×0,012) = 4(1- e –1,2) = 2,8 A.
Следовательно, в начальный момент после коммутации (см. (14)):
i* (0,012+0) = [8 + A 1 e –50(t – 0,012)] t = 0,012 = 8 + A 1,
т.е. 2,8 = 8 + А 1, откуда А 1 = - 5,2.
Окончательно, для временного диапазона 0,012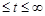 
i* (t) = 8 - 5,2e–50(t –0,012) А.
График переходного тока i (t) (рис. г). Рассчитаем значения переменного тока и занесем в таблицу:
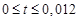
| t, мc | |||||
| i, A | 1,04 | 1,8 | 2,32 | 2,8 | ||
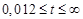
| t, мc | |||||
| i*, A | 2,8 | 3,54 | 6,08 | 7,295 | 7,741 |
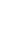Задача 2
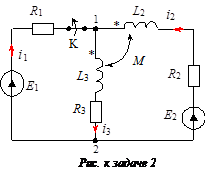В схеме (см. рисунок) известно: E 1 = 30 В; Е 2 = 20 В;
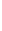L 2 = 0,2 Гн; L 3 = 0,4 Гн;
М = 0,1 Гн; R 1 = 10 Ом;
R 2 = R 3 = 20 Ом.
Определить переходный ток i 3(t).
Решение
После коммутации в цепи (см. рисунок) остается один контур, поэтому i 3(t) =i 2(t) = i (t).
Дифференциальное уравнение, описывающее режим цепи после коммутации c учетом встречного включения индуктивно связанных катушек:
. (1)
Общее решение уравнения (1):
i = i пр + i св. (2)
Принужденная составляющая тока:
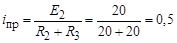А. (3)
Свободная составляющая переходного тока: характеристическое уравнение дифференциального соотношения (1) имеет вид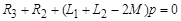 
, откуда
,
и, как результат, свободная составляющая искомого тока
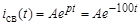. (4)
С учетом (3) и (4) искомый переходный ток определится соотношением:
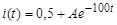. (5)
Расчет постоянной интегрирования. Как следует из (5), в начальный момент после коммутации (t = 0+) имеем
i (0 +) = 0,5 + A. (6)
С учетом того, что рассматриваемая цепь допускает скачки токов в ветвях с индуктивностями (закон коммутации в тривиальной форме неприемлем), для определения начальных условий необходимо использовать обобщенный закон коммутации, в соответствии с которым
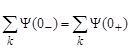. (7)
Применительно к рассматриваемой цепи (см. рисунок), с учетом встречного включения индуктивно связанных катушек, тождество (7) представляется в виде:
(8)
Расчет установившегося докоммутационного режима целесообразно проводить с использованием метода узловых потенциалов. В соответствии с этим методом для цепи (см. рисунок) при исходном положении ключа
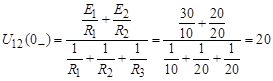В.
Докоммутационные значения токов в индуктивных элементах (на основании закона Ом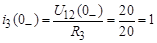а):
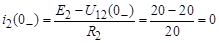А;
А.
В соответствии с (8), значения токов после коммутации (начальные условия):
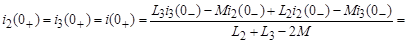
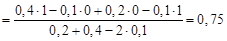А.
Начальное значение переходного тока i (0+) позволяет определить постоянную интегрирования А из тождества (6) 0,75= 0,5+ А, откуда А = 0,25. В результате,
i (t) = 0,5 + 0,25 e –100 t A.
Ответ: i (t) = 0,5 + 0,25 e –100 t A.
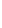Задача 3
В цепи, представленной на рисунке, известно: Е = 100 В; R = 3 Ом; R 1 = 5 Ом; R 2 = 2 Ом.
Определить значения токов в цепи и напряжение на индуктивности в начальный момент после коммутации (t = 0+).
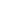
Решение
Начальные значения всех искомых функций могут быть найдены из уравнений, описывающих состояние рассматриваемой цепи (на основе законов Кирхгофа) в начальный момент (t = 0+) переходного процесса:
(1)
До коммутации в рассматриваемой схеме
uc (0–) = 0;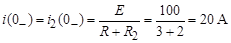 
.
По законам коммутации
uc (0–) = uc (0+) = 0; i 2(0–) = i 2(0+) = 20A.
C учетом законов коммутации, система уравнений (1) принимает вид:
(2)
Из (2) следует i (0+) = 25A; i 3(0+) = 5A; uL (0+) = –15 B.
Ответ: i (0+) = 25A; i 2(0+) = 20A; i 3(0+) = 5A; uL (0+) = –15 B.
Задача 4
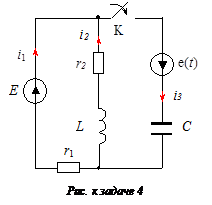В цепи (см. рисунок) известно: Е = 100 В; r 1= 5 Ом; r 2 = 30 Ом; е (t)=169sin(300 t) В; С = 200 мкФ; L = 100 мГн.
Определить i 3(t) после замыкания ключа.
Решение
1. Общее решение искомого тока:
i 3 = i 3пр + i 3св. (1)
2. С учетом того, что постоянный ток через конденсатор не протекает, принужденная составляющая искомого тока обусловлена лишь синусоидальным источником e (t) (сначала определяется комплекс установившегося синусоидального тока, а затем записывается его мгновенное значение):
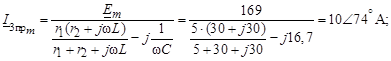
А. (2)
3. Характеристическое уравнение и его корни. Определитель системы алгебраизированных уравнений, составленных по методу контурных токов:
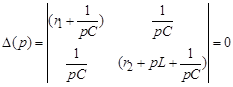
или 
.
Откуда 
и
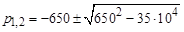; p 1 = - 380 c–1; p 2 = - 920 c–1.
Следовательно, свободная составляющая искомого тока
i 3св = А 1 е – 380 t + А 2 е – 920 t. (3)
4. С учетом (1) – (3) общее решение искомого тока
i 3(t) = 
+ А 1 е – 380 t + А 2 е – 920 t A. (4)
5. Определение постоянных интегрирования. Продифференцируем уравнение (4):
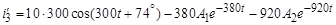(5)
и запишем соотношения (4) и (5) для t = 0+:
i 3(0+) = 10∙sin74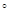 
+ А 1 + А 2 ; (6)
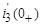= 10∙300∙cos74 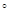– 380A1 – 920A2. (7)
Далее, для вычисления i 3(0+) и i 3´(0+) запишем уравнения состояния рассматриваемой цепи (на основе законов Кирхгофа) для переходного режима:
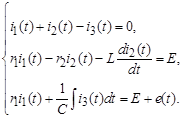(8)
Продифференцируем уравнения (8):
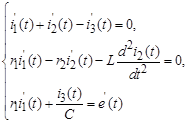(9)
и рассмотрим уравнения (8) и (9) для начального момента переходного режима t = 0+:
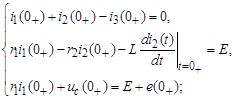(10)
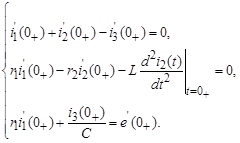(11)
В соответствии с законами коммутации
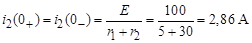; (12)
uc (0+) = uc (0–) = 0. (13)
Cовместное решение уравнений (10) – (13) позволяет определить искомые i 3(0+) и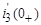 
. Из (10)
;
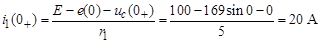i 3(0+) = i 1(0+) – i 2(0+) = 20 – 2,86 = 17,14 А;
uL (0+) = E – r 1 i 1(0+) – r 2 i 2(0+) = 100–5∙20–30∙2,86 = -85,8 B; (14)
В/с. (15)
Из (11), (14), (15)
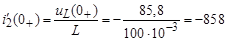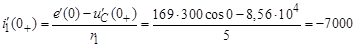А/с;
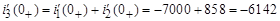А/с;
А/с.
С учетом найденных начальных условий тождества (6) и (7) принимают вид:
17,14 = 10·sin74° + A 1 + A 2; – 6142 = 10∙300∙cos74° – 380 A 1 – 920 A 2
или 7,59 = А 1 + А 2; - 6967 = - 380 А 1 – 920 А 2. Откуда А 1 = 0,145 А; А 2 = 7,34 А. Окончательно
А.
Ответ: 
А.
Задача 5
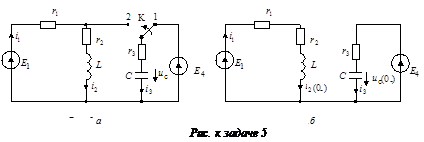
В цепи (рис. а) известно :Е 1 = 120 В; Е 4 = 30 В; r1 = 40 Ом; r2 = r 3 = 20 Ом; L = 0,5 Гн; C = 100 мкФ. В момент времени t = 0 ключ мгновенно перебрасывается из положения 1 в положение 2.
Определить i 1(t).
Решение
1. Общее решение:
i 1(t) = i 1пр + i 1св. (1)
2. Принужденная составляющая:
А.
3. Свободная составляющая.
Характеристическое уравнение получим, приравняв к нулю определитель системы алгебраизированных уравнений, составленных по методу контурных токов:
или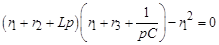 
.
Откуда 
.
Корни характеристического уравнения:
p 1 = (-117 + j 80) c –1; p 2 = (-117 - j 80) c –1.
Выражение для свободной составляющей искомого тока:
.
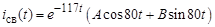4. Общее решение в соответствии с (1):
. (2)
5. Определение постоянных интегрирования. В начальный момент после коммутации выражение (2) имеет вид:
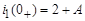. (3)
В качестве дополнительного уравнения для определения постоянных А и В используется выражение для начального значения производной искомого тока:
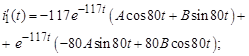
. (4)
Независимые начальные условия определяются на основании законов коммутации: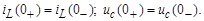 
Докоммутационные значения тока в индуктивности и напряжения на конденсаторе определяются по докоммутационной схеме (рис. б):
А; 
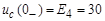В.
Зависимые начальные условия (значения тока i 1(0+) и его производной 
) определяются посредством решения уравнений состояния цепи и их производных, записанных для t = 0+:
(5)
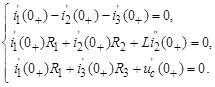(6)
Из совместного решения уравнений (5) и (6) с учетом независимых начальных условий следует:
i 1(0+) = 2,17 A; 
А/с. (7)
Найденные начальные значения тока i 1(0+) и его производной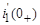 
позволяют определить постоянные интегрирования А и В из тождеств (3) и (4): 2,17 = 2 + А; -32,9 = -117 А + 80 В.
В результате, А = 0,17, В = - 0,162.
6. Окончательное выражение для искомого переходного тока
Ответ: 
А.
Задачи для самостоятельного решения
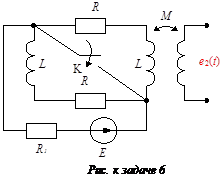
Задача 6
В схеме (см. рисунок) известно: Е = 10 В;
L = 10 –2 Гн;
R = 50 Ом;
R 1 = 100 Ом;
M = 10 –3 Гн.
Определить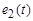 
.
Ответ: 
.
Задача 7
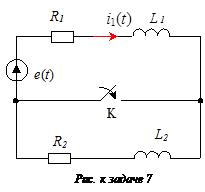
Дано (см. рисунок):
R 1 = 10 Oм;
R2 = 5 Ом;
x 1 = x 2 = 20 Ом;
е (t) = 170 sin(ω t) B;
f = 400 Гц.
Определить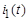 
.
Ответ:
