Задача 5
Найти закон изменения тока в цепи (см. рисунок), если
;
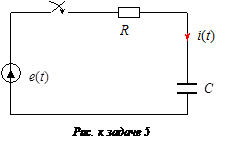
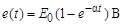E 0 = 100 B;
α = 100 c –1;
R = 50 Ом;
С = 100 мкФ.
Ответ:
i (t) = 2(e –100 t – e –200 t ) A.
Задача 6
Найти закон изменения тока в ветви с источником энергии.
Дано (см. рисунок): E = 100 B; R = 3 Ом; R 1 = 5 Ом; R 2 = 2 Ом; С = 200 мкФ; L = 0,1 Гн.
Ответ: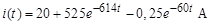 
.
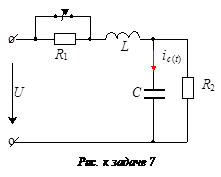Задача 7
Найти закон изменения тока в конденсаторе после размыкания ключа, если (см. рисунок): R 1 = R 2 = 100 Ом; L = 1,0 Гн; С = 100 мкФ;
U = 2000 B.
Ответ: 
.
Задача 8
Дано (см. рисунок):
U (t) = 500 sin 314 t B;
R = 50 Ом;
С = 100 мкФ;
L = 0,3 Гн.
Определить u C(t) по методу Богатырева.
Ответ:
.
III. Расчет переходных процессов
ПРИ ВКЛЮЧЕНИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
НА НАПРЯЖЕНИЕ ПРОИЗВОЛЬНОЙ ФОРМЫ
(интеграл Дюамеля)
Основные вопросы
Интеграл Дюамеля для определения переходных токов и напряжений.
Условия применимости интеграла Дюамеля.
Переходная функция напряжения и переходная проводимость.
Методика решения задачи, когда график изменения напряжения, воздействующего на цепь, содержит разрывы первого рода.
ЛИТЕРАТУРА
Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – М.: Энергия, 1975. – § 13.15, 13.16.
Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1978. – § 8.51 – 8.55.
Примеры
Задача 1
В схеме (см. рисунок) известно: u (t) = 100e –20 t B; R 1 = 10 Ом; R 2 = 15 Ом; L = 0,1 Гн.
Определить i 1(t), используя интеграл Дюамеля.
Решение
В соответствии с основной формой интеграла Дюамеля
.
Определение переходной проводимости g 1(t) искомой ветви (классический метод):
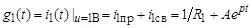=0,1 + Аept,
где 
= 60 с–1;
= 0,04 – 0,1 = - 0,06.
Следовательно, 
Ом–1.
Переходная проводимость в запаздывающей форме:
Ом–1.
|
|
Определение u (0) и u' (x): u (0) = 100B;
u' (x) = u' (t) |t = x = – 2000 e– 20 x B/c.
Искомый переходный ток i 1(t):
.
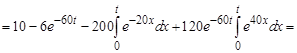
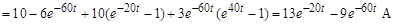Проверка: 
(с учетом закона коммутации);
.
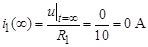Ответ: i 1(t) = 13 e –20 t – 9 e– 60 t A.
Задача 2
В схеме (рис. а) известно: R1 = 10 Ом; R2 = 15 Ом; C = 20 мкФ. График напряжения на входе цепи представлен на рис. б.
; 
; U 0= 100 B; t 1 = 5 мкс;
t 2 = 1,575 мс; ω = 103 c–1.
Определить uC (t).
Решение
Выражения для искомого напряжения для различных временных интервалов, представленные с помощью интеграла Дюамеля:
а) 0 ≤ t ≤ t 1:
;
б) t 1 ≤ t ≤ t 2:
;
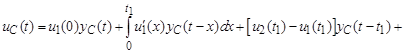
в) t 2 ≤ t ≤ ∞:
.
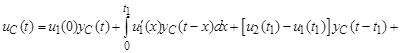
Переходная функция по напряжению 
;
yC (t) =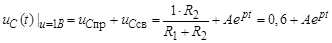 
,
где 
.
Так как 
, то yC (0) =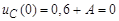 
. Отсюда: А = – 0,6 В и 
;
;
.
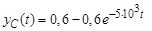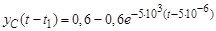Расчет напряжений и их производных:
; 
;
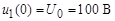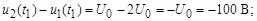
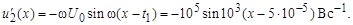
Переходное напряжение на емкости:
а) 
:
.
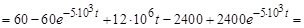
Проверка расчета: uC (0) = 0;
б)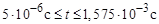 
:
Проверка расчета: uC (t 1-0) = uC (t 1+0);
;
;
в) 
:
= 
.
Проверка расчета: 
;
;
.
Задача 3
В цепи (рис. а) известно: E1 = 100 B; E2 = 50 e5 t B; R1 = 5 Ом; R 2 = 15 Ом; L = 0,5 Гн.
Определить i 1(t).
Решение
Рассматриваемая задача решается двумя способами.
Первый способ расчета: приведение задачи к нулевым начальным условиям.
Искомый переходный ток в цепи с ненулевыми начальными условиями может быть найден как совокупность тока до коммутации i 1(- t) и переходного тока i 10(t) в цепи с нулевыми начальными условиями 
:
а) ток до коммутации 
;
б) переходный ток в схеме (рис. б) с нулевыми начальными условиями. Напряжение на зажимах разомкнутого ключа (до коммутации):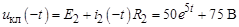 
.
Расчет цепи при нулевых начальных условиях при помощи интеграла Дюамеля:
;
переходная проводимость:
.
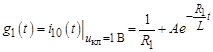Так как 
, то 
и 
Ом–1.
Переходная проводимость в запаздывающей форме:
|
|
Ом–1;
расчет u кл(0) и 
: 
;
;
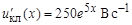переходный ток при нулевых начальных условиях
;
в) искомый переходный ток:
.
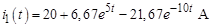Проверка: 
.
Второй способ расчета: метод наложения.
:
а) расчет компонента переходного тока 
, обусловленного источником ЭДС Е 1 (схема рис. в), классическим методом:
.
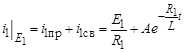Так как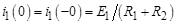 
, то
,
и искомая составляющая переходного тока:
;
б) расчет составляющей переходного тока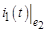 
, обусловленной источником ЭДС е 2 (схема рис. г), с помощью интеграла Дюамеля:
;
; 
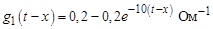
(переходная и запаздывающая проводимости рассчитаны при решении задачи первым способом);
; 
;
.
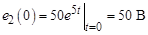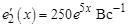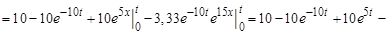
Искомый переходный ток:
.