СВОЙСТВА СТЕПЕННЫХ РЯДОВ

1. На любом отрезке, целиком лежащем внутри интервала сходимости, сумма степенного ряда f(x) есть непрерывная функция.

2. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз, при этом после дифференцирования полученные ряды имеют тот же радиус сходимости.

3. Степенной ряд можно почленно интегрировать в интервале сходимости любое число раз, при этом после интегрирования полученные ряды имеют тот же радиус сходимости.

 

РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ

Всякая функция f (x), бесконечно дифференцируемая в окрестностях точки х=а, может быть разложена в сходящийся степенной ряд Тейлора:

При а =0 получаем ряд Маклорена:

 

Таблица стандартных разложений элементарных функций

в ряд Маклорена*

1.

2.

3.

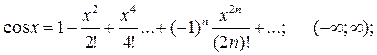
4.

5.

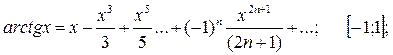
Разложение справедливо: при α≥0 в интервале [-1;1];

при -1<α<0 в интервале ; при α≤0 в интервале .

Частные случаи:

6.1.

6.2.

 

 

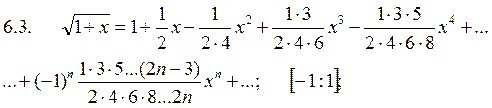
ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ

Вычисление значений функций

Для вычисления приближенного значения функции f(x) ее раскладывают в абсолютно сходящийся степенной ряд (например, в ряд Маклорена):

где S_n – n -ная частичная сумма (сумма первых n членов ряда):

R_n – остаток ряда:

Несколько первых n членов оставляют, а остаток ряда R_n отбрасывают. Чем больше взять членов ряда, тем точнее будет значение функции. Тогда

Для оценки ошибки найденного приближенного значения f(x) необходимо оценить сумму отброшенных членов (остаток ряда) R_n, причем эта сумма по модулю должна быть меньше заданной погрешности δ:

│ R_n │< δ.

Для знакочередующихся рядов остаток ряда R_n меньше первого из отброшенных членов:

│ R_n │< u_{n +1}.

Для рядов с положительными членами R_n высчитывают по различным формулам, конкретным для каждого ряда [1-6].

Пример 6. Пользуясь стандартным разложением cos x в ряд, вычислить cos18^o с точностью до 0,0001.

Решение. Имеем:

Достаточно взять три члена знакочередующегося ряда, так как четвертый член меньше заданной точности: 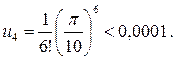Каждый член ряда вычисляем с пятью знаками после запятой. Тогда за первые четыре знака после запятой можно ручаться:

Пример 7. Вычислить с точностью до 0,0001.

Решение. Воспользуемся стандартным разложением (x+ 1) ^α в ряд, полагая х =0,1, α =1/5. Имеем:

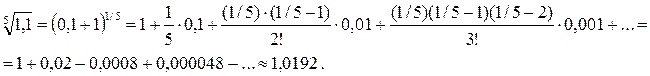Для вычислений достаточно было взять три члена ряда, так как четвертый член меньше заданной точности 0,0001.

Вычисление пределов

Пример 8. Найти предел:

Решение. Заменив ln(х +1) его разложением в степенной ряд, получим:

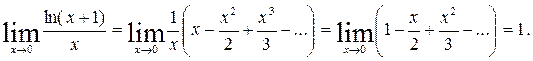
Интегрирование функций

Пример 9. Найти интеграл: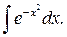

Решение. Разложим подынтегральную функцию в ряд. Для этого в разложении функции е^х подставим вместо х выражение – х ²:

Интегрируя этот ряд почленно, получим:

Вычисление определенных интегралов

Пример 10. Вычислить определенный интеграл 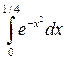с точностью до 0,0001.

Решение. Используя результаты примера 9 и формулу НьютонаЛейбница, получим:

Достаточно взять два члена знакочередующегося ряда, так как третий член меньше заданной точности: