Согласно алгоритмической схемы рассчитываемой системы управления (рис.1), передаточная функция нескорректированной системы имеет вид:
Подставим в формулу (12) численные значения постоянных времени и передаточных коэффициентов элементов системы:
Произведем вспомогательные вычисления, необходимые для построения ЛАЧХ нескорректированной системы Lнс(ω):
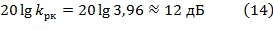
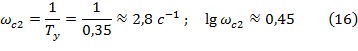
ЛАЧХ нескорректированной (исходной) системы Lнс(ω) представлена на рис.3.
Построим ЛАЧХ скорректированной (желаемой) системы Lск(ω) по заданным показателям качества замкнутой системы в переходном режиме (σ=25 %; t п=3,0 с; М =1,30), предварительно рассчитав параметры среднечастотного участка ЛАЧХ желаемой системы в соответствии с формулами (3.10 с.18 [2]):
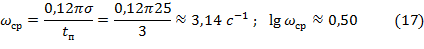
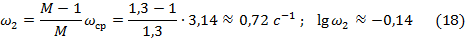
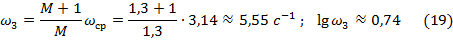
В нашем случае среднечастотный участок ЛАЧХ исходной системы пересёк ЛАЧХ скорректированной системы и, вследствие этого, был «обрезан» до встречи с ЛАЧХ исходной системы.
Рис.3 – К расчету последовательного корректирующего устройства.
Вычтем из ЛАЧХ скорректированной системы ЛАЧХ нескорректированной системы и получим ЛАЧХ последовательного корректирующего устройства (см. рис.3):
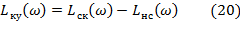
Так как ЛАЧХ корректирующего устройства с увеличением частоты ω имеет тенденцию к увеличению амплитуды до частоты ω3, то для его технической реализации выбираем две последовательно включённые интегро-дифференцирующие rC-цепи с преобладанием дифференцирования, разделенные усилителем рис.4. Усилитель в схеме выполняет роль усиления сигнала и разделения цепей.
| С1 |
| С2 |
| r1 |
| r2 |
| r3 |
| r4 |
| K доп |
| k 1<1 |
| K 2<1 |
| U вх |
| U вых |
Рис.4 – Принципиальная схема последовательного корректирующего устройства.
|
|
Запишем передаточную функцию корректирующего устройства:
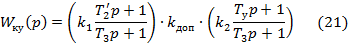
Где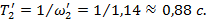 
(значение частоты 
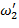снимаем с ЛАЧХ); 
Для того, чтобы передаточный коэффициент системы k рк не изменился, передаточный коэффициент корректирующего устройства должен быть равен единице. Для этого надо выполнить условие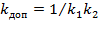 
.
Рассчитаем передаточные коэффициенты k 1, k 2, k доп корректирующего устройства:
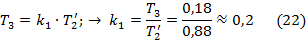
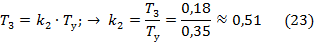
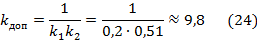
Для расчета параметров элементов корректирующего устройства зададим численные значения следующим параметрам: для первой цепи r1=1 МОм, для второй цепи r3=1 МОм. Рассчитаем остальные параметры по формулам:
- для первой цепи
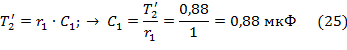
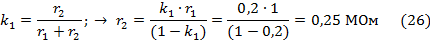
- для второй цепи
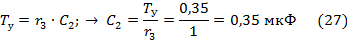
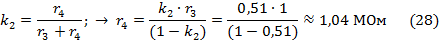
Запишем передаточную функцию разомкнутой скорректированной системы, учитывая, что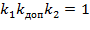 
.
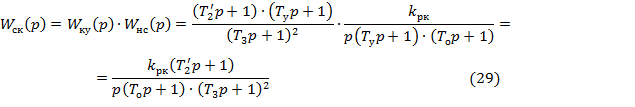
Вычислим фазовый сдвиг скорректированной системы на частоте среза ωср (3.11 стр.18 [2]).
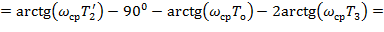
Вычислим запас по фазе ∆ϕ замкнутой скорректированной системы, применив формулу (3.12 стр.18 [2]).
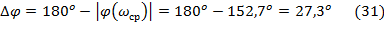
Для определения запаса устойчивости замкнутой системы по амплитуде ∆ L следует сначала найти частоту ωπ, при которой фазовый сдвиг системы будет равен –(180±1)0 (3.13 стр.19 [2]).
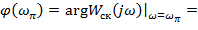
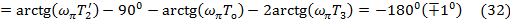
Частоту ωπ из выражения (32) найдем подбором, учитывая, что ωπ > ωср. Найденное таким образом численное значение частоты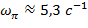 
.
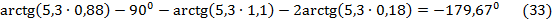
Отложив вычисленное значение частоты ωπ на графике ЛАЧХ скорректированной системы Lск(ω) (рис.3), найдем запас устойчивости замкнутой скорректированной системы по амплитуде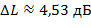 
.