Исходным выражением для построения является характеристическое уравнение замкнутого контура скорректированной системы.
Преобразуем выражение (34) и сгруппируем подобные члены.
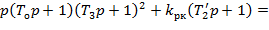
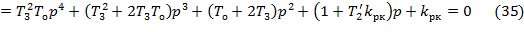
Произведем в уравнении (35) подстановку 
и получим тождество.
В выражении (36) сгруппируем действительную и мнимую части.
a
b
Так как комплексная величина a+jb равна нулю только в том случае, если одновременно равны нулю её действительная и мнимая части, то тождество (37) эквивалентно двум уравнениям.
| (38) |
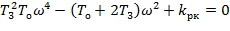
Упорядочим систему уравнений (38) с учетом того, что параметр, стоящий в обоих уравнениях на первом месте, будем откладывать по оси абсцисс, а параметр, стоящий на втором месте, - по оси ординат. Для этого в обоих уравнениях сгруппируем отдельно члены, зависящие и не зависящие от параметров k рк и Т о.
| (39) |
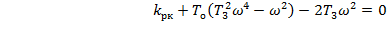
Подставим в систему уравнений (39) численные значения постоянных времени с учетом того, что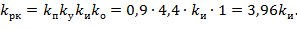 
А1 В1 С1
| (40) |
А2 В2 С2
Решим систему уравнений (40) методом определителей.
Где
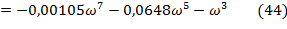
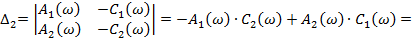
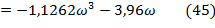
Подставив выражения (43)-(45) в формулы (41) и (42), получим.
Вычислим значения функций 
и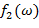 
при изменении частоты ω от нуля до 
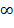и результаты сведем в таблицу 2. Так как функции и 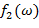являются чётными, то кривая D -разбиения дважды проходит через одни и те же точки (при изменении частоты ω от 
до нуля и от нуля до 
).
Таблица 2 – Граница области устойчивости системы в плоскости параметров k и и Т о.
| ω | K и | T о |
| -0,485625 | ∞ | |
| -0,547629 | -2,613266 | |
| 1,2 | -0,577600 | -2,043737 |
| 1,4 | -0,615394 | -1,712052 |
| 1,6 | -0,662516 | -1,510062 |
| 1,8 | -0,721018 | -1,386806 |
| -0,793730 | -1,316372 | |
| 2,2 | -0,884625 | -1,285317 |
| 2,4 | -0,999424 | -1,287320 |
| 2,6 | -1,146632 | -1,320991 |
| 2,8 | -1,339425 | -1,389449 |
| -1,599319 | -1,501486 | |
| 3,2 | -1,963952 | -1,675243 |
| 3,4 | -2,505587 | -1,947762 |
| 3,6 | -3,382741 | -2,402210 |
| 4,292218 | 1,682955 | |
| 2,340714 | 0,616497 | |
| 1,928144 | 0,347553 | |
| 1,828739 | 0,229962 | |
| 1,854136 | 0,165839 | |
| 1,947827 | 0,126294 | |
| 2,087095 | 0,099893 | |
| 2,261100 | 0,081256 | |
| 2,464044 | 0,067542 | |
| 2,692564 | 0,057122 | |
| 2,944581 | 0,048999 | |
| 3,218752 | 0,042531 | |
| 3,514168 | 0,037290 | |
| 3,830199 | 0,032978 |
На рис.5 изображена кривая D -разбиения, построенная по данным табл.2. Кривую D -разбиения штрихуем по следующим правилам (стр.290 [1]).
Если определитель ∆ > 0, то штриховка наносится слева (при движении вдоль кривой в сторону увеличения ω); если определитель ∆ < 0, то штриховка наносится справа.
Так как при прохождении переменной ω через нуль знак главного определителя ∆ меняется на противоположный, то штриховка кривой D-разбиения всегда двойная.
Рис.5 – Область устойчивости скорректированной системы в плоскости параметров kи и Tо.
Дополним кривую D -разбиения особыми прямыми, уравнения которых имеют следующий вид: a 0=0, отсюда T o=0; a n=0, отсюда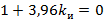 
и 
. Особые прямые штрихуем по следующим правилам (стр.291 [1]).
Особые прямые, соответствующие ωи=0 и ωи= 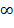, штрихуют один раз. В точках пересечения (или сопряжения) особой прямой с основной кривой D -разбиения, соответствующих ω=ωи, заштрихованные стороны прямой и кривой должны быть обращены друг к другу. Причем, если в точке пересечения определитель ∆ меняет знак, то штриховка особой прямой переходит на противоположную сторону прямой. Если же знак определителя не меняется, то направление штриховки остается прежним.
На рис.5 откладываем точку А с заданными координатами k и и T о (k и=1; T о=1,1). Заданная точка входит в область устойчивости скорректированной системы.