Задача 1. Выбор специализации сельскохозяйственного предприятия
Постановка задачи. Агропромышленное предприятие, не имеющее определенной специализации, занимается разработкой как растениеводческого, так и животноводческого направления. В условиях самофинансирования и жесткой конкуренции перед руководством предприятия встал вопрос о развитии более доходного направления. При оценивании направлений было решено учитывать следующие критерии – затраты ресурсов, затраты труда, прибыль от реализации продукции, объемы внутреннего потребления продукции.
Имеются следующие данные:
| Критерии | Растениеводство | Животноводство |
| Материальные затраты, тыс. руб. | ||
| Затраты труда, тыс. руб. | ||
| Прибыль от реализации продукции, тыс. руб. | ||
| Внутренне потребление, тыс. руб. |
Считается, что все критерии равнозначны.
Методика решения задачи
На первом шаге решения задачи строится иерархия системы:
    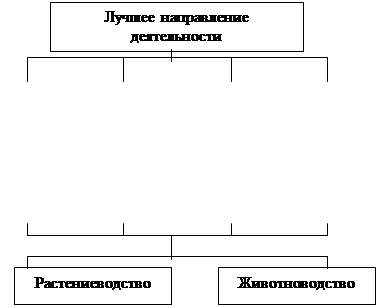 |
Вторым шагом является сравнительное оценивание альтернатив относительно критериев.
Для этого строится матрица попарных сравнений
| Наименование критерия | Альтернатива А1 | Альтернатива А2 | |
| Вес альтернативы А1 | Вес альтернативы А2 | ||
| Альтернатива А1 | Вес альтернативы А1 | Преимущество альтернативы А1 перед альтернативой А2 | |
| Альтернатива А2 | Вес альтернативы А2 | Преимущество альтернативы А2 перед альтернативой А1 |
Преимущество альтернативы считается по формуле:
| Преимущество альтернативы Аi перед альтернативой Aj | = | Вес альтернативы Ai |
| Вес альтернативы Aj |
Если преимущество альтернативы Аi перед альтернативой Aj больше 1, то альтернатива Ai предпочтительнее альтернативы Aj. Ввиду этого веса альтернатив рассчитываются следующим образом:
- если по критерию заданы числовые значения альтернатив и большее значение означает улучшение качества, то в качестве веса берется само числовое значение (например, по критерию «Прибыль от реализации продукции» значение 5460 тыс. руб. лучше, чем значение 2980, а значит, весом альтернативы «Животноводство» будет 5460, а альтернативы «Растениеводство» - 2980. Аналогично рассчитываются веса альтернатив по критерию «Внутреннее потребление»);
- если ситуация обратна ранее рассмотренной, т.е. увеличение значения альтернативы по критерию показывает ухудшение качества, то в качестве веса альтернатив берется величина, обратная их числовому значению (например, по критерию «Материальные затраты» значение 2500 хуже, чем значение 1870, поэтому весом альтернативы «Животноводство» будет значение 1/2500, а для альтернативы «Растениеводство» - 1/1870. По аналогии рассчитываются веса альтернатив по критерию «Затраты труда»).
На третьем шаге рассчитываются локальные приоритеты альтернатив по критериям. Для этого по каждой строке матриц попарных сравнений высчитывается среднее геометрическое элементов строк:
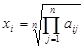 ,
,
где n – количество элементов в строке,
i –номер строки,
aij – элементы строки.
Для матрицы 2´2 локальные приоритеты рассчитываются по формулам:
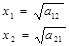 ,
,
где а12 – преимущество альтернативы 1 перед альтернативой 2,
а21 – преимущество альтернативы 2 перед альтернативой 1.
Для локальных приоритетов по одной матрице попарных сравнений должно выполняться правило нормальности – сумма всех локальных приоритетов должна быть равна 1. Если это правило не выполняется, локальные приоритеты необходимо нормализовать. Для этого:
1) подсчитать сумму всех локальных приоритетов по матрице;
2) каждый локальный приоритет разделить на полученную сумму.
Полученные приоритеты принято называть нормализованные локальные приоритеты.
На четвертом шаге необходимо рассчитать локальные приоритеты критериев:
- если критерии не равнозначны, то по ним строится матрица попарных сравнений;
- если критерии равнозначны, то локальные приоритеты критериев можно рассчитать как ЛПК = 1/количество критериев.
В нашей задаче критерии равнозначны, следовательно, нормализованный вектор локальных приоритетов будет иметь вид: 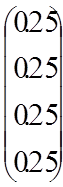
На пятом шаге рассчитываются глобальные приоритеты альтернатив. Для этого строится специальная вспомогательная матрица:
| Альтернативы | Критерий 1 | Критерий 2 | … | Критерий М |
| А1 | ЛПА11 | ЛПА12 | … | ЛПА1М |
| А2 | ЛПА21 | ЛПА22 | … | ЛПА1М |
| … | … | … | … | … |
| Аn | ЛПАn1 | ЛПАn2 | … | ЛПАnМ |
Где ЛПАij - локальный приоритет альтернативы Аi по критерию c номером j, полученный ранее при работе с матрицами попарных сравнений.
Для получения глобальных приоритетов альтернатив (ГПА) необходимо эту матрицу умножить на вектор приоритетов критериев:
ГПАi = ЛПАi1*ЛПК1 + ЛПАi2*ЛПК2 + … + ЛПАiМ*ЛПКМ
Результатом решения (наилучшей альтернативой) будет та, глобальный приоритет которой максимален.
Методика решения задачи на ЭВМ
При решении задачи будем использовать табличный процессор Excel. Порядок решения задачи следующий:
Шаг 1. Введите матрицу попарных сравнений для альтернатив по критерию «Материальные затраты». Параллельно с вводом матрицы рассчитайте локальные приоритеты альтернатив:
| A | B | C | D | E | F | |
| Материальные затраты | Раст-во | Жив-во | ЛПА по критерию 1 | Норм. ЛПА | ||
| =1/1870 | =1/2500 | |||||
| Раст-во | =1/1870 | =B3/D2 | =СРГЕОМ(C3:D3) | =E3/$E$5 | ||
| Жив-во | =1/2500 | =B4/C2 | =СРГЕОМ(C4:D4) | =E3/$E$5 | ||
| =СУММ(E3:E4) | =СУММ(F3:F4) |
Повторите ввод матрицы для каждого последующего критерия.
Шаг 2. Постройте матрицу для нахождения глобальных приоритетов альтернатив, занеся в нее информацию из матриц попарных сравнений:
| A | B | C | D | E | F | |
| 21[1] | Альт-вы | Мат. затр. | Затр. труда | Прибыль | Вн. потр. | ГПА |
| 0,25 | 0,25 | 0,25 | 0,25 | |||
| Раст-во | =F3 | … | … | … | =СУММПРОИЗВ($B$22:$E$22;B23:E23) | |
| Жив-во | =F4 | … | … | … | =СУММПРОИЗВ($B$22:$E$22;B24:E24) |
В ячейках F23:F24 находятся итоговые оценки альтернатив.
Задача 2. Планирование выпуска продукции
Постановка задачи. Предприятие выпускает три сорта продукции А, В и С. Необходимо определить оптимальное сочетание объемов выпуска продукции всех трех сортов, исходя из значений следующих критериев:
| № | Критерий | А | В | С |
| Затраты материалов, руб./ед. прод. | 1,20 | 1,10 | 0,90 | |
| Затраты труда, чел.-ч/ ед. прод. | 0,5 | 0,7 | 0,6 | |
| Затраты времени оборудования, маш. ч/ ед. прод. | 0,7 | |||
| Спрос на продукцию по результатам работы фокусной группы потребителей, % | ||||
| Объем заказов, тыс. ед. | ||||
| Цена реализаци, руб./ ед. прод. | 2,60 | 2,20 | 1,90 |
Критерии выбора считаются неравнозначными. Наиболее значимыми критериями являются затраты (всех видов) и цены реализации, менее значимыми – удовлетворение спросов и выполнение заказов.
Методика решения задачи
По аналогии с задачей 1 на первом шаге необходимо построить иерархию системы:








На втором шаге необходимо провести оценивание альтернатив по критериям, аналогично задаче 1. При этом параллельно можно вычислить локальные приоритеты альтернатив.
На третьем шаге необходимо рассчитать локальные приоритеты критериев. В задаче № 1 все критерии были равнозначными, поэтому их локальные приоритеты находились просто. В данном случае критерии имеют различное значение для выбора предприятия. Поэтому требуется сравнить их друг с другом.
Для этого можно построить матрицу попарных сравнений аналогичную той, которая строится для сравнения альтернатив по критериям. Но в этой матрице заголовком будет название цели, а по строкам и столбцам – названия критериев. Веса критериев неизвестны, поэтому в матрицу их можно не включать:
| Цель | Затраты материалов | Затраты труда | Затраты оборудования | Спрос | Договоры | Цены |
| Затраты материалов | ||||||
| Затраты труда | ||||||
| Затраты оборудования | ||||||
| Спрос | 1/5 | |||||
| Договоры | ||||||
| Цены |
Матрица заполняется на основании экспертных оценок сравнения. При этом сравниваются элементы (в данном случае - критерии) строк с элементами столбцов. Оценка выставляется по шкале от 1 до 9 – оценка «1» означает «равнозначно», оценка «9» - наиболее сильное превосходство. Для показания слабости альтернативы используются обратные оценки – ½, 1/3, ¼ и т.д.
Например, в постановке задачи сказано, что наибольшим приоритетом обладают критерии затрат и цен, значит, при сравнении критерия «Затраты материалов» с критерием «Спрос» мы можем поставить оценку 5 в клетку на их пересечении (см. таблицу). Тогда как логично следует, что критерий «Спрос» слабее критерия «Затраты материалов», следовательно на их пересечении необходимо поставить оценку 1/5 (см. таблицу).
Полностью заполненная матрица попарных сравнений критериев будет выглядеть так:
| Цель | Затраты материалов | Затраты труда | Затраты оборудования | Спрос | Договоры | Цены |
| Затраты материалов | ||||||
| Затраты труда | ||||||
| Затраты оборудования | ||||||
| Спрос | 1/5 | 1/5 | 1/5 | 1/5 | ||
| Договоры | 1/5 | 1/5 | 1/5 | 1/5 | ||
| Цены |
Обратите внимание, что матрица является зеркальной – элементы ниже главной диагонали являются обратными к элементам, находящимся выше главной диагонали.
По аналогии с альтернативами, для матрицы попарных сравнений критерие необходимо рассчитать локальные приоритеты критериев и, возможно, нормировать их.
На 4 шаге необходимо построить таблицу для расчета глобальных приоритетов. Она строится аналогично той, которая была построена в задаче 1. Нормированные глобальные приоритеты альтернатив будут показывать доли объема выпуска продукции по сортам.
Решение задачи на ЭВМ также можно провести с помощью пакета MS Excel.
[1] Номера строк могут меняться в зависимости от того, как в реальности будут размещены данные на рабочем листе