Лекция14.
Гармонический осциллятор
Классический осциллятор
Если классическая частица находится в упругой среде, то со стороны среды на неё действует сила, всегда направленная в сторону положения равновесия частицы и пропорциональная отклонению частицы от положения равновесия. Эту силу называют возвращающей. В результате частица совершает гармонические колебания, и поэтому её называют гармоническим осциллятором.
Простейшим осциллятором является одномерная частица. Так что сделаем первое приближение и будем считать осциллятор одномерным. Этот осциллятор совершает колебания только вдоль одной линии, потому естественно именно вдоль этой линии направить ось OX системы координат. Остальные оси нам не понадобятся. Начало координат естественно поместить в положении равновесия частицы.
| U (x) |
| x |
| E |
| –x 0 |
| x 0 |
.
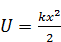Это – уравнение параболы.
Таким образом, классический одномерный гармонический осциллятор есть частица, совершающая колебания в параболической бесконечно глубокой потенциальной яме между точками с координатами x 0 и - x 0 (точками поворота), в которых полная энергия частицы E равна её потенциальной энергии:
.
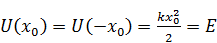Тот факт, что колебания частицы – гармонические, следует из второго закона Ньютона (дифференциального уравнения эволюции):
, 
.
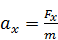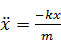Последнее уравнение можно переписать так:
, 
.
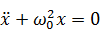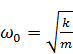Это есть дифференциальное уравнение гармонических колебаний. Его решение:
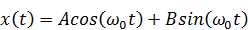или 
.
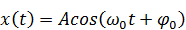Решение стационарного уравнения Шрёдингера.
А теперь выясним, как ведёт себя в этой яме микрочастица. Исследуем, в первую очередь, её стационарные состояния. Для этого запишем стационарное уравнение Шрёдингера (СУШ):
.
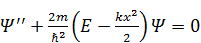Это – линейное однородное дифференциальное уравнение второго порядка. Плохо только, что оно не с постоянными коэффициентами. Как его решать? – Надо обратиться к учебникам или справочникам по математике. Но сначала попытаемся избавиться от параметров, входящих в это уравнение. Одним из способов, которым это можно сделать, является переход к безразмерной переменной. Введём новую переменную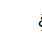 
, где b – некоторая константа, имеющая размерность длины. Новую переменную будем называть безразмерной координатой, а константу b подберём так, чтобы удалось максимально упростить дифференциальное уравнение.
Переход от x к ξ означает, что пси-функцию надо рассматривать теперь как Ψ (ξ), так что надо в дифференциальном уравнении перейти от дифференцирования по x перейти к дифференцированию по x, используя известное правило:
.
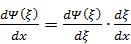Из этого правила следует:
, 
.
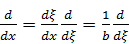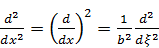В результате СУШ преобразуется так:
.
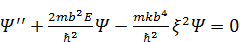Выберем константу b так, чтобы максимально упростить в этом уравнения третий член, который как раз и содержит непостоянный коэффициент. При этом учтём формулу для классической частоты колебаний осциллятора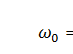 
.
Итак, приравняем коэффициент у третьего члена к единице:
⇒ 
.
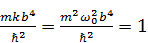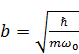Убедитесь самостоятельно, что константа b действительно имеет размерность длины. А теперь вернёмся к СУШ. Оно теперь стало короче:
.
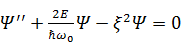Обратите внимание: величина 
имеет размерность энергии. Тогда можно от энергии E перейти к безразмерной энергии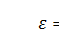 
, в результате чего СУШ ещё более упростится:
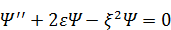. (1)
В этом уравнении остался единственный параметр – безразмерная энергия ε. Совсем исключить параметры, по-видимому, невозможно, ведь в исходное уравнение
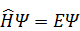
изначально входил параметр E (собственное число), от которого должно зависетьрешение уравнения (собственная функция ΨE).
Итак, у нас есть коротенькое дифференциальное уравнение, куда входит безразмерная переменная ξ и безразмерный параметр ε. Это, по-прежнему, линейное однородное ДУ с непостоянными коэффициентами, но зато с единственным параметром.Вот теперь можно обратиться к учебникам и справочникам по математике. Но мы ещё немного повременим – есть одна идея: не математическая, а физическа я.Так как частица находится в потенциальной яме, и яма эта – бесконечно глубокая, то состояние частицы безусловно связанное. Тогда пси-функция частицы должна в классически недоступной области (x > x 0 и x <- x 0) быстро убывать по мере удаления от точек поворота x 0 и - x 0. Можно предположить, что пси-функция есть произведение двух множителей
.
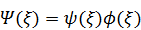Первый множитель ψ определяет поведение частицы в яме, второй множитель ϕ – за пределами ямы, то есть в классически недоступной области. Именно ϕ и определяет быстрое убывание пси-функции при x > x 0 и x <- x 0. Мы знаем, что в свободной области пси-функция убывает экспоненциально. Правда, свободные области слева и справа от ямы не совсем совпадают с классически недоступными областями, которые начинаются сразу за точками поворота. Однако весьма вероятно, не только в свободных областях, но и во всей классически недоступной области ϕ тоже имеет вид экспоненты. А так как яма симметричная, то и пси-поле должно быть симметричным, и описывающая его экспонента ϕ должна быть чётной функцией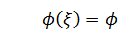 
. Например, это может быть такая функция:
.
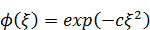Тогда
.
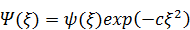Подставив эту функцию в СУШ и проделав некоторые преобразования, получим дифференциальное уравнение для множителя 
:
.
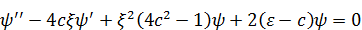Подходящим выбором константы c можно в этом уравнении избавиться от любого из его членов, кроме первого. Лучше всего избавиться от третьего члена – у него самый сложный коэффициент. Для этого надо положить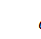 
. В результате получается такое уравнение:
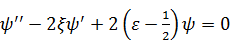. (2)
ДУосталось того же типа, что и (1) – линейное, однородное и с непостоянными коэффициентами. Вряд ли его можно назвать более простым, чем уравнение (1). Но у него есть одно важное достоинство: математики его знают, уже решали и знают решение. Это решение предложил известный французский математик 19 века Шарль Эрмит.
Энергетический спектр
Итак, благодаря Шарлю Эрмиту, решение уравнения (2) найдено.Однако мы должны быть уверены, что пси-функция 
удовлетворяет стандартным условиям, в частности, условию ограниченности. Пси-функция имеет вид:
.
Как мы предполагали, первый множитель определяет поведение пси-функции в яме, то есть в классически доступной области, а второй множитель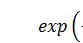 
определяет поведение пси-функции вне ямы, то естьв классически недоступной области.Второй множитель экспоненциально убывает до нуля,поэтому условие ограниченности, на первый взгляд, выполнятся. Но есть одна проблема. Надо, чтобы первый множитель в классически недоступной области вёл себя «хорошо».Лучше всего, если бы он по мере удаления от точек поворота убывал, а если он всё женарастает, то желательно, чтобы это нарастание было более медленным, чем убывание экспоненциального множителя, иначе условие ограниченности пси-функции нарушается.
Оказывается, что «хорошее» поведение 
наблюдается только в одном частном случае – когда входящая в дифференциальное уравнение (2) скобка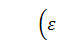 
– это целое числоn. При этом уравнение (2) имеет вид:
, 
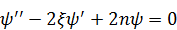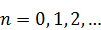(3)
Решение именно этого уравнения заинтересовало Эрмита. Он доказал, что решениемявляется полином степени n, причём множество этих полиномов для всевозможных n образует так называемую систему ортогональных функций. В его честь они были названы полиномами ЭрмитаHn (x).Что собой представляют полиномы Эрмита, мы рассмотрим в следующем параграфе. А здесь обратим внимание наусловие ограниченности пси-функции :
.
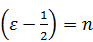Отсюда следует дискретность безразмерной энергии e:
.
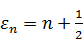Значит, и спектр энергии частицы E – тоже дискретный, и вот формула квантования энергии:
.
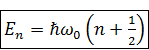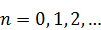
Целое число n, входящее в формулу квантования энергии, как вы уже знаете, принято называть главным квантовым числом.
Какие выводы можно сделать, анализируя эту формулу?
· Во-первых, минимальное значение n – не 1, как в задаче о частице в прямоугольной потенциальной яме, а нуль. Поэтому n – это не номер энергетического уровня, а номер возбуждённого уровня. Для основного состояния n = 0 и энергия основного состояния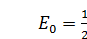 
.
· Во-вторых, энергетические уровни следуют друг за другом эквидистантно, то есть через равные интервалы.Каждый такой интервал – это минимальный квантэнергии, который равен . Этот квант получил специальное название – фонон. Любой другой квант энергии – это целое число фононов.
Понятие фонона обрело в физике твёрдого тела почти материальную оболочку. Дело в том, что удобной моделью твёрдого тела является упорядоченная в виде кристаллической решётки система независимых частиц-осцилляторов (атомов или ионов). Частицы расположены в узлах решётки, и для каждой из них окружающие её частицы выступают в двух ролях. Первая роль – коллективная: все вместе они создают упругую среду, в результате чего каждая из них становится гармоническим осциллятором, независимым от отдельных участников коллектива. Вторая роль – индивидуальная: каждый из осцилляторов время от времени вступает во взаимодействие со своими ближайшими соседями – в те случайные краткие момента времени, когда они подходят достаточно близко друг к другу (сталкиваются). Поэтому на языке квантовой физики поведение независимых осцилляторов твёрдого тела можно описать так.
Каждый из осцилляторов стремится занять своё основное стационарное состояние с энергией 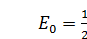, но вследствие хаотического соударения с соседними осцилляторами перескакивает на возбуждённые уровни. В результате такого прыжка энергия осциллятора изменяется на один или несколько фононов. Закон сохранения энергии требует, однако, чтобы увеличение энергии одного из сталкивающихся осцилляторов сопровождалось точно таким же уменьшением энергии второго осциллятора. Таким образом, каждая пара осцилляторов при столкновении друг с другом обменивается фононами. Но эту тему мы пока оставим – до следующего семестра, в котором нам предстоит изучать квантовую статистическую физику.