Задача синтеза систем автоматического регулирования (САР) является более сложной, чем задача анализа. При анализе автоматическая система задана. Пользуясь известными методами, необходимо оценить ее устойчивость, точность, качество переходного процесса. При синтезе указаны только основные требования, которым должна удовлетворять САР: точность, быстродействие, характер переходного процесса. Необходимо выбрать структуру автоматической системы и определить ее параметры, при которых были бы выполнены поставленные перед ней задачи. Как правило, задачу синтеза в большинстве случаев решают следующим образом.
На первом этапе с учетом требований к назначению системы и условий работы по каталогам серийного оборудования выбирают необходимые элементы системы: датчики, усилительно-преобразовательное устройство, исполнительное устройство. Систему, состоящую из объекта управления и выбранных элементов, будем называть исходной системой. Как правило, такая система либо неустойчива, либо устойчива, но не удовлетворяет поставленным требованиям к статическим и динамическим свойствам системы. Поэтому на втором этапе синтеза решают задачи обеспечения устойчивости и желаемого качества процесса управления, т.е. требуемой точности и качества переходного процесса. Для того чтобы этого добиться, есть два способа. Первый состоит в том, чтобы достигнуть этого путем изменения параметров данной системы, так как с изменением параметров меняются коэффициенты уравнений, а значит, и качество процесса. Если изменение параметров не позволяет получить желаемый результат, то надо применять второй способ — изменять структуру исходной системы, вводя дополнительные звенья, которые называются корректирующими устройствами (КУ) (другое название КУ – регуляторы).
|
|
Рассмотрим синтез САР на примере системы с последовательной коррекцией.
Пусть нам дан конкретный объект управления. Поставим цель управления: как можно точнее воспроизводить на выходе объекта сигнал задания g(t) и возможно полнее подавлять влияние возмущающего воздействия f(t) на выходную величину xp(t). Для этого мы замыкаем наш объект управления отрицательной обратной связью по величине xp(t). Как правило, в полученной автоматической системе нас может не устроить качество переходного процесса (рис. 2.6). В общем случае возможны два варианта: большие колебания в системе при большом быстродействии (кривая 1) и длительный переходный процесс при отсутствии колебаний (кривая 2). Очевидно, тот и другой варианты нам не подходят. Например, в механических системах, если регулируемой величиной является скорость, ее колебания могут вызвать значительные динамические нагрузки и, как следствие, выход механизма из строя. Большая длительность переходных процессов может привести к существенной потере производительности в тех случаях, когда время переходных процессов соизмеримо со временем основного рабочего цикла.
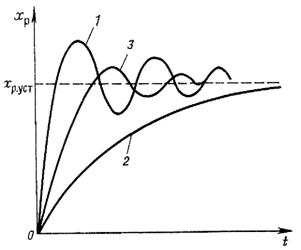
Рис.2.6. Варианты переходных процессов при синтезе системы автоматического
Регулирования
Решим следующую задачу: получить переходный процесс, который обладал бы достаточным быстродействием, но в то же время имел бы малое перерегулирование (кривая 3). Назовем такой переходный процесс оптимальным.
|
|
Включим в замкнутую САУ последовательно с объектом управления корректирующее устройство, которое назовем регулятором (рис. 2.7). Назовем операцию выбора передаточной функции регулятора с целью получения оптимального переходного процесса оптимизацией системы. Покажем решение этой задачи на конкретном примере.
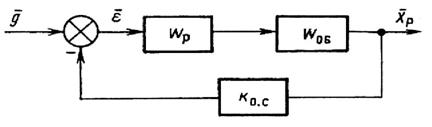
Рис. 2.7. Система автоматического управления с последовательной коррекцией
Пусть передаточная функция объекта Wоб представляет собой произведение двух инерционных звеньев:
W(p) =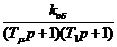 
. (2.8)
Причём постоянные времени Tm и T1 обладают следующим свойством: Tm << T1. Назовем постоянную времени Tm малой постоянной времени, а T1 — большой. Включим последовательно с объектом регулирования регулятор с передаточной функцией
W(p) =, (2.9)
где То.с и Tи — постоянные времени.
Назовем регулятор с такой передаточной функцией пропорционально-интегральным или ПИ-регулятором, так как его можно представить в виде параллельно включенных пропорционального и интегрального звеньев.
После включения регулятора передаточная функция прямой ветви контура регулирования
Wпр = Wоб Wp =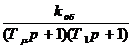 
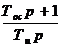, (2.10)
Выбирая значение постоянных времени ПИ-регулятора, можно изменять передаточную функцию прямой ветви регулирования. Пусть То.с=T1 и Tи=kо.сkобaTm, где а — коэффициент настройки регулятора. Тогда
Wпр =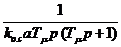 
. (2.11)
Отсюда видно, что путем подбора параметров передаточной функции ПИ-регулятора мы исключили влияние большой постоянной времени T1 в передаточной функции прямой ветви регулирования, ввели интегрирующее звено и оставили звено с малой постоянной времени. Исключение из передаточной функции Wпр(p) звена с большой постоянной времени, или, как говорят, «компенсация» большой постоянной времени, повышает быстродействие системы.
|
|
Пояснение. Мы провели чисто математическую операцию сокращения общих множителей в числителе и знаменателе выражения (2.10). После чего нами получено выражение (2.11). Реальные физические инерционные звенья из контура регулирования не исключаются. Полученный эффект «компенсации» постоянной времени обусловлен совместным действием регулятора и объекта управления, в результате чего переходный процесс в системе эквивалентен переходному процессу в случае отсутствия большой постоянной времени.
Покажем, что если передаточная функция прямой ветви регулирования имеет вид (2.11), то при замыкании объекта управления отрицательной обратной связью по регулируемой величине xp мы получим оптимальный переходный процесс. С этой целью найдем передаточную функцию замкнутой системы Wg по сигналу задания g. Ее значение равно (см. рис. 2.7):
Wg(p)=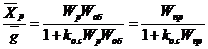 
. (2.12)
Подставляя в выражение (2.12) значение для передаточной функции прямой ветви, после преобразований получаем, что
Wg(p)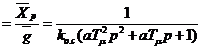 
. (2.13)
Полученная передаточная функция совпадает с передаточной функцией колебательного звена. Если мы будем менять коэффициент настройки регулятора а, то тем самым будут изменяться характер переходных процессов. На рис. 2.8 приведены графики переходных процессов при различных а для случая, когда сигнал задания равен единичной функции: g(t)=1(t). Их анализ позволяет сделать следующие выводы.
1. Колебательность системы регулирования определяется только коэффициентом а. Его подбором можно обеспечить требуемое качество переходных процессов.
2. Быстродействие ограничивается величиной малой постоянной времени Tm. Переходный процесс затухает в течение времени t= 6 Tm.
3. Величина коэффициента обратной связи kна переходный процесс не влияет. Это масштабный множитель, который определяет установившееся значение регулируемой величины xр уст.
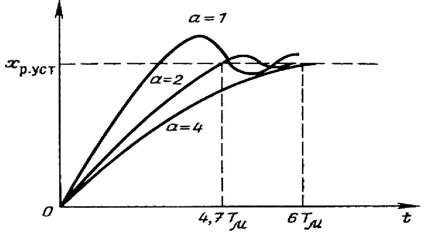
Рис. 2.8. Графики переходных процессов при различной настройке регулятора
Обычно при настройке регулятора принимается коэффициент a = 2. В этом случае время нарастания переходного процесса t= 4,7 Tm достаточно мало при практически пренебрежимом перерегулировании s = 4,3%. Такая настройка оптимальна для множества систем автоматического управления. Поэтому она используется в качестве основной стандартной настройки и называется настройкой на технический оптимум или оптимум по модулю.
Изложенное составляет основу широко используемого на практике метода синтеза САУ с последовательной коррекцией. Основная идея заключается в том, что, задавшись требуемым значением а и определив малую постоянную времени Tm, записывают желаемую передаточную функцию прямой ветви регулирования в виде (2.11), так как такая передаточная функция позволяет получить оптимальный переходный процесс. Отсюда можно найти передаточную функцию регулятора
Wр=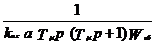 
. (2.14)
Однако, анализируя это выражение, не трудно убедиться, что передаточная функция регулятора по мере роста числа компенсируемых больших постоянных времени существенно усложняется. Например, если
Wоб=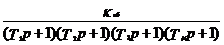 
,
то
W=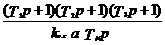 
.
Регулятор с такой передаточной функцией технически трудно реализовать. Если компенсировать только часть больших постоянных времени, то это приводит к снижению быстродействия системы автоматического управления. Поэтому если в контуре регулирования имеется больше двух подлежащих компенсации постоянных времени, то прибегают к введению подчиненных контуров регулирования.
Предположим, что объект управления имеет передаточную функцию Wоб, содержащую несколько больших постоянных времени. Кроме основной регулируемой величины xобъект управления характеризуется промежуточными координатами xp1,хp2,...,хpk. Введем отрицательные обратные связи по промежуточным координатам таким образом, чтобы объект регулирования был разбит на отдельные звенья:
Wоб = Wo1 Wo2...,Wok. (2.15)
Деление объекта управления на звенья должно осуществляться таким образом, чтобы каждое звено содержало только одну большую постоянную времени, подлежащую компенсации. Тогда для решения задачи оптимизации достаточно последовательно с этим звеном включить регулятор, который может быть легко реализован технически, и ввести вспомогательные контуры регулирования по промежуточным переменным так, как это показано на рис. 2.9.
Каждому звену объекта управления соответствуют своя регулируемая координата и свой регулятор. Регулятор внешнего контура регулирования вырабатывает сигнал задания для внутреннего контура регулирования. В такой системе управления внутренний контур подчинен задаче регулирования выходной величины внешнего контура. Поэтому данный принцип построения многоконтурной системы автоматического управления называется принципом подчиненного регулирования, а сами системы называются системами подчиненного регулирования координат.
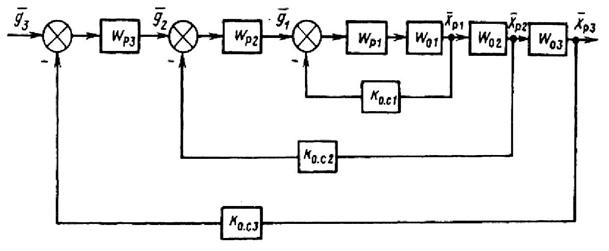Рис. 2.9. Структурная схема системы с подчиненным регулированием координат
Каждый контур регулирования оптимизируется раздельно, независимо от других. Оптимизация начинается с самого внутреннего контура. Самым последним оптимизируется контур, внешний по отношению ко всем контурам, который регулирует основную координату хp3. Выбор регуляторов осуществляется так же, как при последовательной коррекции. При разбивке объекта управления на звенья малая постоянная времени Tm всегда включается во внутреннее звено. Тогда после оптимизации для замкнутого контура 1 получим следующую передаточную функцию по задающему воздействию g1 [сравни с (2.13)]:
Wg1(p)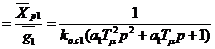 
. (2.16)
Выполненные расчеты и практика регулирования показывают, что при а³2, когда колебания демпфированы, без большой погрешности можно отбросить в выражении (2.16) р2 и полагать, что
Wg1(p)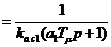 
.
Рассмотрим оптимизацию контура 2. Контур регулирования координаты хр2 включает в себя второе звено с большой постоянной времени и замкнутый контур 1. Следовательно, объект управления контура 2 имеет передаточную функцию:
Wо.к 2= Wо2Wg1 = Wо2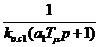 
.
Во втором контуре регулирования малая постоянная времени Тm2=a1Тm. Поэтому по аналогии с выражением (2.11) желаемая передаточная функция прямой ветви в контуре 2 имеет вид
Wпр2 = Wр2Wо.к2 =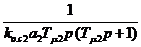 
.
Отсюда, так как передаточная функция Wо.к2 известна, найдем передаточную функцию регулятора Wр2. Передаточная функция замкнутого контура имеет вид
Wg2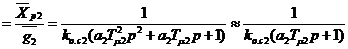 
.
Подобным образом рассчитывается и регулятор контура 3, вплоть до самого внешнего контура регулирования.
При настройке всех контуров на технический оптимум динамические процессы в них будут протекать аналогично — с небольшим перерегулированием (около 4,3%) и малой колебательностью. Однако в этом случае, если малая постоянная времени контура 1 равна Тm, то малая постоянная времени контура 2 составляет 2Тm, а контура 3 - 4Тm. Отсюда видно, что с увеличением числа контуров быстродействие уменьшается от внутреннего контура к внешнему. Это является недостатком систем с подчиненным регулированием координат. Для его устранения необходимо искать другие настройки контуров, лучшие по быстродействию, либо переходить к построению другой структуры системы автоматического регулирования.
Системы с подчиненным регулированием параметров нашли широкое распространение на практике, особенно при создании автоматизированных электроприводов. Это связано с их преимуществами по сравнению с другими системами:
независимой оптимизацией контуров регулирования, начиная с самого первого, что существенно упрощает как расчет, так и наладку системы в реальных условиях;
возможностью простыми средствами ограничивать по величине любую регулируемую координату. Для этого достаточно ограничить ее задание с помощью ограничения выходного сигнала соответствующего регулятора. В этом случае регулируемая координата не сможет превысить значения сигнала задания;
простотой реализации регуляторов вследствие их простых передаточных функций;
регуляторы могут быть реализованы на устройствах малой мощности, что позволяет применять датчики и устройства задания регулируемых координат с небольшим потреблением энергии.