Из данного ранее определения предела функции следует, что при значении x, очень близком к числу a, значение функции f (x) будет очень близко к пределу 
(конечно, если этот предел существует). Этим фактом можно воспользоваться, чтобы при помощи калькулятора найти приближённое значение предела, а потом, возможно, угадать, чему точно равен предел.
○ Пример 1. Найдём приближённое значение предела 
.
При x = 0,00001 имеем:
●
Точное значение этого предела:
(2)
где e = 2,718281828… (число e является основанием натурального логарифма: 
).
Равенство (2) называется второй замечательный предел.
○ Пример 2. Найдём приближённое значение предела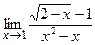 
и попытаемся угадать, чему равно его точное значение.
При x = 1,0001 имеем:
Можно предположить, что точное значение предела равно: – 0,5. В дальнейшем мы убедимся, что так оно и есть на самом деле. ●
Некоторые приёмы нахождения пределов.
Если функция f (x) определена в точке x = a, то, как правило, предел функции в этой точке равен значению функции в этой точке, то есть
.
○ Пример 3.
. ●
Пусть функция f (x) не определена в точке x = a, причем выражение f (a) имеет вид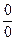 
. В этом случае принято говорить, что при вычислении предела 
мы имеем неопределённость вида 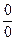. Чтобы найти предел, или, как принято говорить, раскрыть эту неопределённость, достаточно выражение f (x) путём тождéственных преобразований привести к такому виду g (x), чтобы значение g (a) уже существовало. Это значение и будет искóмым пределом.
○ Пример 4. Найдём предел 
.
Заметим, что при x = 3
.
То есть, мы столкнулись с неопределённостью вида 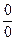. Чтобы её раскрыть, достаточно сократить дробь 
, предварительно разложив её числитель и знаменатель на множители, а затем подставить в полученное выражение x = 3:
. ●
Похожие задания на нахождение пределов из задачника Ермакова:
№№ 11.32, 11.33.
○ Пример 5. Найдём предел .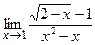
Заметим, что при x = 1
.
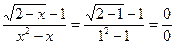То есть, мы столкнулись с неопределённостью вида 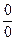. Чтобы её раскрыть, на этот раз нужно умножить числитель и знаменатель дроби на 
, или, как принято говорить, на выражение, сопряжённое к 
:
.
Заметим, что этот ответ мы ранее угадали при помощи калькулятора (см. пример 2). ●
По сути, смысл преобразований, проводимых при решении примеров 4 и 5, состоит в том, чтобы явно выделить в числителе и знаменателе исходной дроби множители, которые “ответственны” за появление неопределённости вида 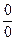, и сократить эти множители. После такого сокращения дробь уже определена в точке, в которой ищется предел.
Похожие задания на нахождение пределов из задачника Ермакова:
№№ 11.34(б), 11.41(б), 11.42(а).
Введение новой переменной при нахождении предела.
○ Пример 6. Найдём предел 
.
Мы снова сталкиваемся с неопределённостью вида .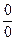
Иметь дело с корнями не очень-то приятно. Тем более, что здесь даже есть кубический корень.
Поэтому введём замену переменных: 
. Тогда
.
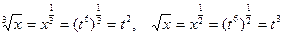Ещё заметим, что поскольку 
, то можно считать, что 
.
С учётом сделанных замечаний, искомый предел можно свести к новому, содержащему уже новую переменную t, и этот последний предел найти:
. ●
Похожие задания на нахождение пределов из задачника Ермакова:
№№ 11.34(а), 11.41(б).
№ 11.41(б): 
.
Введём новую переменную: 
. Тогда 
. Если 
, то 
. Поэтому
Ответ: 
.