Последовательностью называется бесконечный ряд чисел.
Например, такой:
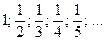(3)
Числа, образующие последовательность, называются членами последовательности.
Каждый член последовательности имеет порядковый номер (обозначающий номер места, на котором расположен этот член), а также обозначение: буква с индексом, указывающим порядковый номер члена.
Так для последовательности (3) имеем:
– первый член последовательности;
– второй член последовательности;
– третий член последовательности;
– четвёртый член последовательности;
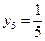– пятый член последовательности;
и так далее.
Вообще, член последовательности с номером n, или, как говорят, n - ый член последовательности (3), равен:
(4)
Равенство (4) называется формула n - го члена последовательности. По ней можно найти любой член, зная его номер. Или, наоборот, номер члена, если известен член последовательности.
○ Пример 13. Последовательность задана формулой n - го члена:
.
Тогда её сотый член равен
.
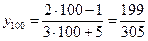Для того, чтобы найти номер члена, равного 
, нужно решить уравнение:
.
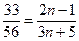В итоге получаем: n = 17. ●
Нетрудно видеть, что члены последовательности (3) всё ближе подходят (стремятся) к нулю по мере увеличения их номеров. Действительно, n -ый член этой последовательности равен 
, а значение этого выражения стремится к нулю по мере того, как натуральное число n неограниченно увеличивается.
В этом случае принято говорить, что последовательность имеет предел, равный нулю, при n стремящимся к бесконечности. Пишут:
.
Число b называется пределом последовательности, заданной формулой n - го члена 
, при n стремящимся к бесконечности, если при неограниченном возрастании натурального числа n значение выражения 
приближается к числу b.
При этом принято писать:
или
.
При нахождении предела последовательности, заданной формулой n - го члена , пользуются теми же приёмами, что и при нахождении предела функции, заданной формулой 
при 
.
○ Пример 14. Найдём предел последовательности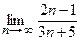 
. Для этого, как мы помним (см. пример 10), нужно числитель и знаменатель дроби поделить на n:
. ●
○ Пример 15. 
. ●
○ Пример 16. 
. ●
Пример 17. 
.
/здесь, очевидно: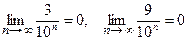 
/. ●
Так же, как в примерах 16 и 17, можно находить аналогичные пределы функции 
при .
Похожие задания на нахождение пределов из задачника Ермакова:
№№ 11.2-11.6, 11.8, 11.10-11.13, 11.38, 11.39.
Приложение.
Иллюстрация пределов по графикам
График функции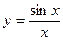 
По этому графику можно проиллюстрировать пределы:
По этому графику можно проиллюстрировать пределы: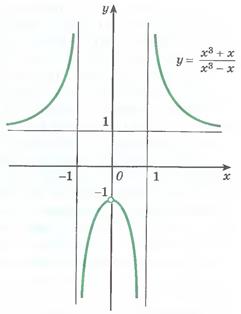 
Односторонние пределы
Число А 1 – это левый односторонний предел функции f (x) в точке x 0.
Число А 2 – это правый односторонний предел функции f (x) в точке x 0.
Число | А 1 – А 2 | – это скачок функции f (x) в точке x 0.
Обозначения:
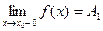, или коротко 
.
, или коротко 
.
Для левого и правого односторонних пределов в нуле используют обозначения: 
и 
.
Примеры.
Для функции, график которой изображён слева, имеем:
– левый односторонний предел в точке x = 4;
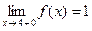– правый односторонний предел в точке x = 4;
значение функции в точке x = 4 равно f (4) = 1;
скачок функции в точке x = 4 равен |1 – 3| = 2.
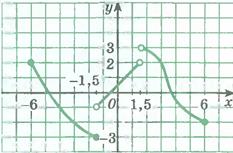Для функции, график которой изображён слева, имеем:
– левый односторонний предел в точке x = 1,5;
– правый односторонний предел в точке x = 1,5;
функция в точке x = 1,5 не определена;
скачок функции в точке x = 1,5 равен |2 – 3| = 1.
Для функции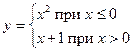 
имеем:
– левый односторонний предел в точке x = 0;
– правый односторонний предел в точке x = 0;
значение функции в точке x = 0 равно f (0) = 0;
скачок функции в точке x = 0 равен |0 – 1| = 1.
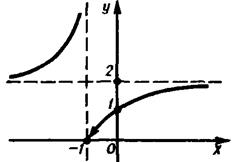Для функции 
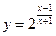имеем:
– левый односторонний предел в точке x = –1;
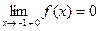– правый односторонний предел в точке x = –1;
функция в точке x = –1 не определена.
Кроме того функция имеет предел на бесконечности, равный
.
Задание для самостоятельной работы
Для функции 
(см. график внизу) найдите оба односторонних предела в точке x = 0 и предел на бесконечности.
Подтвердите свои наблюдения при помощи непосредственных вычислений этих пределов.