Задача линейного программирования

Применение математического моделирования к решению

Некоторых практических задач

Модель в широком смысле слова – это любой образ (мысленный или условный: изображение, описание, схема, чертеж, график, план, карта и т. п.) какого-либо объекта, процесса или явления, который используется в качестве его «заместителя», «представителя».

Математическая модель – это приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математического языка и математической символики.

Процесс математического моделирования, который сводит исследование реальных явлений к математическим задачам, занимает ведущее место среди других методов исследования, особенно с появлением компьютеров. Он позволяет проектировать новые технические средства, работающие в оптимальных режимах, решать сложные задачи науки и техники, проектировать новые явления. Это – мощный метод познания реальности, а также прогнозирования и управления, позволяющий проникнуть в сущность изучаемых процессов и явлений.

В настоящее время методы математического моделирования столь широко применяются в различных областях человеческой деятельности, что многие математики считают, что современную математику надо в первую очередь понимать как теорию математических моделей.

Процесс математического моделирования можно разбить на четыре этапа.

Первый этап – формулировка проблемы (задачи) и исследование свойств объекта моделирования. Этот этап завершается записью в математических терминах сформулированных качественных представлений об изучаемом объекте или явлении.

Второй этап – исследование математических задач, которые получены на первом этапе. Здесь основным вопросом является решение прямой задачи. На этом этапе важную роль приобретают математический аппарат и вычислительная техника. Здесь следует заметить, что одна и та же математическая модель может описывать свойства далеких друг от друга по своему конкретному содержанию реальных ситуаций. Примером может служить рассмотренная ниже основная задача линейного программирования. Это дает возможность исследовать возникающие таким образом математические задачи как самостоятельный объект, отвлекаясь от явлений, которые к ним привели.

Третий этап – выяснение того, насколько согласуется полученный математический результат со свойствами изучаемого реального объекта, процесса или явления.

Четвертый этап – корректировка (модернизация) модели в зависимости от глубины изучения моделируемых объектов

Простейшие задачи на построение математических моделей встречаются уже в школьной математике, например, при решении текстовых задач, построении чертежей в геометрии, эскизов графиков функций, использовании графов для решения вероятностных задач. Некоторые математические модели нами уже рассмотрены в предыдущих главах:

– использование кругов Эйлера (1.2.1);

– применение алгебры высказываний к исследованию функционирования контактных схем и их упрощению (2.2.3);

– решение практических задач с помощью составления логических уравнений и исследования формул логики на истинность (2.2.1);

– применение производных и интегралов к решению задач из сферы экономики и социологии (п. 3.3.3 и п. 3.4);

– матричная алгебра в экономике (4.2) и матричные модели в теории игр (4.3.);

– модели аксиоматических теорий.

В данной главе рассматриваются математические модели широко известных практических задач.

Задача линейного программирования

Задачей линейного программирования называют задачу отыскания оптимума (максимума или минимума) заданной линейной функции от нескольких переменных, если ее аргументы удовлетворяют системе линейных уравнений или неравенств. Математическая формулировка этой задачи выглядит следующим образом.

Найти наибольшее (наименьшее) значение функции , аргументы которой удовлетворяют системе ограничений:

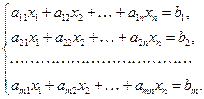
Здесь, коэффициенты 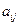, , 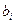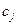– заданные числа, причем можно считать, что все числа . Кроме того, следует иметь в виду, что система ограничений помимо уравнений может содержать и неравенства и что переменные, как правило, удовлетворяют условиям 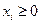, которые называются условиями неотрицательности.

Решение 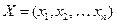системы ограничений, при котором функция цели 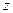достигает своего наибольшего (наименьшего) значения, называется оптимальным.

Задача линейного программирования является математической моделью многих практических задач экономического содержания. Некоторые из низ указаны на ниже приведенной схеме.

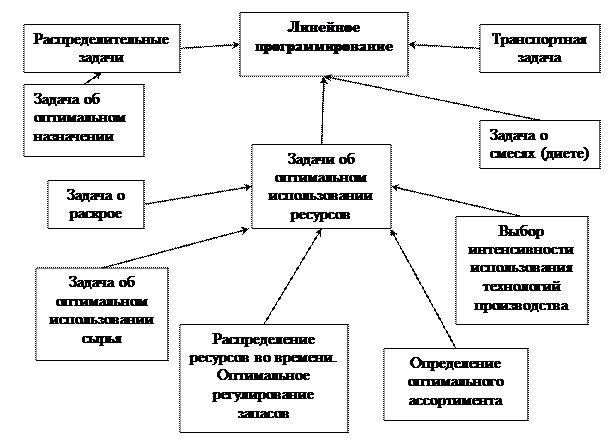Рассмотрим отдельные из них.