Пусть предприятие выпускает  различных изделий
различных изделий  . Для их производства требуется
. Для их производства требуется  различных видов ресурсов (разных видов сырья, вспомогательных материалов, людских ресурсов и т.д.). Эти ресурсы ограничены и составляют в планируемый период соответственно
различных видов ресурсов (разных видов сырья, вспомогательных материалов, людских ресурсов и т.д.). Эти ресурсы ограничены и составляют в планируемый период соответственно  условных единиц.
условных единиц.
Известны также технологические коэффициенты 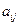 , которые показывают, сколько единиц
, которые показывают, сколько единиц  -го ресурса требуется для производства одной единицы изделия
-го ресурса требуется для производства одной единицы изделия  .
.
Пусть прибыль от реализации одной единицы изделия  равна
равна 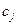 денежных единиц. В планируемый период все показатели
денежных единиц. В планируемый период все показатели 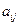 ,
, 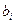 и
и 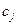 предполагаются постоянными.
предполагаются постоянными.
Составить такой план выпуска продукции, при котором прибыль предприятия от ее реализации была бы наибольшей.
Решение. Прежде чем составить математическую модель этой задачи, сведем все данные в таблицу:
| Виды ресурсов | Запасы ресурсов | Технологические коэффициенты | |||||

| 
| … | 
| … | 
| ||

| 
| 
| … | 
| … | 
| |

| 
| 
| … | 
| … | 
| |
| … | … | … | … | … | … | … | |
| i | 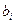
| 
| 
| … | 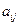
| … | 
|
| … | … | … | … | … | … | … | … |
| m | 
| 
| 
| … | 
| … | 
|
| Прибыль | 
| 
| … | 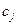
| … 
| 
| |
| Планируемый выпуск | 
| 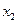
| … | 
| … | 
|
Составим ограничение на ресурсы. Использование  -го ресурса на изготовление всех видов изделий не должно превышать запас
-го ресурса на изготовление всех видов изделий не должно превышать запас 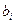 этого ресурса, поэтому получаем систему
этого ресурса, поэтому получаем систему

Из условия задачи ясно, что  ,
,  , …
, …  . Прибыль от реализации продукции выражается функцией
. Прибыль от реализации продукции выражается функцией  .
.
Требуется найти такие неотрицательные значения переменных 
 …,
…,  , при которых функция
, при которых функция  достигает наибольшего значения.
достигает наибольшего значения.
Заметим, что если использовать все имеющиеся запасы ресурсов, то неравенства в системе ограничений обращаются в равенства.
1. Для изготовления изделий №1 и №2 склад может отпустить металла не более 80 кг, причем на одно изделие №1 расходуется 2 кг, а на изделие №2 – 1кг металла. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий №1 требуется изготовить не более 30 шт., а изделий №2 – не более 40 шт., причем одно изделие №1 стоит 5 руб., а №2 –3 руб.
Решение. Составим математическую модель задачи. В качестве переменных здесь выступает план выпуска изделий. Пусть спланировано выпустить изделий №1  шт., а изделий №2 –
шт., а изделий №2 – 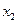 шт. По условию задачи
шт. По условию задачи 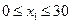 ,
,  . На изготовление всех изделий металла потребуется
. На изготовление всех изделий металла потребуется  кг. По условию запасы металла составляют 80 кг, поэтому должно выполняться условие
кг. По условию запасы металла составляют 80 кг, поэтому должно выполняться условие  . Прибыль от реализации всех изготовленных изделий составит
. Прибыль от реализации всех изготовленных изделий составит  рублей. Итак, получена математическая модель этой конкретной задачи.
рублей. Итак, получена математическая модель этой конкретной задачи.
Найти такие решения системы  при которых функция
при которых функция  принимает наибольшее значение. Для решения задачи используем графический метод. Для этого на координатной плоскости
принимает наибольшее значение. Для решения задачи используем графический метод. Для этого на координатной плоскости  изобразим множество точек, координаты которых удовлетворяют заданной системе неравенств (рис. 1). Решением системы является заштрихованный пятиугольник. В каждой точке плоскости
изобразим множество точек, координаты которых удовлетворяют заданной системе неравенств (рис. 1). Решением системы является заштрихованный пятиугольник. В каждой точке плоскости  функция
функция  принимает конкретное значение
принимает конкретное значение  . Множество точек, для которых
. Множество точек, для которых 
 , есть прямая линия, которая проходит перпендикулярно вектору
, есть прямая линия, которая проходит перпендикулярно вектору  . Рассмотрим прямую
. Рассмотрим прямую 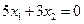 . Если эту прямую передвигать параллельно самой себе в направлении нормального вектора
. Если эту прямую передвигать параллельно самой себе в направлении нормального вектора  , то значения функции
, то значения функции 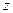 будут возрастать.
будут возрастать.
 Вершина, в которой прямая при движении в направлении вектора
Вершина, в которой прямая при движении в направлении вектора  впервые встретится с многоугольником решений, будет точкой, в которой функция цели принимает наименьшее значение. Последняя общая вершина движущейся прямой и многоугольника (точка выхода) – точкой, в которой функция цели принимает наибольше значение. В нашей задаче искомой точкой будет точка (20,40). В ней
впервые встретится с многоугольником решений, будет точкой, в которой функция цели принимает наименьшее значение. Последняя общая вершина движущейся прямой и многоугольника (точка выхода) – точкой, в которой функция цели принимает наибольше значение. В нашей задаче искомой точкой будет точка (20,40). В ней 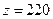 .
.
Таким образом, чтобы получить максимальную прибыль предприятие должно выпустить 20 изделий первого типа и 40 изделий второго типа. Прибыль при этом составит 220 рублей.
2. Производственная мощность цеха сборки составляет120 изделий типа 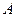 и 360 изделий типа
и 360 изделий типа  в сутки. Технический контроль пропускает в сутки 200 изделий того или другого типа (безразлично). Изделия типа
в сутки. Технический контроль пропускает в сутки 200 изделий того или другого типа (безразлично). Изделия типа 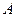 вчетверо дороже изделий типа
вчетверо дороже изделий типа  . Требуется спланировать выпуск готовой продукции так, чтобы предприятию была обеспечена максимальная прибыль от этого цеха.
. Требуется спланировать выпуск готовой продукции так, чтобы предприятию была обеспечена максимальная прибыль от этого цеха.
Решение. Пусть по планунадо выпустить  изделий типа
изделий типа 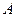 и
и 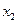 изделий типа
изделий типа  . По условию
. По условию  и
и 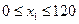 ,
,  . Получили систему ограничений. Пусть цена реализации одного изделия типа
. Получили систему ограничений. Пусть цена реализации одного изделия типа  составляет 1 ден. ед. Тогда для изделия типа
составляет 1 ден. ед. Тогда для изделия типа 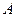 она составляет 4 ден. ед. Прибыль от реализации всех изготовленных по плану изделий составит в итоге
она составляет 4 ден. ед. Прибыль от реализации всех изготовленных по плану изделий составит в итоге  ден. ед. Требуется, чтобы значение
ден. ед. Требуется, чтобы значение 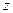 было максимальным. Получили задачу линейного программирования. Решите ее графически самостоятельно. (Ответ:
было максимальным. Получили задачу линейного программирования. Решите ее графически самостоятельно. (Ответ:  ).
).
3. Составить математическую модель следующей задачи.
Найти оптимальное распределениедвух видов механизмов, имеющихся в количествах  ,
,  между тремя участками работ, потребности которых соответственно равны
между тремя участками работ, потребности которых соответственно равны  ,
,  ,
,  при следующей матрице производительности каждого из механизмов на соответствующем участке работы:
при следующей матрице производительности каждого из механизмов на соответствующем участке работы: 
4. Для изготовления изделий №1 и №2 имеется 100 кг металла. На изготовление изделия №1 расходуется 2 кг, а на изделие №2 – 4 кг металла. Составить план производства, обеспечивающий наибольшую выручку от продажи изделий, если отпускная стоимость одного изделия №1 составляет 3 руб., а изделия №2 –2 руб., причем требуется изготовить изделий №1 не более 40 шт., а изделий №2 – не более 20 шт.
5. Производственная мощность завода позволяет производить за месяц 200 электродвигателей типа 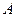 и 600 электродвигателей типа
и 600 электродвигателей типа  . Определите, сколько электродвигателей каждого типа должен производить завод для достижения максимальной прибыли, если: 1) двигатели обоих типов имеют одинаковую цену;
. Определите, сколько электродвигателей каждого типа должен производить завод для достижения максимальной прибыли, если: 1) двигатели обоих типов имеют одинаковую цену;
2) цена на двигатель типа 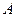 в три раза больше цены двигателя типа
в три раза больше цены двигателя типа  ;
;
3) цены на двигатели типов 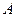 и
и  относятся как
относятся как  .
.
6. Автомобильный завод выпускает автомобили типов 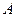 и
и  . Производственные мощности отдельных цехов или отделов приведены в следующей таблице:
. Производственные мощности отдельных цехов или отделов приведены в следующей таблице:
| Наименование цехов или участков | Количество машин за год | ||
Типа 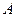
| Типа 
| ||
| Подготовка производства автомобилей Кузовной Производство шасси Производство двигателей Сборочный Участок испытаний | |||
Определите наиболее рентабельную производственную программу в следующих случаях: 1) прибыли от выпуска одной машины типов 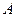 и
и  соответственно равны 200000 600000 рублей;
соответственно равны 200000 600000 рублей;
2) выпуск одной машины 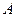 приносит прибыль в 2 раза меньшую, чем выпуск одной машины
приносит прибыль в 2 раза меньшую, чем выпуск одной машины  ;
;
3) в задаче1) производственная программа ограничена сверху условиями: машин типа 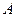 не более 50, а машин типа
не более 50, а машин типа  не более 60.
не более 60.
7. Из города 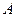 в город
в город  ежедневно отправляются пассажирские и скорые поезда. В таблице указаны наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные составы, и количество пассажиров, вмещающихся в каждый из вагонов:
ежедневно отправляются пассажирские и скорые поезда. В таблице указаны наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные составы, и количество пассажиров, вмещающихся в каждый из вагонов:
| Поезда | Вагоны | ||||
| багажный | почтовый | ж. плацк. | куп. | мягк. | |
| Скорый Пассажирский Число пассажиров Парк вагонов | – | – – |
Определите оптимальное число скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума.
8. Решите задачу 7, если пропускная способность дороги не позволяет в день пройти более, чем 6 пассажирским поездам.
Задачи о смесях
9. При составлении суточного рациона кормления скота можно использовать свежее сено (не более 50 кг) и силос (не более 85 кг). Рацион должен обладать определенной питательностью (число кормовых единиц не менее 30) и содержать следующие питательные вещества: белок (не менее 1 кг), кальций (не менее 100 г) и фосфор (не менее 80 г). В таблице приведены данные о содержании указанных компонентов в 1 кг каждого продукта питания и себестоимости (руб./кг) этих продуктов:
| Количество кормовых единиц | Белок г/кг | Кальций г/кг | Фосфор г/кг | Себестои- мость руб/кг | |
| Сено свежее Силос | 0,5 0,5 | 1,25 2,5 | 1,2 0,8 |
Определите оптимальный рацион из условия его минимальной стоимости
10. Составьте математическую модель следующей задачи.
Животноводческая ферма составляет рацион кормления коров на зиму. Имеются два научно разработанных рациона 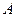 и
и  и произвольный рацион
и произвольный рацион  следующих составов:
следующих составов:
Рацион 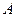
| Не менее 40% кукурузного силоса, не более 40% кормовых трав |
Рацион 
| Не менее 30% кукурузного силоса, не более 50% кормовых трав |
Рацион 
| Корм без ограничения |
Исходя из заготовок кормов, установлены следующие предельные нормы расхода каждого продукта: кукурузного силоса – 200 ц, кормовых трав – 300 ц. Какое количество каждого из рационов должна составить ферма, чтобы получить максимальную прибыль, если при рационе 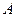 она составляет1000 руб./ц, при рационе
она составляет1000 руб./ц, при рационе  – 1200 руб./ц, а при рационе
– 1200 руб./ц, а при рационе  – 500 руб./ц?
– 500 руб./ц?
11. Для кормления подопытного животного ему необходимо давать ежедневно не менее 15 ед. химического вещества  (витамина или некоторой соли) и 15 ед. химического вещества
(витамина или некоторой соли) и 15 ед. химического вещества  . Не имея возможности давать эти вещества в чистом виде, можно приобретать вещество
. Не имея возможности давать эти вещества в чистом виде, можно приобретать вещество  по 10руб. или вещество
по 10руб. или вещество 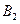 по 30 руб. за 1 кг. Каждый килограмм
по 30 руб. за 1 кг. Каждый килограмм  содержит 1 ед. вещества
содержит 1 ед. вещества  и 5 ед. вещества
и 5 ед. вещества  , а килограмм
, а килограмм 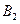 содержит 5 ед. вещества
содержит 5 ед. вещества  и 1 ед. вещества
и 1 ед. вещества  . Определите оптимальное содержание веществ
. Определите оптимальное содержание веществ  и
и 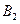 в ежедневном рационе.
в ежедневном рационе.
Задачи о раскрое
12. Для изготовлениябрусьев двух размеров: 0,6 м и 1 м в соотношении 2:1 на распил поступают бревна длиной в 2 м. Определить план распила, обеспечивающий максимальное число комплектов.
13. Составьте математическую модель следующей задачи.
Произвести распил 5-метровых бревен на брусья размерами 1,5; 2,4; и 3,2 м в отношении 2:3:5 так, чтобы минимизировать общую величину отходов.
14. Составьте математическую модель следующей задачи.
Полуфабрикаты поступают на предприятие в виде листов фанеры. Всего имеется две партии материала, причем первая партия содержит 400 листов, а вторая – 250 листов фанеры. Из поступающих листов фанеры необходимо изготовить комплекты, включающие 4 детали 1-ого типа, 3 детали 2-ого типа и 2 детали 3-его типа. Лист фанеры каждой партии может раскраиваться разными способами.
Количество деталей каждого типа, которое получается при раскрое одного листа соответствующей партии по тому или иному способу раскроя, представлено в следующей таблице.
| Первая партия | Вторая партия | |||||
  Детали Детали
| Способ рас пила | |||||
Требуется раскроить материал так, чтобы обеспечить изготовление максимального числа комплектов.