Как уже говорилось выше, несовместными событиями называют события, которые не могут произойти одновременно в одном опыте.
Суммой A+B двух событий называется событие, состоящее в появлении либо события A, либо события B, или обоих этих событий. Например, Если событие A - попадание снаряда в цель при первом выстреле, а событие B - попадание в цель при втором выстреле, то событие A+B - одно или два попадания в цель при двух выстрелах.
Если события A и B не совместные, то A+B - появление одного события, безразлично какого.
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей каждого события.
Докажем эту теорему на примере. В урне находится 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Вероятность появления цветного шара, очевидно 15/30. Вероятность появления красного шара 10/30, вероятность появления синего 5/30. События несовместные и

Определение суммы событий обобщается на любое число событий.
Полная группа событий.
Полную группу событий имеем тогда, когда нет возможных событий, не входящих в группу. Например, пара событий - появление цифры и появление герба при бросании монеты - является полной группой событий. Выпадение 1 очка, двух очков, 3-х, 4-х, 5- и 6 - очков - полная группа при бросании кости.
Теорема. Сумма вероятностей событий, образующих полную группу, равна единице, поскольку появление хотя бы одного события из полной группы - достоверное событие.
Противоположные события
Противоположными событиями называют два единственно возможных события, образующие полную группу. Например, попадание в мишень и промах - два противоположных события.
Теорема. Сумма вероятностей противоположных событий равна единице.
Пример. Вероятность того, что завтрашний день будет дождливым 0,3. Очевидно, вероятность ясного завтрашнего дня 1- 0,3 = 0,7.
Произведение событий.
Произведением AB двух событий называется событие, состоящее в одновременном появлении и события A, и события B.
Пример. Событие A - деталь годная (не бракованная), событие B - деталь окрашенная, событие AB - деталь годная и окрашенная.
Можно рассматривать произведение большего числа событий. Например, A - появление герба при бросании монеты, B - появление герба при повторном бросании монеты, C - появление герба при третьем подбрасывании монеты, ABC - появление герба при всех трех подбрасываниях монеты.
Условная вероятность.
Пусть имеются два (или более) события, одно из них зависит от другого. Пример. В урне 3 белых и три черных шара. Как узнать вероятность появления черного шара при втором вынимании, если при первом уже вынут черный шар? Задача может решаться "в лоб". Если при первом доставании вынут черный шар, то перед вторым доставанием возможных вариантов 5. Благоприятных из них - 2. Следовательно, вероятность события 2/5. Если обозначить событие A - первое доставание, а событие B - второе, то вероятность записывается как

Это обозначение условной вероятности.
Если считать событием A - появление при первом вынимании черного шара, а событие B - появление при повторном доставании такого же шара, то вероятность появления двух черных шаров при двух попытках определяется формулой

В нашем примере  Ясно, что
Ясно, что 
Эту же задачу можно решить, не используя указанную формулу. Рассуждаем следующим образом. Если производится два вынимания, то возможных исходов будет
 благоприятствующих исходов
благоприятствующих исходов 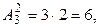 тогда
тогда 
Если A и B - независимые события, то есть происходят независимо друг от друга, то
 тогда
тогда