Мы уже познакомились с понятием случайной величины, некоторыми их свойствами, формулами, которые могут быть использованы в том, или ином случае для подсчета вероятности случайного события.
Выясним, какие случайные величины называются дискретными, а какие непрерывными? Для этого рассмотрим два примера.
Пример 1. Число родившихся мальчиков из ста новорожденных, конечно, случайная величина. Сколько же мальчиков может оказаться среди этих ста новорожденных? И один, и два, и 3, 4,………..100. Таким образом, случайная величина может принять одно из значений от 1 до 100. Ясно, что она не может принимать дробных значений. Если случайную величину считать функцией, то она меняется дискретно (через единицу)и является дискретной случайной величиной.
Пример 2. Расстояние, которое пролетает снаряд при выстреле в заданную цель также случайная величина, которая зависит не только от установки прицела, но и от силы и направления ветра, температуры воздуха, плотности порохового заряда и некоторых других параметров. В результате выстрела снаряд может попасть в цель, или отклониться на некоторое расстояние, причем любое в некотором промежутке. Как функция эта случайная величина изменяется непрерывно, то есть мы имеем дело с непрерывной случайной величиной.
Итак,
Дискретной называют случайную величину, которая принимает отдельные, изолированные значения с определенной вероятностью их появления. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
Непрерывной называется случайная величина, которая может принимать любые значения в некотором конечном или бесконечном промежутке. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Случайная величина (дискретная или непрерывная) может принимать значения с разной вероятностью. Поэтому для задания дискретной случайной величины недостаточно перечислить все ее значения, необходимо указать также вероятность появления каждого из них.
Законом распределения дискретной случайной величины (о непрерывных случайных величинах будет сказано позднее) называют соответствие между ее возможными значениями и вероятностью их появления.
Закон распределения СВ может задаваться таблицей, или графиком, представляющим многоугольник распределения. При его построении для дискретной случайной величины ее значения, как правило, откладываются по оси абсцисс, вероятность появления этого значения - по оси ординат, затем точки соединяются прямыми.
Пример.
Табличное задание закона распределения СВ:
Пусть Случайная величина обозначается X, принимаемые ею значения 
, их вероятности 
, тогда закон распределения имеет вид
Таблица 1.
| X | ||||
| p | 0,2 | 0,1 | 0,4 | 0,3 |
Графическое задание СВ
Построить многоугольник распределения для ДСВ:
Таблица 2
| X | ||||
| p | 0,1 | 0,3 | 0,4 | 0,2 |
Если принимаемые ДСВ значения образуют полную группу, то есть никакие другие невозможны, сумма вероятностей равна единице. В приведенных выше примерах значения случайных величин представляют полную группу.
Биномиальное распределение ДСВ.
Пусть производится n независимых испытаний, в каждом из которых событие A может произойти, а может не произойти. Вероятность наступления этого события p во всех испытаниях одинакова. Тогда вероятность не наступления события 
. В качестве дискретной случайной величины X примем число наступивших событий A. Очевидно, возможные значения X: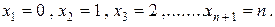 
Поскольку события независимые, для определения вероятности наступления каждого из них можно воспользоваться формулой Бернулли:
а 
число сочетаний из n элементов по k.
Если вспомнить формулу бинома Ньютона
то коэффициенты разложения бинома Ньютона совпадают с вероятностью соответствующего события в рассматриваемой задаче. Первый коэффициент разложения Ньютона определяет вероятность появления события A n раз, второй соответственно (n -1) раз и т.д. Последний коэффициент определяет вероятность того, что событие A не произойдет ни разу.
Пример. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого из элементов одинакова и равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Дискретная случайная величина X, дающая число отказавших элементов в одном опыте, принимает значения: 
и отражает безотказную работу или отказ одного, двух и трех элементов соответственно. Вероятность каждого события 
вероятность не наступления события, очевидно,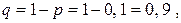 
тогда
Закон распределения ДСВ в этом примере задается таблицей 3
| X | ||||
| p | 0,729 | 0,243 | 0,027 | 0,001 |
Проверка: 0,729+ 0,243 + 0,027 + 0,001= 1,000.
Распределение Пуассона
Формула Бернулли удобна в случаях, когда число независимых испытаний n не очень велико, при больших n обычно используется формула Лапласа, но и она не удобна, если вероятность события мала. При большом количестве испытаний и малой вероятности p каждого из них используют формулу Пуассона если 
постоянная и конечная величина. В соответствии с ней вероятность наступления k событий в n испытаниях равна
Докажем эту формулу. В соответствии с формулой Бернулли, которую можно представить следующим образом
Если в полученной формуле перейти к пределу при 
, получим приближенное значение вероятности при больших n и конечных 
:
что и требовалось доказать.
Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность, что в момент транспортировки изделие придет в негодность 0,0002. Найти вероятность того, что на базу придут 3 негодных изделия.
Итак, n = 5000, p = 0,0002, k = 3, тогда 
По формуле Пуассона
Геометрическое распределение
Проводятся независимые испытания, в каждом из них вероятность наступления события равна p, а следовательно, вероятность не наступления 
Испытания проводятся до тех пор, пока не появится событие A. Обозначим за X число испытаний, которые необходимо провести, чтобы наступило событие A. Возможными значениями случайной величины X являются 
Пусть в первых 
событие A не наступило, появилось оно только в k - м испытании. Тогда по теореме умножения независимых событий имеем
.
Принимая k от 1 до бесконечности, получаем вероятности событий в виде геометрической прогрессии с начальным членом p и знаменателем прогрессии q:
По этой причине распределение называется геометрическим.
Пример. Из орудия стреляют до первого попадания в цель. Вероятность попадания 
Найти вероятность того, что цель будет поражена третьим выстрелом.
Числовые характеристики дискретной случайной величины.
Если закон распределения, который полностью характеризует случайную величину, не известен, используют другие сведения, дающие информацию о СВ. Это математическое ожидание, а также дисперсия или среднее квадратическое отклонение.
Математическое ожидание, его свойства.
Математическое ожидание приближенно равно среднему значению случайной величины. Иногда этого параметра достаточно для получения необходимой информации о случайной величине. Например, если среднее количество выбиваемых очков у одного из стрелков выше, чем у другого, можно сделать вывод, что первый стрелок - лучший из них.
Определение. Математическим ожиданием ДСВ называется сумма произведений значений случайной величины на вероятность ее появления:
Обоснуем эту формулу. Пусть произведено n испытаний, в которых случайная величина X приняла следующие значения: 
раз, 
раза,…. 
раз. Вычислим среднее значение этой случайной величины:
Ясно, что 
есть относительная частота появления события и формулу можно переписать следующим образом
Доказано, что относительная частота события при достаточно большом числе испытаний приближается к вероятности этого события. Таким образом,
Итак, математическое ожидание приближенно (при большом количестве испытаний) равно среднему значению случайной величины.
Если ДСВ принимает бесконечное количество значений, то
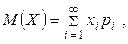
причем ряд должен сходиться абсолютно.
Замечание. Математическое ожидание ДСВ уже не является случайной величиной, а принимает определенное постоянное значение.
Пример найти математическое ожидание ДСВ, заданной таблицей 1.
Задание: Определить МО для СВ, задаваемых таблицами 2 и 3.
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:
Свойство 2. Постоянную величину можно вынести за знак математического ожидания:
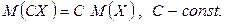
Оба эти свойства легко доказываются с помощью определения МО.
Свойство 3. Математическое ожидание произведения двух независимых событий равно произведению математических ожиданий этих событий:
.
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин:
.
Теорема. Математическое ожидание 
числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Доказательство. Очевидно, число появления события А во всех испытаниях равно сумме количеств появления события в каждом испытании. Но математическое ожидание суммы случайных величин равно сумме математических ожиданий (свойство 4). Поскольку испытания проводились в одинаковых условиях, математическое ожидание в каждом испытании равно вероятности появления события в этом испытании, и они равны:
Дисперсия, ее свойства.
Рассмотрим две случайные величины.
| X | - 0,01 | 0,01 |
| p | 0, 5 | 0, 5 |
| Y | - 50 | |
| p | 0, 5 | 0, 5 |
Ясно, что 
Если эти случайные величины представляют собой отклонение снаряда от цели, то первый же снаряд в первом случае поразит цель, а во втором случае она не будет поражена. Таким образом, математическое ожидание не всегда дает необходимую информацию. Необходимо как то учесть разброс значений. Для этого и вводится понятие дисперсии.
Рассмотрим закон распределения
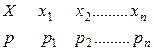
Запишем закон распределения отклонений случайной величины от ее МО. Вероятность отклонения случайной величины совпадает с вероятностью ее появления, так как МО - постоянная величина и на вероятность не влияет. Тогда
Теорема. Математическое ожидание отклонения случайной величины равно нулю.
Доказательство. Рассмотрим
Вышеприведенная цепочка рассуждений основана на том, что математическое ожидание суммы (разности) случайных величин равна сумме (разности) их математических ожиданий, и что МО постоянной равно самой постоянной. Отсюда следует, что бессмысленно оценивать разброс случайной величины, оценивая математическое ожидание отклонений, так как оно всегда будет равно нулю. Чтобы избавиться от этого недостатка, рассматривают квадраты отклонений.
Определение. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадратов ее отклонений:
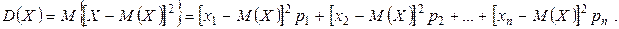
Пример. Рассмотрим закон распределения с таблицей 1. Математическое ожидание случайной величины подсчитано раньше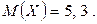 
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
Доказательство.
Проверим это на примере.
| X | ||||
| p | 0,2 | 0,1 | 0,4 | 0,3 |
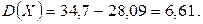
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. 
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
Свойство 4. Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность появления события p постоянна, равна произведению числа испытаний, вероятности появления события и вероятности непоявления события q = 1- p:
Среднее квадратическое отклонение.
Определение. Среднее квадратическе отклонение 
случайной величины X равно квадратному корню от дисперсии:
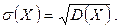
Среднее квадратическое отклонение рассмотренной выше случайной величины равно
Замечание. Дисперсия и среднее квадратическое отклонение так же, как и математическое ожидание, не являются случайными величинами, а имеют постоянное значение.
Теорема Чебышева.
Для попарно независимых случайных величин 
имеющих одно и то же математическое ожидание a, если дисперсии этих величин ограничены, вероятность неравенства
близка к единице, каким бы малым ни было 
Это означает, что среднее арифметическое случайных величин сколь угодно мало отличается от математического ожидания при достаточно большом n.
Теорема Бернулли.
Если в каждом из n независимых испытаний вероят н ость p появления события A постоянна, то как угодно близка к единице вероятность, того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико, то есть
где m - число появления события в n испытаниях.