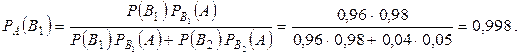Теорема. Вероятность появления хотя бы одного из событий 
, независимых в совокупности, равна разности между единицей и произведением вероятности противоположных событий 
Если A - появление хотя бы одного из событий , то событие A и событие 
(невозможность появления ни одного из событий ) единственно возможны, то есть образуют полную группу событий, вероятность которой равна 1. Тогда
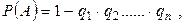
где 
вероятность события 
Пример. Произвели залп из трех орудий по одной цели. Пусть вероятность попадания в цель из первого орудия 
второго орудия 
третьего орудия 
Ясно, что эти события независимы. Тогда вероятность промаха из первого орудия 
из второго 
из третьего 
Следовательно, попадание в цель хотя бы одного снаряда в соответствии с вышеприведенной формулой
Формула полной вероятности.
Пусть событие A может наступить при условии появления одного из несовместных событий 
которые образуют полную группу событий. Известны вероятности этих событий 
и условные вероятности события A: 
. Вероятность события A определяется формулой
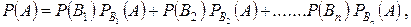
называемой формулой полной вероятности.
Пример. В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке - 10 деталей, из которых 9 стандартных. Из второй коробки вынута одна деталь и помещена в первую коробку. Найти вероятность того, что вынутая после этого из первой коробки деталь будет стандартной (событие A).
Решение. Из второй коробки могла быть извлечена стандартная (событие 
) и нестандартная (событие 
) деталь. Вероятности этих событий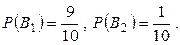 
Вероятность того, что из первой коробки будет извлечена стандартная деталь при условии, что из второй коробки переложили также стандартную деталь, 
Вероятность извлечения из первой коробки стандартной детали после перенесения в нее из второй коробки нестандартной детали 
Вероятность события A определяется по формуле полной вероятности 
Формулы Бейеса.
Пусть событие A может наступить при условии появления одного из несовместных событий которые образуют полную группу. Поскольку заранее не известно, какое из событий группы наступит, их называют гипотезами. Вероятность происхождения события A определяется формулой полной вероятности
Предположим, что произошло испытание, в результате которого произошло событие A. Возникает вопрос, как изменились вероятности гипотез после наступления события A? Для этого нужно подсчитать условные вероятности 
Вычислим сначала условную вероятность 
По теореме умножения имеем
Отсюда следует
Подставляя в полученную формулу выражение для 
, имеем одну из формул Бейеса
Весь набор формул Бейеса имеет вид
Пример. Известно, что 96% выпускаемой продукции удовлетворяет стандарту. Упрощенная схема проверки качества признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную - с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
Гипотезы: 
изделие стандартное, 
изделие нестандартное. Событие A - изделие признается пригодным. Очевидно,
Тогда
