Непрерывная случайная величина

Как уже говорилось выше, непрерывной случайной величиной называют случайную величину, которая может принимать любые значения на заданном интервале. Это не очень точное определение. Чтобы его уточнить рассмотрим случайную величину X, возможные значения которой сплошь заполняют интервал (a, b). Ясно, что перечислить все ее значения невозможно, а следовательно, нельзя ввести закон ее распределения по аналогии с дискретной случайной величиной.. Назовем вероятностью того, что случайная величина X примет значение, меньшее x, функцию F (x), тогда

и назовем ее функцией распределения вероятности. Теперь можно дать более точное определение непрерывной случайной величины.

Определение. Непрерывной случайной величиной называется величина, имеющая непрерывную функцию распределения с непрерывной производной.

 

Свойства функции распределения

Свойство 1. Значения функции распределения принадлежат отрезку [0, 1].

Это свойство непосредственно вытекает из определения вероятности случайного события, откуда следует, что вероятность - положительная величина, не превышающая единицу. Итак,

Свойство 2. Функция распределения есть неубывающая функция, то есть при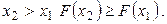

Доказательство. Чтобы случайная величина X принимала значение, меньшее , она должна находиться либо в интервале либо в интервале . Ясно, что эти два события несовместные, ибо случайная величина не может находиться и в том, и в другом интервале. Но вероятность суммы несовместных событий равна сумме их вероятностей

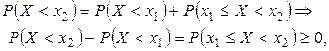
так как любая вероятность - неотрицательное число. Отсюда следует, что

Следствие 1. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.

Доказательство. Пусть 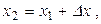тогда

Поскольку функция распределения - непрерывная функция, при 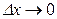эта разность также стремиться к нулю, следовательно, Тогда

 

 

Следствие 2. Вероятность того, что случайная величина примет значение в интервале (a, b) равна приращению функции распределения на этом интервале:

Пример. Случайная величина X задана функцией распределения

 

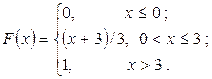
Найти вероятность попадания случайной величины в интервал (1; 2).

Решение:

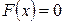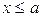Свойство 3. Если все возможные значения случайной величины принадлежат интервалу (a, b), то при , при

 

Плотность распределения

Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Ее можно задать и с помощью функции, называемой плотностью распределения.

Определение. Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (x) - первую производную от функции распределения F (x). Итак, 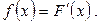Из определения функции распределения следует, что плотность распределения также непрерывная функция.

Теорема. Вероятность попадания непрерывной случайной величины X в интервал (a, b) равна определенному интегралу от плотности распределения, взятому в пределах от a до b:

Доказательство. Из формулы Ньютона-Лейбница следует

 

где Но что и требовалось доказать.

Пример. Задана плотность распределения вероятностей

 

Определить вероятность попадания случайной величины в интервал

Решение.

 

Свойства плотности распределения.

Свойство 1. Плотность распределения - неотрицательная функция. Это утверждение справедливо, поскольку функция распределения - неотрицательная функция, а следовательно, ее производная положительна.

Свойство 2. Несобственный интеграл от плотности распределения а интервале равен единице. Поскольку случайная величина обязательно попадет в указанный интервал, вероятность этого достоверного события, очевидно, равна единице.

 

Определение функции распределения по заданной плотности распределения.

 

Имеем

 

Вероятностный смысл плотности распределения

 

Вероятность того, что случайная величина примет значение из интервала с точностью до бесконечно малых высшего порядка по сравнению с равна произведению плотности вероятностей в точке x и длины интервала .

Доказательство:

 

Числовые характеристики непрерывных случайных величин.

 

Так же, как и для дискретных случайных величин, для непрерывных вводятся понятия математического ожидания, дисперсии, среднего квадратического отклонения.

Пусть непрерывная случайная величина X задана плотностью 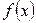и все ее значения принадлежат интервалу 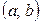. Разобьем этот интервал на n отрезков, длина каждого выберем на каждом из этих отрезков точку и подсчитаем сумму Поскольку вероятность попадания в интервал длиной равна , о чем только что говорилось выше, данная сумма, во-первых, представляет математическое ожидание как-бы дискретной случайной величины X, с другой стороны, представляет собой интегральную сумму Римана, а следовательно, ее предел при стремлении всех длин отрезков к нулю представляет собой определенный интеграл. Таким образом, математическое ожидание случайной величины равно

 

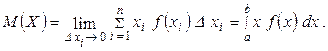
Определение 1. Математическое ожидание непрерывной случайной величины X, заданной плотностью 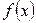, и все значения которой принадлежат интервалу 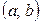вычисляется по формуле

 

Определение 2. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонений. При том же задании случайной величины

 

Учитывая, что математическое ожидание случайной величины постоянно, можно получить более простую формулу вычисления дисперсии. Итак,

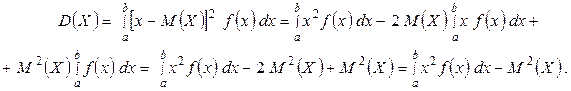
Таким образом,

Определение 3. Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для дискретной, соотношением

 

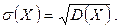
Пример. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной плотностью вероятностей

 

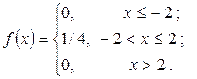
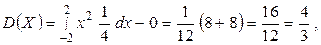
Примеры.

 

1.

 

2.

 

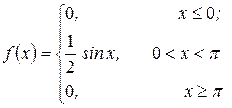
3.

 

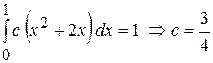
Законы распределения непрерывной случайной величины.

Равномерное распределение НСВ.

 

Это распределение задается следующим законом плотности распределения

 

 

Видим, что плотность распределения одинакова на интервале (a; b). Подсчитаем математическое ожидание, дисперсию и среднее квадратическое отклонение

 

 

Нормальное распределение вероятностей НСВ.

 

Нормальным называют распределение вероятностей НСВ, которое задается плотностью

 

Это распределение зависит от двух параметров. Определим их вероятностный смысл, для чего подсчитаем математическое ожидание и среднее квадратическое отклонение этой случайной величины.

 

 

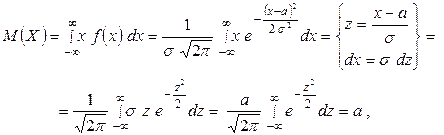
поскольку первый из интегралов равен нулю как интеграл от нечетной функции в указанных пределах, второй - интеграл Пуассона - равен 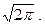Таким образом, первый параметр распределения - есть математическое ожидание.

Вычислим дисперсию по основной формуле

 

так как внеинтегральный член равен нулю, а интеграл - интеграл Пуассона.

Очевидно, второй параметр преобразования - есть среднее квадратическое отклонение.

График плотности вероятности для нормального закона распределения.

 

 

Вероятность попадания в заданный интервал нормальной СВ.

 

Имеем для интервала формулу:

,

из которой следует

 

Выразим полученный интеграл через функцию Лапласа

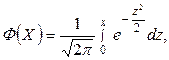
для которой имеются таблицы. Сделаем замену, которую использовали ранее

тогда

 

Вероятность заданного отклонения.

 

Если требуется вычислить вероятность отклонения случайной величины, заданной нормальным законом распределения, от ее математического ожидания на заданную величину используем только, что полученную формулу:

 

Требуется вычислить

 

в силу нечетности функции Лапласа. Итак,

 

Правило трех сигм.

 

Сделаем в только что полученной формуле замену тогда

При t =3 имеем Это означает, что вероятность того, что отклонение случайной величины, заданной нормальным законом, от ее математического ожидания, будет меньше , практически равна единице.

 

Задача 1. Математическое ожидание нормально распределенной случайной величины X равно a = 3 и среднее квадратическое отклонение Записать плотность вероятности X.

Задача 2. Нормально распределенная случайная величина X задана плотностью

Найти математическое ожидание и дисперсию.

Ответ. Математическое ожидание = 1, Дисперсия =

Задача 3. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X равно 10 и 2. Найти вероятность того, что в результате испытаний X примет значение в интервале (12, 14).

Задача 4. Производятся измерения диаметра вала без систематических (односторонних) ошибок. Случайные ошибки измерений X подчинены нормальному закону со средним квадратическим отклонением 10 мм. Найти вероятность того, что ошибки измерений не будут по абсолютной величине превосходить 15 мм.

Решение. Математическое ожидание ошибки равно нулю, тогда

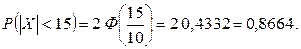
Задача 5. Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону, причем проектная величина детали 50 мм. Автомат выдает детали длиной, не меньшей, чем 32 мм, и не большей, чем 68 мм. Найти вероятность того, что выбранная наудачу деталь больше 55 мм.

Решение. Из соотношения имеем

Из таблицы имеем, что функция принимает значение 0,5 при откуда Теперь