Допустим, что пространство элементарных событий Ω состоит из конечного числа элементов:
Ω = 
.
Будем предполагать, что все события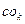 
, 
равновозможны. Построим алгебру событий S, включающую в себя:
1) невозможное событие Ø;
2) все , ;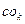
3) все события, представляемые в виде суммы любого количества событий из Ω.
Поскольку 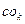, , равновозможны, а P (Ω) = 1, естественно принять P () =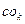 
.
Если теперь интересующее нас событие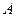 
является суммой m событий из Ω, т.е. событию 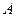благоприятствуют m событий из общего числа n, то вероятностью события 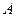естественно назвать отношение P () = 
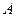. Итак,
Определение. Вероятностью события 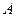называется отношение числа m исходов, благоприятствующих появлению события 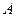к общему числу n исходов испытания:
P () = .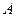
Рекомендуем читателю убедиться, что при таком определении все аксиомы
1) – 3) выполняются.
Приведём примеры решения задач с использованием классического определения вероятности.
Пример 2.1. Брошены две игральные кости. Какова вероятность того, что сумма очков, выпавших на их верхних гранях, будет не меньше трёх и не больше пяти?
Решение. Прежде всего, опишем пространство элементарных событий, связанных с данным испытанием. Элементами этого пространства являются события такого типа: какое-то число на верхней грани 1-ой кости и какое-то – на второй. На верхней грани каждой из костей может появиться любая из цифр то 1 до 6. Поскольку каждый исход на первой может сочетаться с каждым исходом на 2-ой, то интересующее нас пространство элементарных событий содержит 6 · 6 = 36 возможных исходов. Благоприятствующими интересующими нас событию являются следующие исходы:
| 1 кость | 2 кость | Сумма очков |
Всего этих исходов m = 9, поэтому вероятность искомого события (обозначим его через 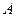) равна
P () =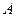 
.
Пример 2.2. В течение смены на телефонную станцию поступает 70 вызовов; 14 из них продолжительностью разговора более 10 минут. Какова вероятность
того, что случайно выбранный вызов имеет продолжительность разговора не более 10 минут?
Решение. Обозначим через 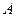– событие, что случайно выбранный вызов имеет продолжительность разговора не более 10 минут. Тогда 
- событие, что продолжительность этого разговора более 10 минут. Из 70 исходов испытания событию благоприятствуют 14 исходов. Поэтому
P () = 
Отсюда, используя свойство 
вероятности, получаем
P (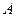) = 1- P () = 1 – 0,2 = 0,8
Для решения многих задач читателю рекомендуется вспомнить элементы комбинаторики.
Перестановками из n элементов называют комбинации из этих элементов, различающихся только порядком следования.
Число перестановок из n элементов вычисляется по формуле
= n!
Пример 2.3. Сколько различных телефонных номеров можно составить, если первой является цифра 2, а остальными – цифры 1, 3, 5, 6, 7, 8, каждая из которых не должна повторяться.
Решение. Поскольку первое место занято цифрой «2», то требуемых телефонных номеров можно составить столько, сколько существует перестановок из остальных шести цифр, т.е.
.
Размещениями из n элементов по m называются такие соединения по m элементов, которые отличаются одно от другого либо самими элементами, либо порядком их следования. Число всевозможных размещений из n элементов по m равно
.
Пример 2.4. Сигнал представляет собой упорядоченную пару флажков. Сколько сигналов можно составить, имея в наличии 7 флажков разных цветов?
Решение. Поскольку сигналы могут различаться как цветами флажков, так и порядком их следования, число сигналов равно числу размещений из 7 и 2
Сочетаниями из n элементов по m называются соединения по m элементов, отличающихся одно от другого хотя бы одним элементом.
Число сочетаний из n элементов по m 
определяется по формуле
.
Пример 2.5. Сколько есть способов составить делегацию из трёх студентов – отличников, если в группе всего 7 отличников.
Решение. Число таких способов равно количеству сочетаний из 7 по 3, т.е.
Пример 2.6. В группе 25 студентов, из которых 16 изучают английский язык. Случайно из группы выбирают 3-х студентов. Найти вероятность того, что все они изучают английский.
Решение. Всевозможных исходов испытания столько, сколько различных групп из 25 по 3 можно составить, т.е. n = 
. Благоприятных исходов m = 
. Поэтому, вероятность изучаемого события
P (A) = 
Пример 2.7. В ящике находятся 15 деталей, причём 10 из них имеют повышенное качество. Найти вероятность того, что из вытащенных наудачу пяти деталей три детали будут повышенного качества.
Решение. Опишем пространство элементарных событий, соответствующее испытанию (испытание – вытаскивание наудачу пяти деталей). Элементами этого пространства являются такие события – различные пятёрки деталей. Всего возможных исходов испытания столько, сколько различных комбинаций из 15 деталей по 5 можно составить. Это количество 
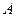. Обозначим через событие – среди вытащенных пяти деталей имеется точно три детали повышенного качества. Подсчитаем количество исходов, благоприятствующих появлению события 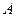. Так как детали повышенного качества можно выбирать только из деталей повышенного качества, то таких возможностей у нас 
. Каждая группа из 3-х деталей повышенного качества должна сочетаться с любой группой, состоящей из 2-х обыкновенных деталей, которых в нашем случае 
. Поэтому
.
И, следовательно, получаем
P (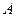) = 