Функция двух переменных (40 теста)
3.3.1.1/1
Значение функции двух переменных z=2х-y+15 в точке A(-2,1) равно
Ответ10
УС 1
Время 1
3.3.1.1/2
Значение функции двух переменных z=3х-2y+16 в точке A(1,2) равно
Ответ 15
УС 1
Время 1
3.3.1.2/1
П редел функциидвух переменныхz=х2+2y2+6 при 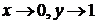 равен
равен
Ответ 8
УС 2
Время 1
3.3.1.2/2
П редел функциидвух переменныхz=х2-y2+5 при 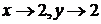 равен
равен
Ответ 5
УС 2
Время 1
Время 1
Время 1
3.3.1.3/1
Непрерывными функциями двух переменных в области  являются
являются
1). 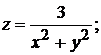 +2).
+2). 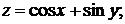 +3).
+3). 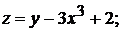 4).
4). 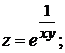
УС 3
Время 2
3.3.1.3/2
Непрерывными функциями двух переменных в области  являются
являются
+1). 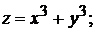 +2)
+2) 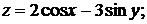 . 3).
. 3). 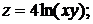 4).
4). 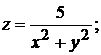
УС 3
Время 2
3.3.2.1/1
Частная производная 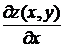 функции двух переменных
функции двух переменных 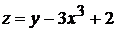 равна
равна
+1). 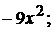 2).
2).  3).
3). 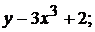 4).
4). 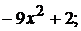 5). -3
5). -3
УС 3
Время 1
3.3.2.1/2
Частная производная 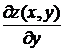 функции двух переменных
функции двух переменных 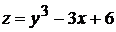 равна
равна
1). 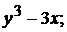 2) 6. 3).
2) 6. 3). 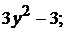 4).
4). 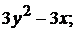 +5).
+5). 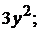
УС 3
Время 1
3.3.2.2/1
Частная производная 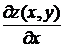 функции двух переменных
функции двух переменных 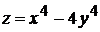 равна
равна
1). 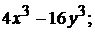 +2).
+2). 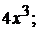 3).
3).  4).
4). 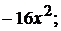 5). 4
5). 4
УС 3
Время 1
3.3.2.2/2
Частная производная 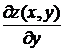 функции двух переменных
функции двух переменных 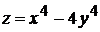 равна
равна
1). 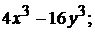 +2).
+2). 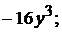 3).
3).  4).
4). 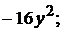 5). -16
5). -16
УС2
Время 1
3.3.2.3/1
Частная производная 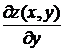 функции двух переменных
функции двух переменных 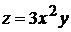 равна
равна
1). 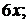 2).
2). 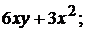 3). 6 4).
3). 6 4). 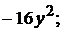 +5).
+5). 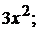
УС 3
Время 1
3.3.2.3/2
Для дифференцируемой в точке M(x,y) функции двух переменных z=f(x,y) верно:
1).В этой точке существует хотя бы частная производная 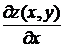
2).В этой точке существует хотя бы частная производная 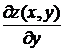
+3).В этой точке существует обе частные производные 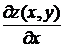 и
и 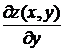
4).В этой точке не существует частных производных функции
УС 3
Время 1
3.3.2.4/1
Частная производная 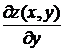 функции двух переменных
функции двух переменных 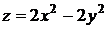 равна
равна
1). 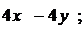 +2).
+2). 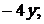 3).
3). 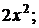 4).
4). 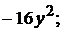 5). -4
5). -4
УС 2
Время 1
3.3.2.4/2
Частная производная 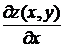 функции двух переменных
функции двух переменных 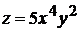 равна
равна
+1). 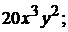 2).
2). 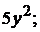 3).
3). 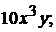 4).
4). 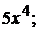 5). 20
5). 20
УС 3
Время 1
3.3.2.4/3
Частная производная 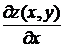 функции двух переменных
функции двух переменных 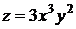 равна
равна
+1).  2). 3
2). 3 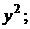 3).
3). 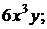 4).
4). 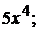 5). 20
5). 20
УС 3
Время 1
3.3.2.5/1
Полная производная сложной функции двух переменных 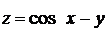 при
при 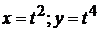 равна:
равна:
1). 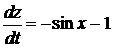 +2).
+2). 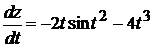 3).
3). 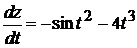 4).
4). 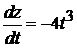 5). 1.
5). 1.
УС 3
Время 3
3.3.2.5/2
Полная производная сложной функции двух переменных 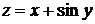 при
при 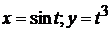 равна:
равна:
1). 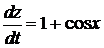 2).
2). 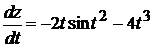 +3).
+3). 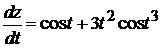 4).
4). 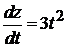 5). 1.
5). 1.
УС 3
Время 2
3.3.2.6/1
Дифференциал функции двух переменных 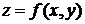 имеет вид:
имеет вид:
1). 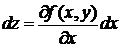 2).
2). 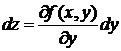
+3). 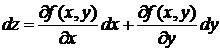 4).
4). 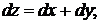
УС 3
Время 1
3.3.2.6/2
Дифференциал функции двух переменных 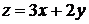 имеет вид:
имеет вид:
1). 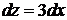 2).
2). 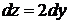 +3).
+3). 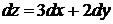 4).
4). 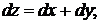
УС 3
Время 1
3.3.2.6/3
Дифференциал функции двух переменных 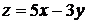 имеет вид:
имеет вид:
1). 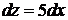 2).
2). 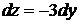 3).
3). 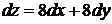 +4).
+4). 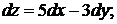
УС 3
Время 1
3.3.2.7/1
Касательная плоскость к поверхности 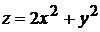 в точке М(1,1,3) равна:
в точке М(1,1,3) равна:
1). 2х+4y-z-3=0 +2). 4х+2y-z-3=0 3). 2х+2y+z+3=0
4). 2х+y+z-3=0 5). 4х+2y+3=0
УС 4
Время 3
3.3.2.7/2
Нормальный вектор касательной плоскости к поверхности 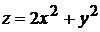 в точке М(1,1,3) равен:
в точке М(1,1,3) равен:
1). (4,2,0) 2). (4,2,1) +3). (4,2,-1) 4). (3,3,3)
5). (2,1,0)
УС 3
Время 3
3.3.2.7/3
Нормальный вектор касательной плоскости к поверхности 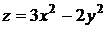 в точке
в точке
М(-1,1,1) равен:
+1). (6,-4,-1) 2). (3,2,0) +3). (3,-2,0) 4). (3,-2,-1)
УС 3
Время 3
3.3.2.8/1
Производная функции 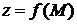 в точке М(х,у) по направлению вектора
в точке М(х,у) по направлению вектора 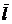 равна
равна
+1). 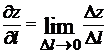 2).
2). 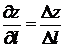 3).
3). 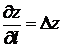 4).
4). 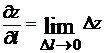
УС 3
Время 1
3.3.2.8/2
Производная функции 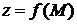 в точке М(х,у) по направлению единичного вектора
в точке М(х,у) по направлению единичного вектора 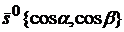 равна
равна
1). 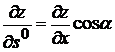 2).
2). 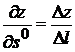 3).
3). 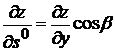
+4). 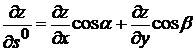 5).
5). 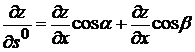
УС 4
Время 2
3.3.2.9/1
Градиент функции 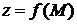 в точке М(х,у) равен
в точке М(х,у) равен
1). 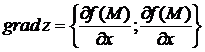 2).
2). 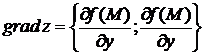 +3).
+3). 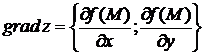 4).
4). 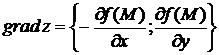
5) 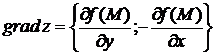
УС 3
Время 2
3.3.2.9/2
Градиент функции 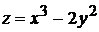 в точке М(1,2) равен
в точке М(1,2) равен
+1). grad z=(3,-8) 2).. grad z=(-8,3) 3).. grad z=(-3,8)
4).. grad z=(3,3) 5).. grad z=(-8,-8)
УС 3
Время 2
3.3.2.9/3
Градиент функции 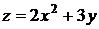 в точке М(2,-4) равен
в точке М(2,-4) равен
1). grad z=(2,-4) +2).. grad z=(8,3) 3).. grad z=(8,-12)
4).. grad z=(2,2) 5).. grad z=(-8,-8)
УС 3
Время 2
3.3.2.9/4
Градиент функции 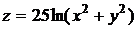 в точке М(3,-4) равен
в точке М(3,-4) равен
1). grad z=(25,25) 2).. grad z=(1,0) 3).. grad z=(8,-12)
4).. grad z=(2,2) +5).. grad z=(6,8)
УС 4
Время 3
3.3.2.9/4
Производная функции 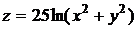 в точке М(3,-4) в направлении ее градиента равна
в точке М(3,-4) в направлении ее градиента равна
+1). 10 2).2 +3).0 4) 3
УС 5
Время 3
3.3.2.10/1
Частная производная второго порядка 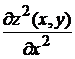 функции двух переменных
функции двух переменных 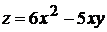 равна
равна
1). 6 +2). 12 3). 12-5ху 4). 12-5у
УС 3
Время 2
3.3.2.10/2
Частная производная второго порядка 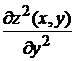 функции двух переменных
функции двух переменных 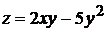 равна
равна
1). 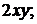 2).
2). 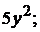 +3). -10 4).
+3). -10 4). 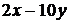
УС 3
Время 2
3.3.2.10/3
Частная производная второго порядка 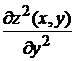 функции двух переменных
функции двух переменных 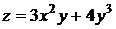 равна
равна
1).  2).
2). 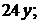 +3). 24 4).
+3). 24 4). 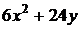
УС 3
Время 2
3.3.2.11/1
Частная производная второго порядка 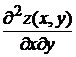 функции двух переменных
функции двух переменных 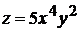 равна
равна
+1). 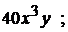 2).
2). 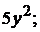 3).
3). 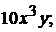 4).
4). 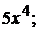 5). 40
5). 40
УС 3
Время 2
3.3.2.11/2
Частная производная второго порядка 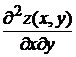 функции двух переменных
функции двух переменных 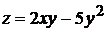 равна
равна
1). 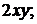 2).
2). 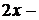
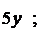 3).
3). 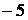 +4). 2
+4). 2
УС 3
Время 1
3.3.2.12/1
Функция двух переменных z=2x2 +2y 2 в точке (0,0) имеет
+1) экстремум 2). максимум +3). минимум 4). разрыв второго рода
УС 3
Время 2
УС 3
3.3.2.12/2
Функция двух переменных z=-4x2- - 6y 2 в точке (0,0) имеет
+1) экстремум +2). максимум 3). минимум 4). разрыв первого рода
УС 3
Время 2
УС 3
3.3.2.12/3
Минимум функции двух переменных z=128ху 2 (1-х-у) равен
Ответ 2
УС 5
Время 3
3.3.2.12/4
Максимум функции двух переменных z=x3- + y 3 -15ху равен
Ответ -125
УС 5
Время 3
3.3.2.12/5
Максимум функции двух переменных 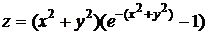 равен
равен
Ответ 0
УС 5
Время 3