Лекция 7. Цифровые фильтры
1. Определение и классификация ЦФ.
2. Основные этапы проектирования ЦФ.
3. Требования к АЧХ.
4. КИХ-фильтры с линейной ФЧХ.
5. Четыре типа КИХ-фильтров с ЛФЧХ.
6. Прямая приведенная структура КИХ-фильтра.
Определение и классификация ЦФ
Цифровым фильтром (ЦФ) называют ЛДС, выполняющую преобразование входной последовательности в выходную по алгоритму, описываемому РУ, который отображается заданной структурой, реализованной программно или аппаратно.
В узком смысле под ЦФ подразумевают частотно-избирательный ЦФ, предназначенный для ______________________________________________________
По типу избирательности различают_______________________________________
По типу ЛДС различают__________________________________________________
Основные этапы проектирования ЦФ
Основные этапы проектирования ЦФ:
1. ____________________________________
2. Выбор типа ЦФ (____________________)
3. Выбор метода синтеза.
4. Синтез ЦФ — расчет _________________________
5. Выбор ___________ ЦФ.
6. Компьютерное моделирование структуры ЦФ с учетом конечной разрядности данных.
7. Реализация структуры ЦФ на сигнальном процессоре (программная) или ПЛИС (аппаратная).
Требования к АЧХ
На рис. 7.1 представлены для ФНЧ: идеальная АЧХ (нормированная), требования к АЧХ и требования к характеристике затухания.
Рис. 7.1. Идеальная АЧХ ФНЧ; требования к АЧХ и
характеристике затухания
Требования к АЧХ задаются в основной полосе частот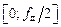 
и включают в себя:
□ ______________________________________
□ ____________________________________________________________________
□ ____________________________________________________________________
Характеристикой затухания называют АЧХ в децибелах:
(дБ). (7.1)
Вместо значений безразмерных 
, 
задаются их значения в децибелах:
□ 
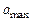(дБ) — максимально допустимое затухание в ПП;
□ 
(дБ) — минимально допустимое затухание в ПЗ.
На рис. 7.2—7.4 изображены идеальные АЧХ ФВЧ, ПФ и РФ и требования к АЧХ.
Рис. 7.2. Идеальная АЧХ ФВЧ и требования к АЧХ
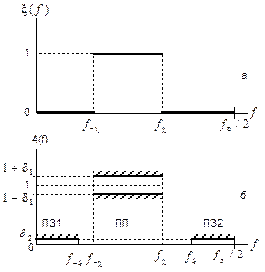
Рис. 7.3. Идеальная АЧХ ПФ и требования к АЧХ
Рис. 7.4. Идеальная АЧХ РФ и требования к АЧХ
КИХ-фильтры с линейной ФЧХ
Условие линейности ФЧХ (ЛФЧХ):
КИХ-фильтр с передаточной функцией
(7.2)
обладает строго линейной ФЧХ (с точностью до скачков на 
), если для его ИХ 
выполняется одно из двух условий:
· __________________
· __________________
.
Скачки ЛФЧХ на наблюдаются в точках __________________
Длина КИХ-фильтра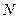 
равна длине ИХ.
Порядок КИХ-фильтра 
равен порядку _______________________________
.
Ось симметрии (антисимметрии) ИХ — в точке 
Четыре типа КИХ-фильтров с ЛФЧХ
Различают 4 типа КИХ-фильтров с ЛФЧХ по следующим двум признакам:
· ____________________________________ ;
· ____________________________________ .
Рассмотрим на примерах, результаты обобщим.
Для каждого типа КИХ-фильтра:
1. Запишем передаточную функцию.
2. Определим значение АЧХ на границах основной полосы 
.
3. Установим возможные типы избирательности ЦФ.
КИХ-фильтры типа 1 — порядок — четный R = 4, — симметричная:
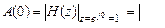
Вывод: КИХ-фильтры типа 1 могут использоваться для синтеза ______________
КИХ-фильтры типа 2 — порядок — нечетный R = 3, — симметричная:
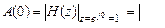
Вывод: КИХ-фильтры типа 2 могут использоваться для синтеза ______________
КИХ-фильтры типа 3 — порядок — четный R = 4, — антисимметричная:
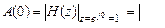
Вывод: КИХ-фильтры типа 3 могут использоваться для синтеза __________
КИХ-фильтры типа 4 — порядок — нечетный R = 3, — антисимметричная:
;
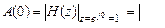
Вывод: КИХ-фильтры типа 4 могут использоваться для синтеза __________________
На стр. 6 приведена сводная таблица 4-х типов КИХ-фильтров.
Прямая приведенная структура КИХ-фильтра
Прямая приведенная структура используется для КИХ-фильтров с ЛФЧХ.
Пример 7.1. Изобразить прямую приведенную структуру КИХ-фильтра типа 1 длины 
.
Передаточная функция с учетом симметрии ИХ:
.
Приведем подобные слагаемые (отсюда название структуры — приведенная):
.
Прямая приведенная структура отображает алгоритм вычисления реакции по РУ:
Рис. 7.5. Прямая приведенная структура КИХ-фильтра 1-го типа длины N = 7
В прямой приведенной структуре число умножителей __________________________
| ИХ h (n) | Тип КИХ | Порядок R | Амплитудная функция 
Порядок полинома M
| ФЧХ | Тип избир-ти |
| Симметричная | Четный |  
| 
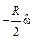
| ФНЧ ФВЧ ПФ РФ | |
| Нечетный |  
|
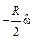
| ФНЧ ПФ | ||
| Антисимметричная | Четный | 
| 
| ПФ | |
| Нечетный |
|
| ПФ ФВЧ |