УНИВЕРСИТЕТ»
| Оценка: ________________ «___» ____________ 2014 г. | Кафедра Высшей математики и программного обеспечения ЭВМ |
Пояснительная записка к курсовой работе
«Решение краевой задачи для одного из уравнений математической физики»
по дисциплине «Специальные разделы высшей математики»
Выполнила:
студентка группы Ивт(б)-221
Пархимович Е.В.
Проверила:
доцент кафедры
ВМ и ПО ЭВМ
Кацуба В.С.
Мурманск
Оглавление:
1. Формулировка физической задачи. Задание на исследование…………………….….3
2. Решение задачи…………………………………………………………………………..4
2.1. Вывод уравнения состояния………………………………………………………4
2.2. Математическая модель…………………………………………………………...8
2.3. Решение модифицированным методом Фурье………………………………....10
2.4. Доказательство достоверности решения, полученного методом Фурье……...16
2.5. Численная реализация решения…………………………………………………18
2.6. Исследование решения…………………………………………………..………21
Заключение по работе…………………………………………………………………….…24
Список использованной литературы и прикладных пакетов программ (ППП)…...……25
Формулировка физической задачи. Задание на исследование
Дан тонкий однородный стержень длиной l, теплоизолированный по боковой поверхности, начальная температура которого равна 0. На конце x=l температура поддерживается равной нулю, а на конце x=0 она растёт линейно со временем так, что U(0,t)=At, где А - некоторая постоянная. Исследовать распределение температуры вдоль стержня в любой момент времени t>0.
(Задача 10(II; 127))
Задание на исследование:
При А=1 и l=1, материал стержня – дерево, выявить зону краевого эффекта от x=l и t=0.
Решение задачи
Вывод уравнения состояния
В ходе решения данной физической задачи необходимо исследовать распространение тепла в неравномерно нагретом твердом теле.
Рассмотрим вывод уравнения состояния в общем случае для тела, занимающего некоторый объем в пространстве XOYZ. Процесс распространения тепла будет характеризоваться функцией T (t,x,y,z), где t – время от начала процесса, (x,y,z) – декартовы координаты точек физического тела. Функция T (t,x,y,z) называется функцией состояния процесса.
Сформулируем следующую физическую модель процесса теплопроводности:
1) Происходит механический перенос тепла из мест с более высокой температурой в места с более низкой;
2) Все переносимое тепло идет на изменение температуры тела;
3) Внутри физического тела не исключается наличие истоков или стоков тепла;
4) Физические и теплофизические свойства материала, из которого изготовлено тело, считаются независящими от температуры, что обеспечивается не очень большим изменением температуры внутри тела.
5) Материал, из которого изготовлено тело считается однородным.
Из физики известен закон механического переноса тепла.
Закон теплопроводности (Закон Фурье):
Количество тепла, проходящего через некоторую площадку за малый промежуток времени, пропорционально произведению площади на длину промежутка времени и пропорционально производной функции температуры по нормали к этой площадке.
∆Q = -k ∙ ∆S ∙ ∆t ∙∂T/∂n -, где k – коэффициент теплопроводности.
Знак “-” объясняется тем, что перенос тепла осуществляется из мест с более с более высокой температурой в места с более низкой, т.е. по направлению нормали –n, составляющей тупой угол с направлением 
(направлением наибольшего возрастания температуры).
По свойствам градиента известно, что ∂T/∂n – это есть проекция вектора градиента T на направление n.
Если направление n брать единичным, то
,
где 
– оператор «набла».
– это чаще всего встречающаяся запись Закона Фурье.
Так как в рассматриваемом процессе все переносимое тепло с учетом источников и стоков должно уходить на изменение температуры тела, то нужно составить уравнение теплового баланса для любой конечной части объема, занятого физическим телом.
Уравнение теплового баланса для (V) за промежуток ∆t: Q1+Q2=Q3, где Q1 – это количество тепла, поступившее в объем (V) извне через его поверхность (S); Q2 - количество тепла, поступившее в объем (V) за счет работы внутренних источников и стоков; Q3 - количество тепла, ушедшего на изменение температуры в объеме (V).
Составляем формулы для Q1, Q2, Q3:
– поверхностный интеграл по (S) в направлении внутренней нормали.
Количество тепла Q2 можно описать введением функции f (x, y, z, t), которая характеризует плотность распределения источников, то есть количество тепла, которое выделяется в точке (x, y, z) за единицу времени.
Для составления величины Q3 используем еще один закон из физики – закон теплоемкости.
Закон теплоемкости:
На изменение температуры ∆T в малом объеме ∆V за время ∆t нужно затратить количество тепла ∆Q, пропорциональное изменению температуры и массе элемента объема ∆V.
где С – коэффициент теплоемкости материала, ρ – плотность материала, из которого изготовлено тело.
Обработка: ∆T = ∂T/∂t ∙∆t (c точки зрения математики, это есть замена малого приращения функции на ее дифференциал)
Записываем уравнение теплового баланса:
(1)
Чтобы от этого уравнения теплового баланса, составленного в интегральной форме, перейти к дифференциальной форме уравнения состояния, нужно использовать одно из легко доказываемых свойств различных интегралов:
1) для определенного интеграла:
если 
для Ɐ промежутка [a, b] и при этом f (x) является непрерывной, то f (x) = 0.
2) для двойного интеграла:
если 
для любой области D принадлежащей пространству R2 и f(x, y) непрерывна, то f (x, y) = 0.
3) для тройного интеграла:
если 
для любого объема V принадлежащего пространству R3 и f (x, y, z) непрерывна при 
то f (x, y, z) = 0 при 
Чтобы это свойство применить к равенству (1), в котором объем (V) – это любой конечный объем, выделенный в физическом теле, в котором идет процесс теплопроводности, необходимо воспользоваться формулой Остроградского-Гаусса.
Формула Остроградского-Гаусса (связь двойного интеграла по поверхности с тройным по объему):
Применяя эту формулу к поверхностному интегралу в равенстве (1) получим:
Подставляем это выражение в формулу (1) вместо поверхностного интеграла, по свойству линейности тройного интеграла, собираем все слагаемые под один интеграл и сокращаем уравнение на ∆t:
Так как здесь объем (V) является произвольным, то равенство возможно только в том случае, когда равно 0 подынтегральная функция (условия ее непрерывности считаем выполненными).
- это и есть дифференциальное уравнение состояния процесса теплопроводности, которое выполняется в любой точке (x, y, z) в момент времени t.
Чтобы привести уравнение (2) к известному виду уравнения теплопроводности, проводим его математическую обработку:
1)
2)
уравнение (2) 
f ̴ (x, y, z, t) - классическое уравнение нестационарной теплопроводности в трехмерном теле.
Здесь T = T (x, y, z, t) – температура в точке (x, y, z) в момент времени t, отсчитываемого от начала процесса теплопроводности;
a2 = k / (С∙ ρ ), где k – коэффициент теплопроводности материала, С – коэффициент теплоемкости материала, ρ – объемная плотность материала, их которого изготовлено физическое тело;
f ̴ (x, y, z, t) = f (x, y, z, t) /(С∙ ρ ), где f (x, y, z, t) – плотность распределения внутренних источников и стоков тепла, отнесенное к единице времени;
∆ = ∂2/∂x2+∂2/∂y2+∂2/∂z2 – оператор Лапласа.
Получаем уравнение состояния для решаемой физической задачи, как частный случай из рассмотренного выше общего случая.
Так как в данной (решаемой) задаче источники и стоки тепла внутри тела отсутствуют, то f (x, y, z, t) = 0, а следовательно, и f ̴ (x, y, z, t) = 0.
Вследствие того, что в решаемой задаче физическим телом является тонкий стержень с теплоизолированной боковой поверхностью, функция состояния T будет незначительно меняться в пределах любого поперечного сечения, то есть будет не зависеть от координат y, z и изменяться только по длине стержня. Следовательно T = T (x, t).
Тогда уравнение теплопроводности примет следующий вид:
Исходя из условия задачи, решаемой в данной курсовой работе, необходимо переобозначить функцию T (x, t) на функцию U (x, t).
Следовательно, окончательное дифференциальное уравнение состояния в поставленной задаче будет иметь следующий вид:
Математическая модель
1. В качестве ДУЧП берем из физики уравнение состояния, описывающее процесс распределения температуры вдоль стержня, теплоизолированного по боковой поверхности:
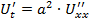(1),
где t – время, t≥0, x – координаты точки на стержне; U (x, t) – функция состояния, значения которой равны значениям температуры в каждой точке стержня; a2 – постоянная, зависящая от теплофизических характеристик материала.
Данная формула была получена при выводе уравнения состояния и будет использоваться на этапе численной реализации задачи.
2. Описываем область D, к которой относятся аргументы искомой функции U (x, t):
| l |
| t |
| x |
|
|
|
3. Граничные условия для U (x, t):
4. Начальные условия для U (x, t):
5. Краткая форма получившейся математической модели поставленной физической задачи:
|
|
| D: |
| U|t=0 = 0 |
| U|x=l = 0 |
| U|x=0 = At |
| l |
| t |
| x |
|
|
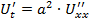
| U (x, t) -? |
| D |
6. Квалификация математической модели:
Математическая модель поставленной физической задачи получилась в виде краевой задачи Дирихле для одномерного уравнения теплопроводности, которое относится к ДУЧП параболического типа.
7. Данная краевая задача не может быть решена классическим методом Фурье, так как не выполняется условие того, что на двух противоположных сторонах прямоугольной области D должны быть заданы нулевые условия на функцию U. Следовательно, в решении нужно будет использовать модификацию метода Фурье.