Для решения ДУЧП теплопроводности: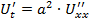 
в данной краевой задаче используем модификацию метода Фурье на случай полубесконечной прямоугольной области, на двух противоположных сторонах которой нет нулевых граничных условий для функции U (x, t).
Представим искомую функцию U (x, t) в виде суммы двух функций:
Для одной из этих функций - V (x, t) поставим аналогичную краевую задачу с нулевыми условиями на двух противоположных сторонах прямоугольной области D, которую можно решить классическим методом Фурье, вторую функцию - W (x, t) найдем подбором.
| V (x, t): |
| V|t=0 = 0 - W|t=0 |
| V|x=l = 0 |
| V|x=0 = 0 |
| l |
| t |
| x |
|
| D |
| W(x, t): |
| W|x=l = 0 |
| W|x=0 = At |
| l |
| t |
| x |
|
| D |
I. Найдем функцию W (x, t):
Находим подбором функцию W (x, t), удовлетворяющую условиям:
Этому ДУЧП можно попробовать удовлетворить, представив функцию W (x, t) в виде многочлена второй степени от аргументов x и t:
Подобрать такие коэффициенты многочлена, чтобы удовлетворить условиям (3), не удалось, так как в ходе решения получилось, что одному коэффициенту соответствовало несколько значений.
Следовательно, нужно ввести еще коэффициенты, то есть взять многочлен третьей степени по x и t:
Сначала удовлетворяем ДУЧП:
Подставляем 
в ДУЧП и требуем, чтобы оно тождественно выполнялось по всем x и t:
коэффициенты при 
Удовлетворяем остальным условиям:
коэффициенты при 
коэффициенты при 
Выбрав функцию W (x, t) в виде многочлена третьей степени с неопределенными коэффициентами получили ровно 10 различных условий на эти коэффициенты. Из этих условий определим все коэффициенты и запишем окончательный вид W (x, t).
Проверка:
ДУЧП: 
, Ɐx, Ɐt
Следовательно, функция W (x, t) подобрана верно.
II. Найдем функцию V (x, t):
Классическим методом Фурье находим функцию V (x, t), как единственное решение краевой задачи, у которой скорректированы нулевые граничные условия.
1. Искомую функцию V (x, t) ищем в виде произведения двух функций, каждая из которых зависит только от одного аргумента:
Эта функция позволяет в исходном ДУ реализовать процедуру разделения переменных:
ДУЧП: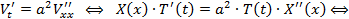 
2. Перебрасываем нулевые условия при x=0 и x=l на функцию V (x, t):
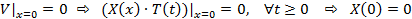
3. Решаем задачу Штурма — Лиувилля для второго уравнения системы (7) вместе с условиями (8)
т.е. найдем собственные числа 
, при которых система имеет нетривиальные решения в виде собственных функций 
.
ДУ из системы (9): 
– ДУ второго порядка относительно функции X (x) линейное, однородное с постоянными коэффициентами, поэтому
где 
– константы, 
– ФСЧР, которая находится с помощью корней характеристического уравнения.
Характеристическое уравнение имеет вид: 
1 случай: λ > 0 
– действительные различные корни k2=-k1 
Таким образом,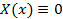 
, то есть при λ > 0 задача Штурма-Лиувилля не имеет решения.
2 случай: λ = 0 
– действительные одинаковые корни
Таким образом, 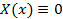, то есть при λ = 0 задача Штурма-Лиувилля не имеет решения.
3 случай: λ < 0 
– комплексные сопряженные корни
Проверка собственных значений функций на удовлетворение условиям (9):
- верно.
Таким образом, в результате решения задачи Штурма-Лиувилля получено:
4. Решаем второе уравнение системы системы (7):
Возможен только один случай – когда λ<0: при λ<0 имеем линейное однородное ДУ с постоянными коэффициентами:
– ДУ первого порядка относительно функции T(t), относится к типу ДУ с разделяющимися переменными.
5. В соответствии с формулой (6) перемножаем функции Xn(x) и Tn(t) при Ɐn=1,2,3.. и получаем счетное множество Vn (x, t):
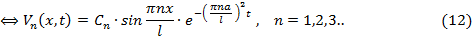
Каждая из функций (12) удовлетворяет ДУЧП и нулевым граничным условиям. По исходной задаче остается неудовлетворенным начальное условие при t=0. Для того, чтобы ему удовлетворить, функции (12) имеют произвольные константы Cn. Чтобы все эти константы использовать составим функциональный ряд из функций Vn (x, t):
Предположим, что этот ряд сходится для всех точек области D, включая ее границу, и при этом имеет равномерную сходимость в этой области, так, что его сумму можно дифференцировать через почленное дифференцирование членов ряда.
Сделав эти общие предположения относительно составленного ряда (13), обозначим его сумму через V (x, t) и получим ее получим ее выражение в следующем виде:
В силу сделанных предположений относительно ряда, имеем, что составленная функция V (x, t) удовлетворяет ДУЧП и нулевым граничным условиям, так как этому удовлетворяет каждый член ряда.
6. Удовлетворение начальному условию:
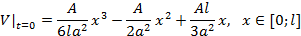
Обозначим 
– известная функция, заданная для 
- это равенство представляет собой тригонометрический ряд Фурье по синусам, составленный для функции f (x), где 
, дополненный нечетным образом на промежуток (-l; 0) и продолженный на всю числовую ось с периодом T=2l.
Следовательно, коэффициенты этого разложения вычисляются по известным формулам Фурье:
Вычисляем Сn:
Запишем функцию V (x, t), используя формулу (14) и значения коэффициентов Сn:
III. Найдем функцию U (x, t):
Складывая найденные функции V (x, t) и W (x, t), запишем функцию U (x, t):
Таким образом, используя модификацию метода Фурье, получили решение краевой задачи Дирихле для одномерного уравнения теплопроводности в полубесконечной прямоугольной области. Это решение имеет вид (16).
Управляемые параметры задачи:
A – некоторая постоянная;
l – длина стержня;
a2 – постоянная, зависящая от теплофизических характеристик материала.