Примеры решения задач
Комбинаторные задачи
При решении таких задач часто одновременно применяются и правила и формулы комбинаторики. Продемонстрируем это на примерах.
Пример 1. На книжной полке стоят 8 различных книг, из них 3 книги – по математике. Сколькими способами можно расставить эти книги так, чтобы
а) книги по математике стояли рядом;
б) книги по математике рядом не стояли?
а) Будем считать 3 книги по математике за одну, тогда получим 6 книг, которые можно расставить на полке 
способами. Учтем, что 3 книги по математике можно переставить относительно друг друга 
способами. Воспользовавшись правилом произведения, найдем n – число способов расстановки книг при указанных условиях:
.
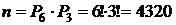б) Чтобы книги по математике рядом не стояли, можно использовать 6 мест: 4 места между книгами не по математике и по одному справа и слева от них. Число способов выбрать 3 места для книг по математике равно 
. Учитывая, что книги по математике можно переставить способами, а книги не по математике 
способами, получим, что n – общее число способов расставить книги нужным образом, равно:
.
Пример 2. Сколько имеется 5-значных чисел, в записи которых
а) ровно один раз встречается цифра 5;
б) хотя бы один раз встречается цифра 5;
в) встречается не более одной пятерки?
а) Запишем 5-значное число в виде: 
. Для записи числа можно использовать 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, которые в записи могут повторяться. Исключение составляет первая цифра, для записи которой нельзя использовать 0. Цифра 5 может стоять в числе на любом месте. Составим таблицу:
| комбинации цифр | 
| 
| 
| 
| 
|
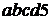
| количество чисел | 
| 
| 
| 
| 
|
Таким образом, количество 5-значных чисел, удовлетворяющих условию а) равно 
.
|
|
б) Чтобы ответить на этот вопрос, нужно из общего количества 5-значных чисел вычесть те числа, где ни разу не встречается цифра 5. Найдем общее количество 5-значных чисел: 
. Подсчитаем, в скольких 5-значных числах не встречается цифра 5: 
. Тогда общее количество 5-значных чисел, удовлетворяющих условию б), равно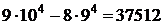 
.
в) 5-значные числа, в которых не более одной пятерки, это числа, в которых нет ни одной пятерки, и числа, в которых ровно одна пятерка. Количество тех и других установлено в пунктах а) и б). Зная их, найдем общее количество нужных нам чисел: 
.
Пример 3. Сколько можно составить автомобильных номеров, если в нем не более 4-х цифр?
Согласно условию задачи номер может содержать или одну цифру, или две, или три, или четыре цифры. Учитывая, что цифры в номере могут повторяться, а номер может начинаться с 0, найдем количество автомобильных номеров: 
.
Пример 4. В магазине продаются 6 видов пирожных. Сколькими способами можно составить набор из 4-х пирожных и из 4-х различных видов пирожных?
Поскольку при составлении набора порядок пирожных не играет роли, а сами пирожные могут повторяться, число способов составить набор это число сочетаний с повторениями по 4 из 6: 
.
При составлении набора из 4-х различных пирожных количество наборов определяется числом сочетаний без повторений по 4 из 6: 
.
Пример 5. Сколькими способами можно раздать 3 различных предмета 10 лицам, если а) каждому давать не более одного предмета; б) не ограничивать число предметов?
а) Первый предмет можно дать одному из 10, второй предмет – одному из 9, третий – одному из 8, т.е. искомое число способов равно числу размещений из 10 по 3: 
.
|
|
б) Первый предмет можно дать любому из 10 лиц, второй – тоже любому из 10, третий – любому из 10, т.е. число способов равно числу размещений с повторениями из 10 по 3: 
.
Пример 6. Сколькими способами можно раздать 3 одинаковых предмета 10 лицам?
Распределение предметов можно осуществить так: выбрать из 10 человек 3 и дать им по одному предмету; можно выбрать из 10 человек 2 и дать одному 2 предмета, другому – один (и наоборот); затем выбрать одного из 10 и дать все три предмета. Тогда искомое число способов n равно:
.
Пример 7. Сколько делителей имеет число 800?
Делителем числа 
называется натуральное число 
, на которое делится нацело. Каждое составное число можно разложить на простые множители, т.е. представить в виде: 
, где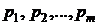 
– простые числа, 
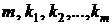– натуральные числа. Делитель имеет следующий общий вид:
,
где 
принимает 
значение: 
; а 
меняется от 1 до m. Тогда число способов составить делитель равно:
.
Разложим число 800 на простые множители: 
. Общий вид делителя 
, где a принимает 6 значений от 0 до 5, а b принимает 3 значения от 0 до 2. Следовательно, количество делителей равно: 
.
Пример 8. На автомобильной стоянке могут стоять в ряд 6 машин. Сколькими способами можно заполнить эту стоянку?
Каждое из мест может быть или занято или свободно, значит, число способов заполнить каждое место равно 2. Тогда общее число способов заполнить стоянку равно: 
.
Задачи на непосредственное вычисление вероятности события
Пример 1. В группе детского сада 30 детей. На утреннике 20 из них танцуют, 10 поют песни, а 5 и танцуют, и поют. Какова вероятность, что наугад взятый ребенок не принимает участия в празднике?
|
|
Определим, сколько детей только танцуют: 20 – 5 = 15. Теперь найдем, сколько детей только поют: 10 – 5 = 5. Учитывая тех, кто и поет, и танцует, находим, что в представлении участвуют 15 + 5 + 5 = 25 детей. Следовательно, не принимают участия в празднике 5 детей. Тогда искомую вероятность можно найти, используя формулу классической вероятности:
.
Пример 2. Имеется 15 стандартных изделий и 5 бракованных. Из них наугад выбирают два изделия. Какова вероятность, что одно из них бракованное?
Рассмотрим общую задачу. В партии из S изделий K бракованных. Найти вероятность того, что среди выбранных наугад для проверки r изделий ровно l окажутся бракованными.
Число возможных способов взять r изделий из S равно 
. Благоприятствующими являются случаи, когда из общего числа K бракованных изделий взято l, что можно сделать 
способами, а остальные r – l изделий не бракованные, т.е. они взяты из общего числа S – K, что можно сделать 
способами. Поэтому число благоприятствующих случаев равно 
. Искомая вероятность будет равна
.
Тогда для нашей задачи имеем
.
Пример 3. Два друга условились встретиться в Москве у памятника Пушкину между 12 и 13 часами. Договорились, что тот, кто пришел первым, ждет 20 минут и уходит. Какова вероятность, что друзья встретятся?
Пусть время (в часах) прихода одного 12 + x, а второго 12 + y. Это состояние изображается точкой на плоскости с координатами (x; y). Поскольку 
и 
, то эти точки (x; y) наудачу брошены в квадрат со стороной 1, и все возможные исходы изображаются точками этого квадрата, площадь которого равна 1. По условию встреча состоится, если 
, (т.к. 20 мин. = 1/3 ч.), или 
. Этому событию соответствует заштрихованная область SA, а отношение ее площади к площади квадрата равно искомой вероятности:
.
Пример 4. Найти вероятность того, что сумма двух наугад взятых правильных положительных дробей не больше 1, а произведение не больше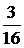 
.
Обозначим через x и y правильные положительные дроби. Рассмотрим на плоскости точку с координатами (x, y). Так как дроби выбираются произвольно, то (x, y) есть точка, наудачу брошенная на плоскость. Согласно условию задачи все возможные исходы опыта определяются системой неравенств:
Точки, удовлетворяющие этой системе, попадают в квадрат ОВАС. Благоприятствующие исходы определяются дополнительными условиями:
или 
Этой системой неравенств в квадрате ОВАС задается заштрихованная область SA, отношение площади которой к площади квадрата равно искомой вероятности. Т.к. площадь квадрата равна 1, то вероятность численно равна площади SA.
Сделаем рисунок. Уравнения границ:
– прямая, отсекающая на осях отрезки длиной 1;
– гипербола, для ее построения составим таблицу:
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| 1,8750 | 0,9375 | 0,6250 | 0,4688 | 0,3750 | 0,3125 | 0,2679 | 0,2344 | 0,2083 | 0,1875 |
Найдем абсциссы точек пересечения границ M и N. Для этого решим систему:
Тогда площадь S 1 будет равна
Окончательно имеем:
.