Задачи на дискретную случайную величину (ДСВ)

При решении таких задач важно правильно установить вид распределения ДСВ или, другими словами, правильно выбрать формулы для вычисления вероятностей отдельных значений ДСВ.

Пример 1. Передается сообщение из 5 символов, вероятность искажения отдельного символа р равна 0,1. Для случайной величины Х – числа искаженных символов в сообщении составить ряд распределения и найти числовые характеристики , и .

Передачу каждого символа можно считать отдельным испытанием, при передаче сообщения оно повторяется 5 раз. Любой символ может быть искажен или передан правильно независимо от передачи других символов. Учитывая изложенное, выбираем для Х биномиальное распределение. Случайная величина Х в нашей задаче может принимать значения 0, 1, 2, 3, 4, 5. Вероятность каждого из них можно найти по формуле Бернулли, в которой :

.

Меняя значения m от 0 до 5, составим ряд распределения:

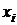
	0,59049	0,32805	0,0729	0, 0081	0,00045	0,00001

Найдем числовые характеристики:

Пример 2. Посетитель в тире купил 5 патронов и стреляет по мишени до первого попадания. Вероятность попадания р при каждом выстреле равна 0,7. Для случайной величины Х – числа сделанных выстрелов составить ряд распределения и найти числовые характеристики , и .

Т.к. выстрелы (испытания) повторяются до первого попадания (успеха), то случайная величина, описанная в задаче, имеет геометрическое распределение. Она может принимать значения 1, 2, 3, 4, 5. Вероятности первых четырех значений можно найти по формуле:

Значению соответствуют 2 события: либо стрелок попадет, либо патроны кончатся, поэтому соответствующую вероятность находим по формуле: .

Проведя вычисления, составим ряд распределения:

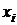
	0,7	0,21	0,063	0,0189	0,0081

Найдем числовые характеристики:

;

;

.

Пример 3. Из колоды в 36 карт наугад достают 4 карты (без возвращения). Для случайной величины Х – числа карт бубновой масти среди выбранных – составить ряд распределения и найти числовые характеристики , и .

Т.к. выборка производится без возвращения из совокупности объектов объемом , из которых объектов имеют отличительный признак, то для случайной величины выбираем гипергеометрическое распределение. Х может принимать значения 0, 1, 2, 3, 4, вероятности которых можно найти по формуле:

Вычислив вероятности, составим ряд распределения:

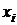
Найдем числовые характеристики:

Задача на непрерывную случайную величину (НСВ)

Плотность вероятности непрерывной случайной величины Х представлена на графике:

1) Найти вид функции .

2) Показать, что может служить плотностью вероятности случайной величины Х.

3) Найти математическое ожидание и дисперсию .

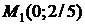1) Графиком функции вне промежутка служит ось абсцисс, а на промежутке графиком является прямая, уравнение которой нужно найти. Для этого воспользуемся уравнением прямой, проходящей через две точки и : . В нашем случае и , тогда . Следовательно, выражение для плотности вероятности имеет вид:

2) Для функции плотности вероятности должно выполняться следующее условие: . Составим интеграл от :

.

Найдем числовые характеристики: