В разделе 7 приведены формулы для нахождения числовых характеристик такой системы и коэффициента корреляции между случайными величинами, входящими в систему. В этих формулах используются вероятности 
, 
и 
. На практике в таблице, задающей систему двух ДСВ, указываются не вероятности, а частоты 
соответствующих пар значений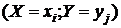 
. Если N общее количество зарегистрированных пар значений случайных величин, то нужные вероятности можно найти по формулам:
Тогда числовые характеристики можно найти с помощью средних значений:
Черта сверху обозначает среднее значение соответствующей величины. Коэффициент корреляции тогда можно найти по формуле:
.
Уравнения линий регрессии будут иметь вид:
Пример 1. Система двух ДСВ Х и Y задана таблицей:
| ||||||||||
|
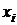
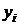
Изобразить поле рассеяния, найти коэффициент корреляции, составить уравнения линий регрессии и нарисовать их.
Найдем необходимые средние значения:
;
Найдем коэффициент корреляции:
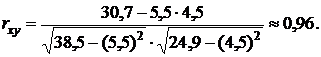
Выпишем уравнение регрессии Y по Х:
.
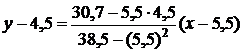После проведения вычислений это уравнение можно привести к виду:
.
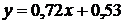Выпишем уравнение регрессии Х по Y:
.
После преобразований это уравнение можно привести к виду:
.
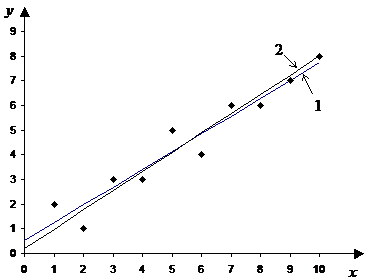
Изобразим поле рассеяния и нанесем на него линии регрессии. Полем рассеяния называется графическое изображение табличных данных в виде точек с координатами 
на плоскости 
.
На рисунке под номером 1 изображена линия регрессии Y по Х, под номером 2 – линия регрессии Х по Y. Как видно, эти линии вполне соответствуют табличным данным.
Пример 2. Система двух ДСВ Х и Y задана таблицей:
| Y | 
| |||||||
| Х | ||||||||
|
Изобразить поле рассеяния, найти коэффициент корреляции, составить уравнения линий регрессии и нарисовать их.
Найдем средние величины:
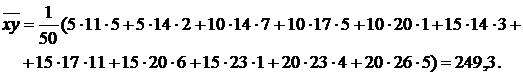
Вычислим коэффициент корреляции:
Выпишем уравнение регрессии Y по Х:
.
После проведения вычислений это уравнение можно привести к виду:
.
График данной линии нарисован на поле рассеяния под номером 1.
Выпишем уравнение регрессии Х по Y:
.
После преобразований это уравнение можно привести к виду:
.
График этой линии нарисован на поле рассеяния под номером 2.
Список литературы
1. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика: Учеб. пособие для экон. спец. вузов. – М.: Высш. шк., 1991. – 400 с.
2. Лихолетов И.И., Мацкевич И.П., Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Минск: Выш. шк., 1969. – 454 с.: ил.
3. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. – М.: Наука, 1969. – 512 с.:ил.
4. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с.:ил.
Оглавление
1. Основные понятия теории вероятностей........................................................ 3
2. Основные правила и формулы комбинаторики............................................ 8
3. Действия с вероятностями............................................................................. 12
4. Повторение независимых испытаний........................................................... 17
5. Случайные величины.................................................................................... 24
6. Виды распределений случайных величин................................................... 32
7. Системы случайных величин........................................................................ 41
8. Функции случайных величин....................................................................... 45
9. Действия со случайными величинами. Свойства математического
ожидания и дисперсии................................................................................... 47
10. Примеры решения задач ………………………………………………………51