Наряду с агрегатными индексами, как указывалось выше, общие индексы могут быть построены путем осреднения индивидуальных индексов. Преобразование агрегатного индекса в средний из индивидуальных производится путем замены либо в числителе, либо в знаменателе агрегатного индекса (там, где стоит условная величина) вместо индексируемого показателя его выражением через соответствующий индивидуальный индекс. Если замена делается в числителе, то полученный индекс называется средним арифметическим, если в знаменателе - средним гармоническим.
Так, сводный индекс объемного показателя (например, физического объема продукции (товарооборота)) из агрегатной формы может быть преобразован в средний арифметический индекс:
(
).
Сводный индекс качественного показателя (например, сводный индекс цен) из агрегатной формы может быть преобразован в средний гармонический:
(
).
Так, индекс цен позволяет определить экономию или дополнительные расходы населения на приобретение товаров от изменения цен как из сводного индекса цен в агрегатной форме или из среднего индекса:
или 
.
Рассмотрим построение средних индексов на следующем примере.
Задача 2. Имеются следующие данные по рынкам города:
| Товары | Товарооборот, тыс.грн. | Изменение в отчетном периоде по сравнению с базисным, % | ||
| базисный период | отчетный период | количества товара | цены за единицу товара | |
| А | 36,0 | 35,0 | +4,0 | +12,0 |
| Б | 64,0 | 65,0 | +41,0 | -13,7 |
| Итого | 100,0 | 100,0 | х | х |
Определить:
1. Индивидуальные и сводные индексы физического объема (количества проданных товаров), цен и товарооборота (стоимости проданных товаров).
2.Экономический эффект от изменения цен по каждому товару и в целом.
|
|
Р е ш е н и е
1. Для условных обозначений и здесь целесообразно отвести в заголовках граф отдельную (двойную) строку. Условные обозначения будут такие (табл.1).
Таблица 1
К расчету индивидуальных и сводных индексов
| Товары | 
| 
| 
| 
| 
| 
|
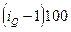
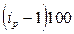
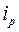
| А | ||||||
| А | 36,0 | 35,0 | +4,0 | +12,0 | 1,04 | 1,120 |
| Б | 64,0 | 65,0 | +41,0 | -13,7 | 1,41 | 0,863 |
| Итого | 100,0 | 100,0 | +27,7 | -6,2 | 1,277 | 0,938 |
На основе гр.3 и гр.4 найдем 
и 
и внесем их в таблицу в форме коэффициентов (гр.5 и гр.6).
По условию этой задачи построить сводные индексы физического объема товарооборота и цен в агрегатной форме нельзя. Вычислим индексы названных показателей (IQ и Ip) по формулам средних индексов:
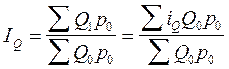, где 
,
, где 
.
Продолжение табл. 1
| Товары | 
| 
| 
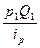
| Эр |
| А | ||||
| А | 37,44 | 31,25 | 1,1698 | 3,75 |
| Б | 90,24 | 75,31 | 1,2168 | -10,31 |
| Итого | 127,68 | 106,57 | 1,1981 | -6,57 |
.
В отчетном периоде по сравнению с базисным количество проданных товаров всех видов возросло на 27,7%.
.
В отчетном периоде по сравнению с базисным цены по всем товарным группам снизились на 6,2%.
Индексы товарооборота найдем, используя взаимосвязь индексов:
(см. гр.9 табл. 1).
2.Для расчета экономического эффекта (Э) в целом по всем товарным группам находим разность между числителем и знаменателем индекса цен, построенного в средней форме:
Аналогично может быть рассчитана экономия (дополнительные расходы) за счет изменения цены по каждому товару (гр.10 табл.1).
Так, в отчетном периоде за счет снижения цен в целом по всем товарным группам экономия населения при покупке товаров составила 6,57 тыс.грн., в том числе по товару А за счет роста цен дополнительные расходы населения на покупку товара составили 3,75тыс.грн., а по товару Б за счет снижения цен сэкономлено 10,31 тыс.грн.
|
|