Государственное образовательное бюджетное учреждение
Высшего профессионального образования
Ульяновский государственный университет
Факультет Математики и информационных технологий
Кафедра Информационных технологий
Отчет по лабораторному проекту №1
“Стандартные алгоритмы LU-разложения”
Вариант №2:
 - разложение на основе гауссова исключения по столбцам
- разложение на основе гауссова исключения по столбцам
с выбором главного элемента по активной подматрице
Выполнил: Багаутдинов Н.Р.
гр. ИТСС-О-12/1
_______________________
Проверила: доц. Цыганова Ю.В.
_______________________
Ульяновск – 2014 г.
Цель проекта: приобретение практических навыков реализации алгоритмов LU-разложения в виде программного проекта на языке MATLAB.
Задания:
1. Система меню для взаимодействия пользователя с программой и генерация исходных данных задачи.
2. Функция факторизации матрицы.
3. Функция решения системы линейных алгебраических уравнений.
4. Функция вычисления определителя матрицы.
5. Функция обращения матрицы через решение системы AX = E.
6. Функция обращения матрицы через элементарные преобразования разложения.
7. Эксперимент 1 “Решение СЛАУ для случайных матриц”.
8. Эксперимент 2 “Решение СЛАУ с плохо обусловленными матрицами”.
9. Эксперимент 3 “Обращение случайных матриц”.
Задание №1 “Система меню для взаимодействия пользователя с программой и генерация исходных данных задачи”
Взаимодействие с пользователем осуществляется через командную строку МАТЛАВ. Пользователю на выбор предлагается выбрать одно из действий: ввести данные, обработать данные (выполнить факторизацию матрицы, решить СЛАУ, вычислить определитель, вычислить обратную матрицу) или выйти из программы. Если пользователь выбирает обработку данных, но данные не введены, то программа выводит сообщение “Введите данные для обработки!” и предложит выбрать действие заново.
|
|
Программный код меню:
clc;
disp('Лабораторный проект №1 "Стандартные алгоритмы LU-разложения"');
disp('Вариант №3');
disp('Выполнил студент гр. ИТСС-О-12/1 Багаутдинов Н. Р.');
while(1)
param = input('Нажмите "1" для ввода данных;\nНажмите "2" для обработки дан-ных;\nНажмите "3" для выхода из программы\n', 's');
switch param
case '1',
A = input('Введите матрицу: \n A = \n');
n_ar =size(A);
n = n_ar(1);
b = input('Введите вектор: \n b = \n');
n_ar_b =size(A);
n_b = n_ar_b(1);
if (n_b ~= n)
disp('Размерности A и b не совпадают!');
return;
end
case '2',
if (exist('A', 'var') == 0)
disp('Введите данные для обработки!');
else
A_copy=A;
%____________________________________________________________
disp('Факторизация:');
[A, p, q, znak] = factorization(A, n);
disp('Факторизация матрицы A с учетом перестановок');
% PA - матрица с учётом перестановок
PA=printPA(A,n,p,q)
disp('Нижняя треугольная часть L');
L=tril(PA)
disp('Верхняя треугольная часть U');
U=triu(PA)-eye(n).*PA+eye(n)
B=L*U
%__________________________________________________________
% x=zeros(n,1);
% x1=zeros(n,1);
% disp('Решение СЛАУ');
% x=SLAE(A, b, n, p)
% disp('Проверка решения');
% x1=A_copy\b
% %___________________________________________________________
% disp('Детерминант матрицы A');
% d=determinant(A, n, p, znak)
% disp('Проверка детерминанта');
% d1=det(A_copy)
% %__________________________________________________________
% A11=zeros(n,n);
% A12=zeros(n,n);
% disp('Обращение матрицы через решение системы AX=E');
% A11=inversion_1(A, n, p)
% disp('Обращение матрицы через элементарные преобразования разложения');
% A12=inversion_2(A, n, p)
% disp('Проверка обращения');
% V=inv(A_copy)
|
|
end
case '3', return;
otherwise, disp('Введен некорректный символ. Введите один из предложенных.');
end
end
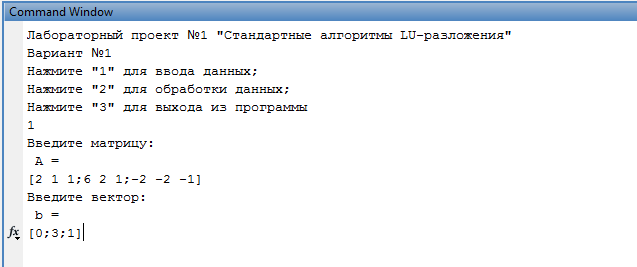
Рис 1. Пример работы меню
Задание №2 “Функция факторизации матрицы”
Алгоритм 1.  - разложение на основе гауссова исключения по активной подматрице:
- разложение на основе гауссова исключения по активной подматрице:
Для k =1 до n
Выбираем главный элемент в A ( k -1).
Нормируем первую строку матрицы A ( k -1).
Для i = k +1 до n
Вычитаем первую строку матрицы A ( k -1), умноженную на aik ( k -1),
из i -й строки.
Стратегия выбора главного элемента по активной подматрице заключается в том, что на каждом шаге k работы алгоритма факторизации выбирается макси- мальный по модулю элемент среди элементов, лежащих в столбцах от k-го до n-го и в строках от k-ой до n-ой (для прямых алгоритмов) или лежащих в столбцах от 1-го до k-го и в строках от 1-ой до k-ой (для обратных алгоритмов).
Здесь в качестве
главного выбирается максимальный по модулю элемент активной подмат-
рицы. В общем случае, чтобы поставить этот элемент на место диагональ-
ного, требуется обменивать столбцы и строки матрицы A(k−1), что связано с
введением двух дополнительных векторов: в одном хранятся перестановки
столбцов, а в другом перестановки строк матрицы A.
.
Программный код функции факторизации (  - разложение ):
- разложение ):
function [A, p, q, znak, op_numb] = factorization(A, n)
p = zeros(n,1);
q = zeros(n,1);
%вспомогательные переменные
max = 0;
imax = 0;
jmax = 0;
buf = 0;
znak=1;
op_numb=0;
% заполняем массивы перестановок начальными значениями перед нача-лом факторизации
for i=1:n
p(i)=i;
q(i)=i;
end
% этот фрагмент вставляем в алгоритм факторизации
% n – номер задачи, k – номер текущего шага алгоритма
|
|
for k=1:n
%_____________________________________________________
max=abs(A(p(k),q(k)));
imax=k;
jmax=k;
for i=k:n
for j=k:n
if(abs(A(p(i),q(j)))>max)
max=abs(A(p(i),q(j)));
imax=i;
jmax=j;
end
end
end
% обмен
if(imax ~= k)
znak=-znak;
buf=p(k);
p(k)=p(imax);
p(imax)=buf;
end
if(jmax ~= k)
znak=-znak;
buf=q(k);
q(k)=q(jmax);
q(jmax)=buf;
end
%____________________________________________________
div = A(p(k),q (k));
for j=(k+1):n
A(p(k),q(j))= A(p(k),q(j))/div;%Нормировка
op_numb = op_numb + 1;
end
for i=(k+1):n
mult = A(p(i),q (k));
for j=(k+1):n
A(p(i),q (j))= A(p(i),q (j))- mult *A(p(k),q (j));
op_numb = op_numb + 1;
end
end
end

Рис 2. Вывод результатов факторизации
Задание №3 “Функция решения системы линейных алгебраических уравнений”
Поиск решения СЛАУ осуществляется по 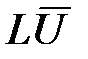 разложению. Решение находим в два этапа: сначала находится решение для системы с нижней треугольной матрицей, затем находится решение с верхней треугольной матрицей. Математическое обоснование:
разложению. Решение находим в два этапа: сначала находится решение для системы с нижней треугольной матрицей, затем находится решение с верхней треугольной матрицей. Математическое обоснование: 
Программный код функции решения СЛАУ:
function [x, op_numb] = SLAE(A, b, n, p, q)
y = zeros(n,1);
x = zeros(n,1);
op_numb = 0;
for i=1:n
sum=0;
for j=1:i
sum =sum+A(p(i),q(j))*y(j);
op_numb = op_numb + 1;
end
y(i)=(b(p(i))-sum)/A(p(i),q(i));
op_numb = op_numb + 1;
end
for i=n:-1:1
sum=0;
for j=i+1:n
sum =sum+A(p(i),q(j))*x(q(j));
op_numb = op_numb + 1;
end
x(q(i))=y(i)-sum;
end
end

Рис 3. Вывод результатов решения СЛАУ
Задание №4 “Функция вычисления определителя матрицы”
Определитель находится как произведение диагональных элементов в разложенной матрице, поскольку 
(определитель треугольной матрицы с единичной диагональю равен 1, а определитель треугольной матрицы равен произведению диагональных элементов).
Так как используется первая стратегия выбора главного элемента, то при работе алгоритма факторизации происходит обмен строк и столбцов. При этом каждый раз при обмене знак определителя меняется на противоположный. Для учёта знака в программе используется переменная-флаг znak, в котором сохраняется значение -1 или 1, в зависимости от того, чётное или нечётное количество перестановок было сделано на данный момент.
Программный код функции вычисления определителя:
function [det] = determinant(A, n, p,q, znak)
det=1;
for i=1:n
det=det*A(p(i),q(i));
end
det= det*znak;
end

Рис 4. Вывод результатов вычисления определителя
Задание №5 “Функция обращения матрицы через решение системы AX=E”
Решение осуществляется исходя из равенства AX=E, где X – обратная матрица, E – единичная матрица. Разобьём матрицы X и E на столбцы и запишем систему СЛАУ:
 , где xk – k -ый столбец матрицы X, ek – k -ый столбец матрицы E.
, где xk – k -ый столбец матрицы X, ek – k -ый столбец матрицы E.
Учитывая, что известно 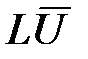 - разложение матрицы A, каждая из СЛАУ решается алгоритмом, описанном в задании № 3. Столбцы обратной матрицы находятся по очереди и затем собираются вместе.
- разложение матрицы A, каждая из СЛАУ решается алгоритмом, описанном в задании № 3. Столбцы обратной матрицы находятся по очереди и затем собираются вместе.
Программный код функции обращения матрицы через решение системы AX=E:
function [V, count_ops_1] = inversion_1(A, n, p, q)
V = zeros(n,n);
I = eye(n);
count_ops_1 = 0;
count_ops_cur = 0;
for count = 1:n
b = I(:,count);
y = zeros(n,1);
x = zeros(n,1);
[x,count_ops_cur]=SLAE(A, b, n, p, q);
V(:,count) = x;
count_ops_1 = count_ops_1 +count_ops_cur;
end
end
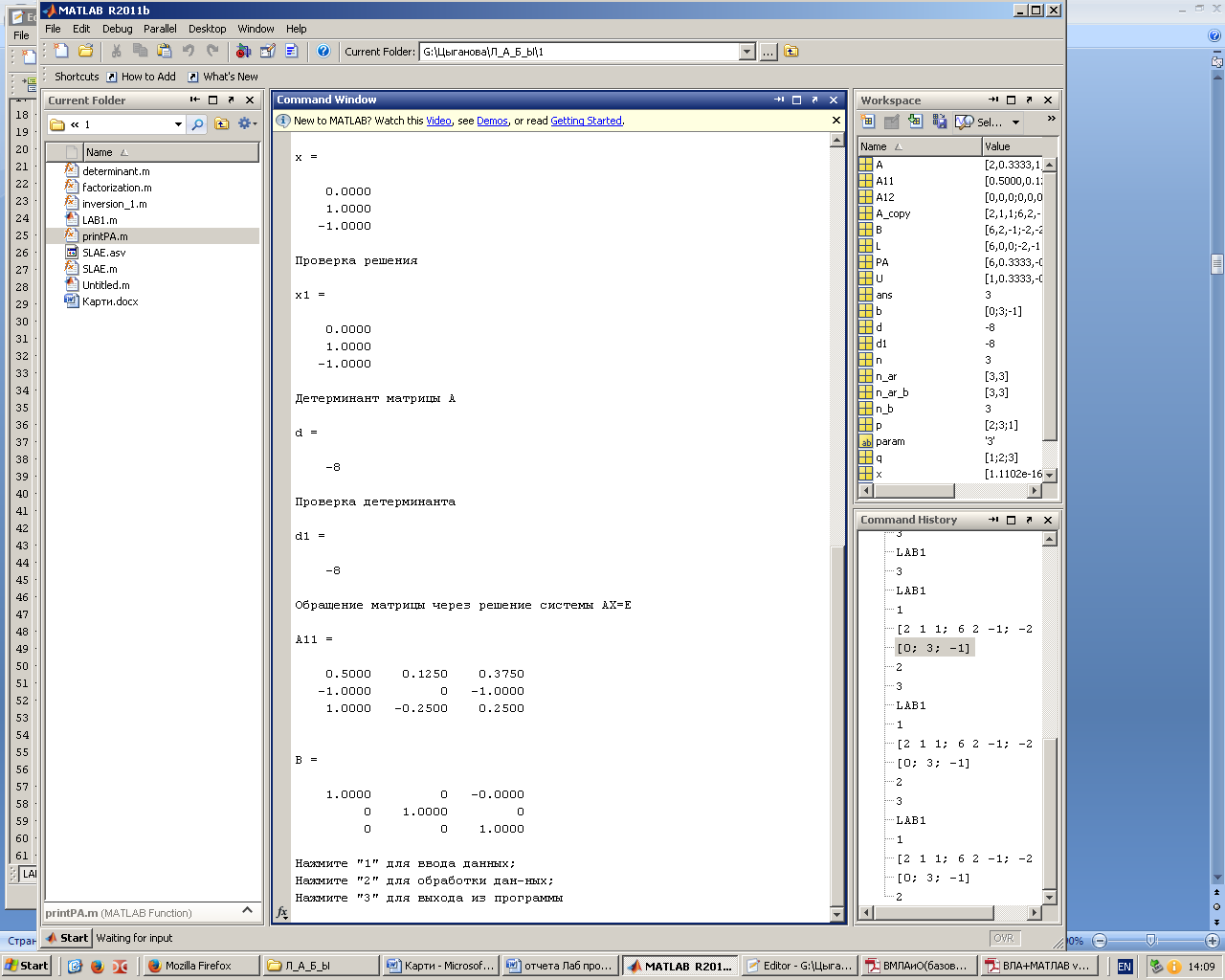
Рис 5. Вывод результатов обращения матрицы через решение системы AX=E
Задание № 6 “Функция обращения матрицы через элементарные
преобразования”
Пусть 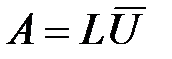 . Тогда
. Тогда  . Матрицы L и
. Матрицы L и  уже известны. Следовательно, сначала найдём обратные к ним, а затем найдём их произведение и получим матрицу, обратную к A.
уже известны. Следовательно, сначала найдём обратные к ним, а затем найдём их произведение и получим матрицу, обратную к A.
Программный код функции обращения матрицы через элементарные преобразования разложения:
function [A_ob, count_ops_2] = inversion_2(A, n, p,q)
count_ops_2 = 0;
% Первый этап - подготовка (обращение элементарных матриц)
for i=1:n
for j=(i+1):n
A(p(i),q(j))=-A(p(i),q(j));
end
end
for j=1:n
A(p(j),q(j))=1/A(p(j),q(j));
count_ops_2=count_ops_2+1;
for i=(j+1):n
A(p(i),q(j))=-A(p(i),q(j))*A(p(j),q(j));
count_ops_2=count_ops_2+1;
end
end
disp('Результат выполнения первого этапа');
PA=printPA(A,n,p,q)
% Считаем матрицу U^{-1}
for k=n:(-1):2
for i=1:(k-2)
for j=k:n
A(p(i),q(j))= A(p(i),q(j))+A(p(i),k-1)*A(p(k-1),q(j));
count_ops_2=count_ops_2+1;
end
end
end
% Считаем матрицу L^{-1}
for k=1:(n-1)
for i=(k+2):n
for j=1:k
A(p(i),q(j))=A(p(i),q(j)) + A(p(i),k+1)*A(p(k+1),q(j));
count_ops_2=count_ops_2+1;
end
end
for j=1:k
A(p(k+1),q(j))=A(p(k+1),q(j)) * A(p(k+1),q(k+1));
count_ops_2=count_ops_2+1;
end
end
disp('Результат выполнения второго этапа');
PA=printPA(A,n,p,q)
% Перемножаем в одной матрице U^{-1} на L^{-1}
for i=1:n
for j=1:n
if(i<j)
sum=0;
for k=j:n
sum = sum +A(p(i),k)*A(p(k),q(j));
count_ops_2=count_ops_2+1;
end
end
if(i>=j)
sum =A(p(i),q(j));
for k=i+1:n
sum = sum +A(p(i),k)*A(p(k),q(j));
count_ops_2=count_ops_2+1;
end
end
A(p(i),q(j))=sum;
end
end
disp('Результат выполнения третьего этапа');
% Учитываем перестановки срок
A_ob=printPA1(A,n,p,q);
end
Вспомогательная функция для учёта обратной перестановки столбцов:
% Вспомогательная функция для учёта обратной перестановки столбцов:
function [ PA1 ] = printPA1(A,n,p,q)
% Учитываем перестановки строк при обращении
% Вектор обратных перестановок строк
p1=zeros(n,1);
for i=1:n
p1(p(i))=i;
end
for i=1:n
for j=1:n
PA1(i,j)=A(p(i),p1(j));
end
end
end

Рис 6. Вывод результатов обращения матрицы через элементарные преобразования разложения
Задание № 7 “Эксперимент 1 “Решение СЛАУ”
Цель данного эксперимента – исследовать скорость и точность решения СЛАУ. В ходе эксперимента определяется число операций умножения и деления, точность и скорость решения СЛАУ со случайно сгенерированными матрицами порядка от 5 до 100 (через 5 порядков). Значения элементов матриц генерируются в диапазоне от -100 до 100. Результаты эксперимента записываются в файл, а затем выводятся на экран в виде таблицы и графиков.
Программный код эксперимента №1:
function [] = exp1()
clc();
frmt = get(0,'Format');
frmtV = get(0,'FormatSpacing');
format('shortG')
format('compact')
exp_Data = zeros(1,100);
count = 1;
for n=5:5:100
exp_Data(count) = n;
count = count+1;
A = randi([-100,100],n,n);
A_copy=A;
b = randi([-100,100],n,1);
% Засекаем время
tic
[A, p,q, znak, op_numb] = factorization(A, n);
[x, op_numb_2] = SLAE(A, b, n, p, q);
exp_Data(count) = toc;
count = count+1;
x_ex = zeros(n,1);
b_ex = zeros(n,1);
for i=1:n
x_ex(i) = i;
end;
% Вычисляем правую вектор b для точного решения
for i=1:n
for j=1:n
b_ex(i) = b_ex(i) + A_copy(i,j) * x_ex(j);
end
end
[x_calc] = SLAE(A, b_ex, n, p, q);
% Вычисляем точность найденного решения
for i=1:n
ex = abs(x_ex(i) - x_calc(i));
if (i == 1)
max_ex = ex;
else
if (ex > max_ex)
max_ex = ex;
end
end
end
exp_Data(count) = max_ex;
count = count +1;
exp_Data(count) = n^3/3;
count = count +1;
exp_Data(count) = op_numb + op_numb_2;
count = count + 1;
end
dlmwrite('file.dat',exp_Data,';');
clear A;
clear exp_Data;
n_ar = zeros(1,20);
time_ar = zeros(1,20);
ex_ar = zeros(1,20);
th_numb_ar = zeros(1,20);
fact_numb_ar = zeros(1,20);
read_data = dlmread('file.dat', ';');
count = 1;
% Вывод таблицы
disp(' Порядок Время Точность Теоретическое ЧО Реальное ЧО');
for i=1:5:100
n_ar(count) = read_data(i);
time_ar(count) = read_data(i+1);
ex_ar(count) = read_data(i+2);
th_numb_ar(count) = read_data(i+3);
fact_numb_ar(count) = read_data(i+4);
count = count + 1;
str = [round(read_data(i)), read_data(i+1), read_data(i+2), round(read_data(i+3)), round(read_data(i+4))];
disp(str);
end
% Вывод графиков
plot(n_ar, time_ar, 'k');
title('Зависимость времени решения от размера матрицы A (мск)');
grid on;
figure;
plot(n_ar, ex_ar, 'k');
title('Зависимость точности решения от размера матрицы A');
grid on;
figure;
plot(n_ar, th_numb_ar, n_ar, fact_numb_ar,'--');
title('Реальное и теоретическое количество операций');
grid on;
legend('Теоретич. ЧО','Реальное ЧО',2);
format(frmt)
format(frmtV)
end
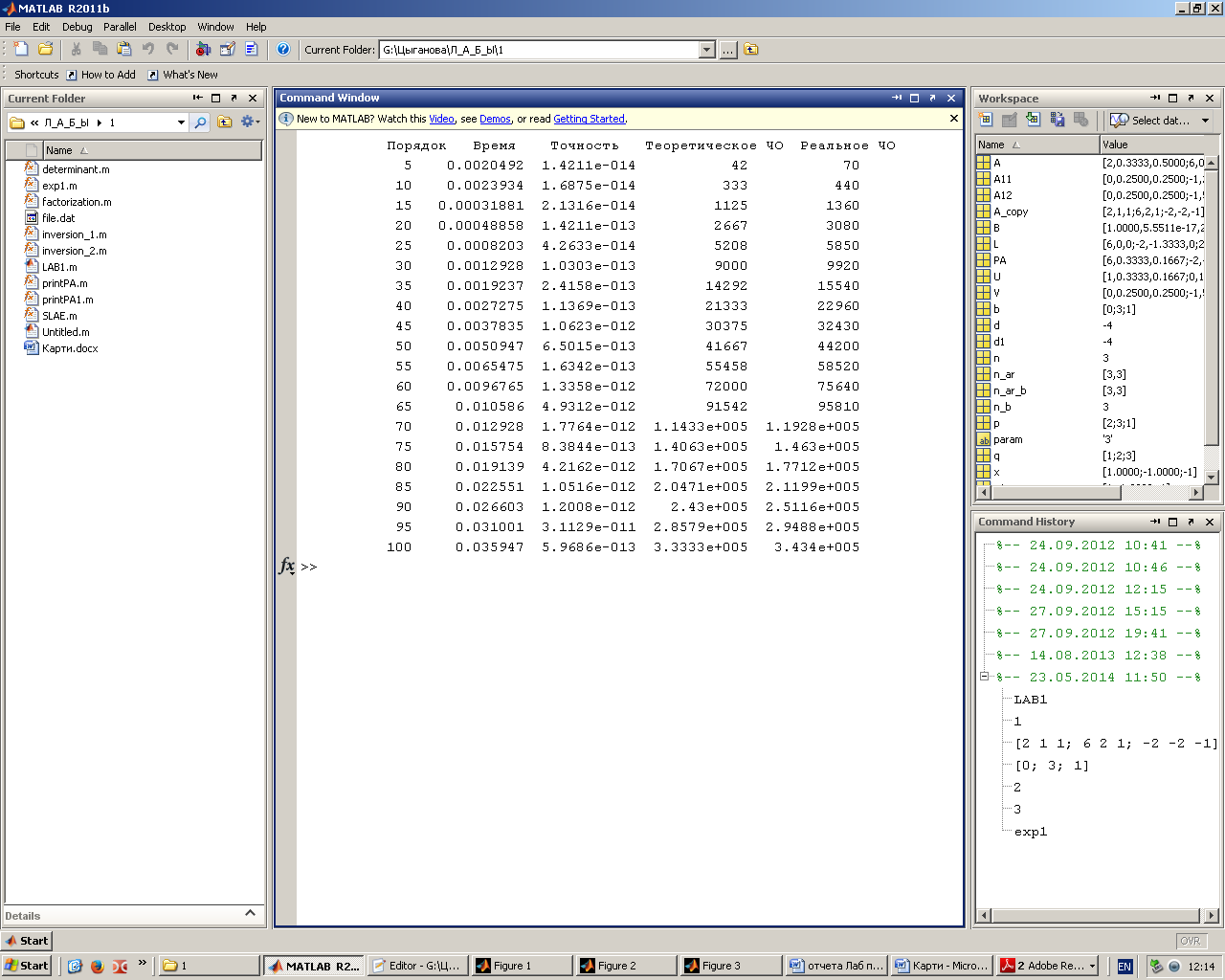
Рис 7. Таблица экспериментальных данных для решения СЛАУ

Рис 8. График зависимости времени решения от порядка матриц для решения СЛАУ

Рис 9. График зависимости точности решения от порядка матриц для решения СЛАУ

Рис 10. График зависимости реального и теоретического числа операций от размера матрицы для решения СЛАУ
Задание №8 “Эксперимент 2
“Решение СЛАУ с плохо обусловленными матрицами”
Цель данного эксперимента – исследовать скорость и точность решения СЛАУ с плохо обусловленными матрицами.
В ходе эксперимента определяется число операций умножения и деления, точность и скорость решения СЛАУ для различных видов плохо обусловленных матриц. Результаты записываются в файл, а затем выводятся на экран в виде таблицы и графиков. Программный код аналогичен программному коду для эксперимента 1, кроме генерации матриц: плохо обусловленные матрицы нефиксированного размера генерируются порядка от 4 до 40 (через 4). Графики зависимости времени решения, точности от размера матриц приведены только для матриц нефиксированного размера. Графики зависимости числа операций не строим, так как они являются аналогичными графикам эксперимента 1.