Сечение сферы плоскостью

Сфера всякой плоскостью пересекается по окружности. Если секущая плоскость параллельна плоскости проекций, то окружность проецируется на эту плоскость в натуральную величину.

Окружность, лежащая в наклонной плоскости, проецируется в эллипс.

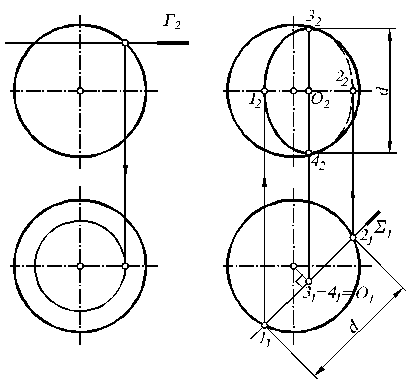
В сечении сферы плоскостью Σ получается окружность диаметром d, равным отрезку 1₁-2₁. У этой окружности – множество диаметров и все они как-то искажены при проецировании на плоскости П₂ и П₃. Самое большое искажение у диаметра 1-2: отрезок 1₂-2₂ соответствует малой оси эллипса. И только один из всех диаметров – диаметр 3-4, перпендикулярный плоскости П₁, а следовательно, параллельный плоскостям П₂ и П_3, проецируется на эти плоскостив натуральную величину и определяет большую ось эллипса (отрезок 3₂-4₂).

Пример. Построить проекции линии пересечения сферы плоскостью Λ.

Решение. В сечении сферы фронтально-проецирующей плоскостьюполучается окружность диаметром 1₂-2₂, которая на плоскости П₁ и П₃ проецируется в эллипсы.

1.Характерные точки

1.1 Точки 1₂, 2₂ – на фронтальном очерке сферы; проекции этого отрезка на

плоскости П₁ и П₃ – малые оси эллипсов: 1₁-2₁ и 1₃-2₃ соответственно.

1.2 Точка 3₂=4₂ – проекция большой оси эллипса. Она лежит в середине отрезка 1₂-2₂ и совпадает с проекцией центра окружности, которая получилась в сечении. Можно найти эту точку, опустив перпендикуляр из центра сферы на плоскость Λ. Горизонтальная и профильная проекции отрезка 3-4 (3₁-4₁ и 3₃-4₃) лежат на соответствующих линиях связи и равны диаметру окружности (длине отрезка 1₂-2₂). 1.3 Точки 5 и 6 лежат на профильном очерке сферы; очевидные.

1.4 Точки 7 и 8 – на горизонтальном очерке сферы; очевидные.

2. Промежуточные точки 9 и 10 определены с помощью параллели m.

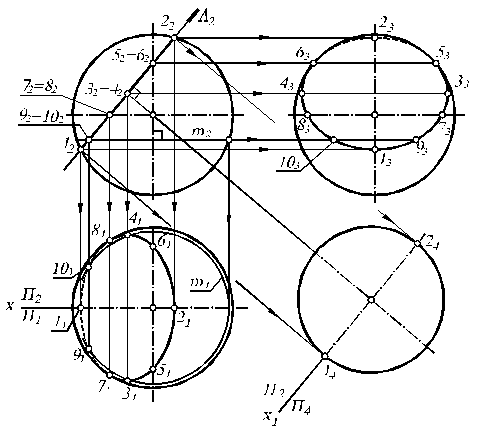
3. Определение видимости кривой. На горизонтальной проекции границы видимости – точки 7 и 8 – на горизонтальном очерке. Участок эллипса 7-1-8 –невидимый, так как лежит на нижней половине сферы.

На профильной проекции границы видимости – точки 5 и 6 – на профильном очерке. Участок эллипса 6-2-5 –невидимый, так как лежит на невидимой половине сферы.

4. Натуральный вид фигуры сечения – окружность (но не эллипс!).

Линейчатой называют поверхность, которая образуется движением прямой линии (образующей) в пространстве. В зависимости от закона движения образующей прямой 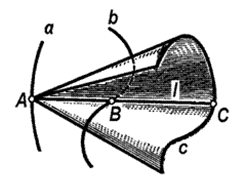выделяют три вида линейчатых поверхностей. Линейчатые поверхности с тремя направляющими образуются движением прямолинейной образующей по трем направляющим a, b и c (кривым или прямым), которые единственным образом определяют движение образующей l. Так, выбрав на направляющей a любую точку А, можно будет провести через эту точку бесконечное множество прямолинейных образующих конической поверхности

Рисунок 1

с вершиной в точке А и пересекающих направляющую c. Из рисунка1 видно, что через точку А, взятую на направляющей a,проходит одна и только одна прямолинейная образующая, пересекающая две другие направляющие b и c.

Описанным способом через точки, принадлежащие направляющей a,можно построить любое число прямолинейных образующих, которые выделят в пространстве одну единственную линейчатую поверхность.

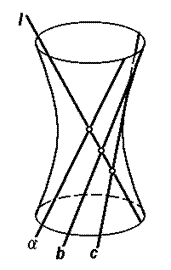
Рисунок 2

Примером линейчатой поверхности с тремя направляющими является однополосный гиперболоид, у которого направляющими служат три произвольно скрещивающиеся прямые a, b и c (рис. 2).

Часто линейчатые поверхности задаются меньшим числом направляющих. В этих случаях отсутствие недостающих направляющих дополняют условиями, обеспечивающими заданный характер движения образующей. Для получения линейчатых поверхностей с двумя направляющими задается дополнительное условие сохранения параллельности образующей какой-либо плоскости, называемой плоскостью параллелизма, или сохранения заданного угла наклона образующей относительно какой-либо плоскости или оси вращения (у геликоидов). Такие поверхности называются поверхностями с плоскостью параллелизма. К ним относятся:

- цилиндроид образуется движением прямолинейной образующей l по двум криволинейным направляющим a и b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма Σ

Рисунок 3.

- коноид образуется движением прямолинейной образующей l по двум направляющим, из которых одна является кривой линией a, а другая – прямой b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма Σ.

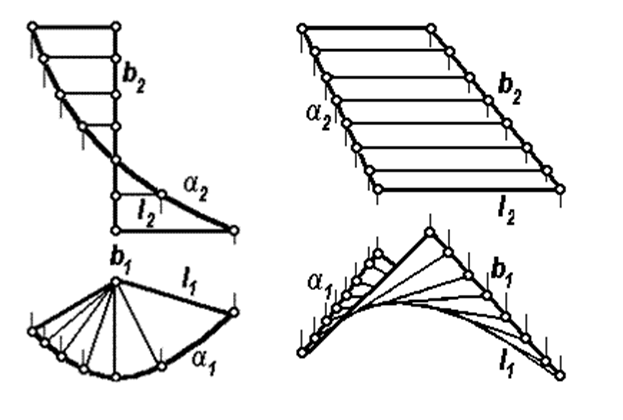
Рисунок 4. Рисунок 5.

На рис. 4 изображена косая плоскость, направляющими которой служат

прямые a и b, а плоскость параллелизма – горизонтальная плоскость проекций П1, следовательно, образующие косой плоскости являются горизонталями.

Так как в сечении косой плоскости можно получить, кроме прямолинейных образующих и направляющих, также гиперболу и параболу, эту поверхность еще называют гиперболическим параболоидом. Параболой является горизонтальный очерк косой плоскости, приведенной на рис. 5.

- торс образуется движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой m, называемой ребром возврата. Ребро возврата является направляющей торса, который полностью определяет поверхность