Если жидкость из какого-либо резервуара входит в прямую трубу постоянного диаметра и движется по ней ламинарным потоком, то распределение скоростей вначале получается практически равномерным, особенно если вход выполнен с закруглением (рис. 4.8). Но затем под действием сил вязкости происходит следующее перераспределение скоростей по сечениям: слои жидкости, прилежащие к стенке, тормозятся, а центральная часть потока (ядро), где еще сохраняется равномерное распределение скоростей, движется ускоренно, что обусловлено необходимостью пропустить определенный расход через неизменную площадь. При этом толщина слоев заторможенной жидкости постепенно увеличивается, пока не сделается равной радиусу трубы, т.е. пока слои, прилежащие к противоположным стенкам, не сомкнутся на оси трубы. Только тогда устанавливается характерный для ламинарного течения параболический профиль скоростей.
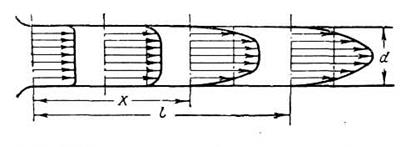
Рис. 4.8. Формирование параболического профиля скоростей в потоке жидкости
| То расстояние от начала трубы, на котором происходит установление (стабилизация) параболического профиля скоростей, называется начальным участком течения (lнач). |
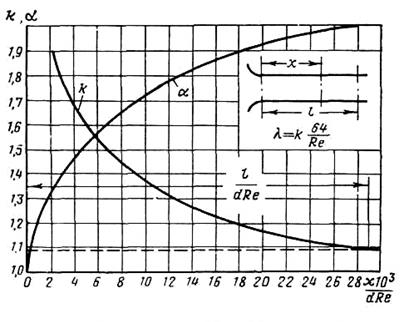
Рис. 4.9. Распределение коэффициентов К и a
Для определения длины начального участка можно пользоваться следующей приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Рейнольдса:
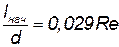
| (4.19) |
Подставив в формулу (4.19) Reкр=2300, получим максимально возможную длину начального участка, равную 66,5 диаметра.
Как указывалось выше, сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объясняется это тем, что значение производной dv/dy у стенки трубы на начальном участке больше, чем на участках стабилизированного течения, а потому больше и касательное напряжение, определяемое законом Ньютона, и притом тем больше, чем ближе рассматриваемое сечение к началу трубы, т.е. чем меньше координата х.
Потеря напора на участке трубы, длина которого l<lнач, определяется по формулам (4.15 - 4,17), но с поправочным коэффициентом К, большим единицы. Значения этого коэффициента могут быть найдены по графику (рис. 4.9), где коэффициент К изображен как функция безразмерного параметра (х/Re d) 103. С увеличением этого параметра коэффициент К уменьшается и при
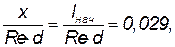
т.е. при х=lнач, делается равным 1,09. Следовательно, сопротивление всего начального участка трубы на 9% больше, чем сопротивление такого же участка трубы, взятого в области стабилизированного ламинарного течения.
Для коротких труб значения поправочного коэффициента К, как видно из графика, весьма существенно отличаются от единицы.
В том случае, когда длина трубы l больше длины начального участка lнач, потеря напора будет складываться из потери на начальном участке и потери на участке стабилизированного течения, т.е.

Учитывая формулы (4.15 - 4,17), и выполняя преобразования и подсчет, окончательно получим
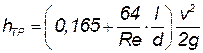
| (4.20) |
Если относительная длина трубопровода l/d достаточно велика, то дополнительный член в скобках, равный 0,165, можно за малостью отбросить. Но при уточненных расчетах труб, длина которых соизмерима с lнач, этот член следует учитывать.
Для начального участка трубы с плавным входом коэффициент a возрастает от 1 до 2 (см. рис. 4.9).