Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений в процессе течения. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсацию, например, скорости по времени, то получим картину, подобную показанной на рис. 4.14. Величина скорости беспорядочно колеблется около некоторого осредненного по времени значения vоср, которое в данном случае остается постоянным.

Рис. 4.14. Пульсации скорости в потоке

Рис. 4.15. Линии тока в турбулентном потоке
Траектории частиц, проходящих через данную неподвижную точку пространства, в разные моменты времени представляют собой кривые линии различной конфигурации несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рис. 4.15). Таким образом, строго говоря, турбулентное течение является неустановившимся течением, так как величины скоростей и давлений, а также траектории частиц меняются по времени. Однако в расчетах его можно рассматривать как установившееся при условии, что осредненные по времени значения скоростей и давлений, а также величина полного расхода потока, не меняются с течением времени. Такое течение жидкости встречается на практике достаточно часто.
Ввиду того, что при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае неприменим. Вследствие перемешивания жидкости и непрерывного переноса количеств движения в поперечном направлении касательное напряжение на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном при тех же значениях числа Re и динамического давления, подсчитанных по средней скорости потока.

Рис. 4.16. Профили скоростей в турбулентном и ламинарном потоке

Рис. 4.17. Зависимость a от Re
Распределение скоростей (осредненных по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения.
Если сравнить кривые распределения скоростей в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), но при ламинарном и турбулентном режимах, то будет заметно существенное различие в указанных кривых (рис. 4.16). Распределение скоростей при турбулентном режиме более равномерно, а нарастание скорости у стенки - более крутое, чем при ламинарном режиме, для которого, как уже известно, характерен параболический закон скоростей.
В связи с этим коэффициент a, учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном режиме значительно меньше, нежели при ламинарном. В отличие от ламинарного режима, где а не зависит от числа Re, здесь коэффициент а является функцией числа Re, уменьшаясь с увеличением последнего от 1,13 при Re=Reкр, до 1,025 npи Re=3 106. Как видно из графика, приведенного на рис. 4.17, кривая a по Re асимптотически приближается к единице. В большинстве случаев при турбулентном течении можно принимать a=1.
Потери энергии при турбулентном течении жидкости в трубах постоянного сечения (т.е. потери напора на трение) также получаются иными, нежели при ламинарном. В турбулентном потоке потери напора на трение значительно больше, чем в ламинарном при тех же размерах, расходе и вязкости.
Это увеличение потерь вызывается вихреобразованиями, перемешиванием и искривлением траекторий. Если при ламинарном режиме течения потеря напора на трение возрастает пропорционально скорости (а также расходу) в первой степени, то при переходе к турбулентному режиму заметен некоторый скачок сопротивления и затем более крутое нарастание величины hТР по кривой, близкой к параболе второй степени.
Ввиду сложности турбулентного режима течения и трудностей его аналитического исследования, до сих пор мы еще не имеем достаточно строгой и точной теории этого течения. Существуют так называемые полуэмпирические, приближенные теории турбулентности Прандтля, Кармана и др., одна из которых будет рассмотрена в следующем параграфе.

Рис. 4.18. Зависимость hТР от скорости и Q
В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются чисто экспериментальными данными, систематизированными на основе гидродинамической теории подобия.
Основной расчетной формулой для турбулентного течения в круглых трубах является уже приводившаяся выше универсальная формула (4.20), которая непосредственно вытекает из соображений подобия и имеет следующий вид:

или

| (4.30) |
где lТ - коэффициент потерь на трение при турбулентном режиме.
Эта основная формула применима как при турбулентном, так и при ламинарном режимах различие заключается в значениях коэффициента l.
Так как при турбулентном течении потеря напора на трение приблизительно пропорциональна квадрату скорости (и квадрату расхода), то коэффициент потерь на трение в формуле (4.30) в первом приближении для данной трубы можно считать величиной постоянной.
Однако из закона гидродинамического подобия следует, что коэффициент lТ, так же как и lЛ, должен являться функцией основного критерия подобия, т.е. числа Рейнольдса, включающего в себя скорость, диаметр и вязкость, т.е.

Существует ряд эмпирических и полуэмпирических формул, выражающих эту функцию для турбулентного течения в гладких трубах; одной из наиболее удобных и употребительных является формула П.К. Конакова, имеющая следующий вид

| (4.31) |
и применима от Re=Reкр до Re, равного нескольким миллионам.
При числах Рейнольдса 2300<Re<105 можно пользоваться также старой формулой Блазиуса

| (4.32) |

Рис. 4.19. Зависимость l от Re
Отсюда видно, что с увеличением числа Re коэффициент lТ уменьшается, однако это уменьшение гораздо менее значительно, чем при ламинарном режиме (рис. 4.19).
Это различие в законах изменения коэффициента l связано с тем, что непосредственное влияние вязкости жидкости на сопротивление в турбулентном потоке гораздо меньше, чем в ламинарном. Если в последнем потери напора на трение прямо пропорциональны вязкости, то в турбулентном потоке эти потери пропорциональны вязкости в степени 1/4. Дело в том, что основную роль в турбулентном потоке играют перемешивание и перенос количества движения.
Приведенные формулы (4.31) и (4.32) для определения коэффициента потерь на трение lТ через число Re справедливы для так называемых технически гладких труб, т.е. для таких, шероховатость которых столь мала, что на сопротивление практически не влияет. К числу технически гладких труб можно без большой погрешности отнести цельнотянутые трубы из цветных металлов (включая и алюминиевые сплавы), а также бесшовные стальные трубы тщательного изготовления. Таким образом, трубы, употребляемые на самолетах в качестве топливопроводов и для гидропередач (гидросистем), в обычных условиях можно считать гладкими и для их расчета пользоваться приведенными формулами. Водопроводные стальные и чугунные трубы уже нельзя считать гладкими, так как они обычно дают повышенное сопротивление, и формулы (4.31) и (4.32) для них не справедливы. Как следует из теории подобия и как показывают опыты ряда исследователей (И.И. Никурадзе, Г.Г. Гуржиенко, Рейхардта и др.), при турбулентном течении жидкости в трубах непосредственно на стенке трубы обычно имеется так называемый ламинарный слой (рис. 4.20). Это весьма тонкий слой жидкости, движение в котором является наиболее замедленным, слоистым и без перемешивания, т.е. ламинарным.
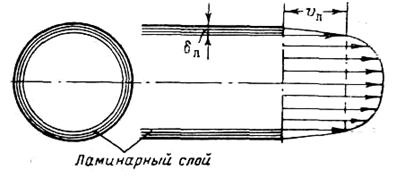
Рис. 4.20. Пограничный ламинарный слой в турбулентном потоке
В пределах этого ламинарного слоя скорость круто нарастает от нулевого значения на стенке до некоторой конечной величины vл на границе слоя. Толщина ламинарного слоя dл крайне невелика, причем оказывается, что число Re, подсчитанное по размеру dл, скорости vл и кинематическому коэффициенту вязкости n, есть величина постоянная, т.е.
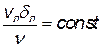
| (4.33) |
Эта величина имеет универсальное постоянное значение подобно тому, как постоянно критическое число Re для течения в трубах. Поэтому при увеличении скорости потока и, следовательно, числа Re, растет также скорость vл, а толщина ламинарного слоя dл уменьшается. При больших числах Re ламинарный слой практически исчезает.