Опыт показывает, что при ламинарном течении в малых зазорах и капиллярах, происходящем под действием больших перепадов давления порядка нескольких сотен атмосфер, падение напора вдоль потока оказывается существенно нелинейным, а закон Пуазейля дает заметную погрешность.
Объясняется это тем, что расход жидкости Q при ламинарном течении пропорционален перепаду давления Dр, а величина потерянной энергии, равная произведению QDр, пропорциональна квадрату перепада давления. Поэтому потеря энергии на единицу расхода жидкости растет пропорционально перепаду давления. Это влечет за собой нагревание жидкости при больших перепадах давления и уменьшение ее вязкости, причем степень влияния этого фактора будет нарастать вдоль потока жидкости.
С другой стороны, ввиду того, что вязкость жидкости возрастает с увеличением давления, величина вязкости в начале потока будет повышенной, но она будет уменьшаться вдоль потока вследствие падения давления. Таким образом, вязкость жидкости получается переменной вдоль потока и, как результат одновременного действия двух указанных факторов, продольный градиент давления dp/dx, обусловленный трением, оказывается в начале потока больше, а в конце потока меньше, чем это следует из закона Пуазейля.
Что касается расхода, то повышение температуры способствует его увеличению, а высокое давление в жидкости - его уменьшению по сравнению со значением, вытекающим из закона Пуазейля, т.е. влияние этих двух факторов на расход является противоположным. Однако полной компенсации обычно не получается, особенно в тех случаях, когда имеет место значительный отвод тепла через стенки и, следовательно, малое повышение температуры.
Особенно часто с описанным видом ламинарного течения приходится сталкиваться в высоконапорных гидравлических машинах, где происходит перетекание вязкой жидкости через малые зазоры под действием больших перепадов давления.
Рассмотрим задачу о ламинарном течении в зазоре величиной а, длиной l и шириной b с учетом переменности вязкости от изменения давления и температуры. При этом будем считать, что плотность жидкости от давления и температуры не зависит, а соотношение размеров зазора а/b→0.
Для одновременного учета влияния давления и температуры на вязкость жидкости можно использовать следующую зависимость

| (4.21) |
Здесь индекс"1"относит величины к началу потока.
Поместив начало координат в начальном сечении потока (рис. 54), выделим элементарный объем жидкости в форме прямоугольного параллелепипеда, симметричного относительно оси х и имеющего размеры 2y´1х´dx, причем единичный размер много меньше ширины зазора b.
Если давление, действующее на левую грань выделенного объема, обозначить через р, то на правую грань будет действовать давление

На верхнюю и нижнюю грани будут действовать касательные напряжения, равные

и направленные в сторону, противоположную движению.
На передней и задней гранях касательные напряжения равны нулю потому, что в направлении, нормальном к плоскости хоу скорость не меняется, а следовательно, и нет градиента скорости.

Рис. 4.11. Ламинарное течение с переменной вязкостью
Поэтому уравнение равновесия выделенного объема запишется в виде

или

Следует иметь в виду, что здесь обе производные отрицательны, так как положительным приращениям dx и dy соответствуют отрицательные приращения dp и dv.
Интегрируя уравнение в пределах поперечного сечения потока, а потому считая dp/dx и m величинами постоянными, получим

Так как при у=а V/2=0, то

и, следовательно,

| (4.22) |
Определим расход, приходящийся на единицу ширины зазора, для чего поступим аналогично тому, как это делалось в предыдущем параграфе. Используя (4.22), будем иметь

| (4.23) |
При этом, если Q=const (жидкость абсолютно несжимаема), то одно переменное пропорционально другому.
Запишем теперь уравнение энергии, т.е. равенство между потерей энергии на трение, перешедшей в тепло, и приростом тепловой энергии жидкости за единицу времени:

| (4.24) |
Здесь с - теплоемкость жидкости в системе единиц СИ, т.е. в дж/кг град; р - давление в н/м2; k - коэффициент, учитывающий долю работы сил вязкости, которая идет на нагревание жидкости.
При k=1 отсутствует теплоотдача через стенку, и вся работа сил вязкости идет на нагревание жидкости. При k=0 происходит интенсивная теплоотдача через стенку, а повышения температуры жидкости не происходит (изотермическое течение).
Из предыдущего имеем

что после подстановки в выражение (4.21) дает

| (4.25) |
Используем полученную связь между m и p (4.25) для интегрирования уравнения (4.23).
После разделения переменных вместо (4.23) будем иметь

или

После интегрирования получим

Постоянную интегрирования находим из условий в начальном сечении потока, где при х=0 р=р1, следовательно,

В конечном сечении потока при х=l р=ризб=0. Поэтому окончательно получим

| (4.26) |
Следует иметь в виду, что входящая сюда величина m1 - это вязкость в начальном сечении потока, т.е, при р=р 1 и t=to она может быть выражена через mо - вязкость при р=ризб=0 и t=to, по формуле (4.21)

| (4.27) |
В частном случае изотермического течения в формуле (4.26) следует положить k=0. С учетом предыдущего в этом случае получим

| (4.28) |
Найдем относительный расход Qo, равный отношению расхода при переменной вязкости к расходу при m=mо=const. Для этого разделим уравнение (4.26) на

Будем иметь
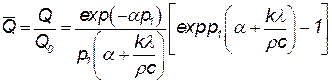
| (4.29) |
По формуле (6.24) произведены подсчеты для ряда значений давления р1 от 0 до 800 кГ/см2 (7840 н/см2) при следующих значениях констант: a=1/430 см2/кГ (1/4210 см2/н); l=1/36 1/град; с=2,1 кдж/кг град (0,5 ккал/кг град); g=850 кГ/м3 (8330 н/м3).
Результаты подсчетов представлены на рис. 55 в виде кривых зависимости Q от р1 для двух значений k: k=1 (отсутствие теплообмена) и k=0 (изотермическое течение).
Как видно из графика, кривые, соответствующие двум крайним режимам, расходятся довольно существенно. Реальные процессы отображаются кривыми, которые располагаются между этими предельными кривыми. В связи с тем, что скорости течения жидкости в зазорах при столь высоких перепадах давления очень велики и пребывание каждой частицы в зазоре является весьма кратковременным, более вероятным представляется режим течения, при котором k→0, т.е. теплообмен играет малую роль.
Однако следует иметь в виду, что при увеличении относительной длины зазора l/а, числа Рейнольдса и числа Прандтля, равного

(с - теплоемкость, l - коэффициент теплопроводности), роль теплообмена возрастает и процесс течения может приблизиться к изотермическому.
Из предыдущих выражений можно легко получить формулу, связывающую между собой относительную координату х/l и давления р и р1.
Задаваясь различными значениями р при постоянном р 1 можно подсчитать соответствующие значения х/l и построить эпюру давления вдоль зазора для ряда постоянных значений давления в начале зазора р1.

Рис. 4.12. Влияние вязкости на расход жидкости
Результаты такого рода расчетов представлены на рис. 4.13 в виде зависимостей р/р1 от х/l для трех постоянных р1 при k=1.

Рис. 4.13. Эпюра давления в зазоре учетом переменной вязкости и плотности жидкости